Работа 3. затухающие квазигармонические колебания
В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ.
ЦЕЛЬ РАБОТЫ
1.Ознакомиться с осциллографическим методом изучения колебательных процессов.
2.Определить основные характеристики колебаний.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.
Электрическая цепь, обладающая индуктивностью L и емкостью С и не обладающая активным сопротивлением, является идеальным колебательным контуром. Если такому контуру сообщить энергию, то в нем возникают гармонические колебания электрических величин: заряда, напряжения, силы тока с периодом
Tо= 2 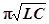 (15)
(15)
или циклической частотой 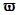 = (
= ( 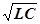 )-1
)-1
Колебания в контуре сопровождаются взаимными превращениями электрического и магнитного полей.
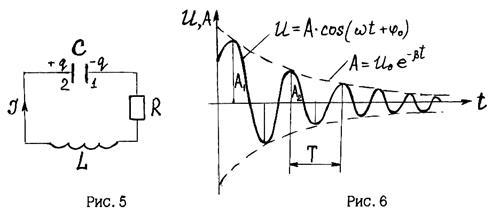
Всякий реальный контур (рис.5) обладает активным сопротивлением R. В этом случае электромагнитная энергия контура постепенно расходуется на преодоление сопротивления и, превращаясь во внутреннюю энергию контура, нагревает его, вследствие чего колебания с течением времени затухают.
Найдем уравнение колебаний в контуре CLR. Напишем для цепи 1-3-2 (рис.5) выражение закона Ома (см. раб.1):
IR = j1 - j2 + e (16)
Пусть в данный момент величина заряда на обкладках конденсатора равна q. Условимся считать положительным ток, заряжающий конденсатор.
Тогда I= 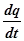 =
= 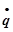
 j1 - j2 =
j1 - j2 = 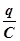
1. e1 - e2 = -L (d 2q /dt2 ) = -L 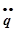 ; эдс цепи – эдс самоиндукции
; эдс цепи – эдс самоиндукции
Подстановка этих выражений в (16) дает L 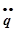 + R
+ R 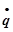 +
+ 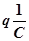
Разделим это уравнение на L и введем обозначения:
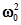 =
= 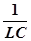 ;
; 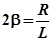
где: 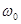 - собственная частота колебательного контура (при R=0),
- собственная частота колебательного контура (при R=0),
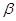 - коэффициент затухания.
- коэффициент затухания.
Получим уравнение изменения заряда на обкладках конденсатора:
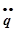 + 2
+ 2 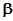
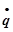 +
+ 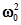 q = 0 (17)
q = 0 (17)
По такому же закону изменяется напряжение на обкладках конденсатора:
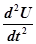 + 2b
+ 2b 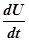 +
+ 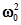
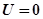 (18)
(18)
Уравнения (17) и (18) носят название дифференциальных уравнений затухающих колебаний.
Затухание нарушает периодичность колебаний, поэтому, строго говоря, к ним неприменимо понятие периода или частоты. 
Однако в случае малых затуханий ( 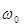 >>
>> 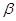 ) можно условно пользоваться понятием периода как промежутка времени между двумя последовательными максимумами ( или минимумами ) колеблющейся физической величины. Такие колебания называются квазигармоническими .Решение уравнения (18) в этом случае имеет вид:
) можно условно пользоваться понятием периода как промежутка времени между двумя последовательными максимумами ( или минимумами ) колеблющейся физической величины. Такие колебания называются квазигармоническими .Решение уравнения (18) в этом случае имеет вид:

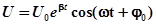 (19)
(19)
где: 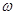 =
= 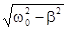 - частота свободных квазигармонических колебаний,
- частота свободных квазигармонических колебаний,
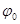 - начальная фаза,
- начальная фаза, 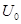 - значение амплитуды в момент времени t = 0.
- значение амплитуды в момент времени t = 0.
Период колебаний определяется формулой:
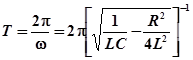 (20)
(20)
При R = 0 формула (20) переходит в формулу (15).
Из (16) видно, что амплитуда затухающих колебаний с течением времени убывает по экспоненциальному закону:
A = 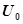 e
e 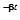 =
= 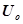 e
e 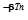
 (21)
(21)
где n - число периодов, содержащихся в промежутке времени t .  Графики функций (19) и (21) изображены на рис.6.
Графики функций (19) и (21) изображены на рис.6. 
В качестве меры затухания колебаний на практике чаще применяют не коэффициент затухания , а связанн  ый с ним логарифмический декремент затухания
ый с ним логарифмический декремент затухания 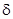 , который bопределяется как натуральный логарифм отношения двух амплитуд, разделенных во времени на один период
, который bопределяется как натуральный логарифм отношения двух амплитуд, разделенных во времени на один период
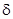 =
= 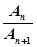 (22)
(22)
Выразив 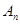 и
и 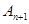 по формуле (21), можно получить соотношение
по формуле (21), можно получить соотношение

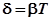
Логарифмический декремент 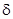 - постоянная для данного контура величина.
- постоянная для данного контура величина.
Для характеристики колебательного контура пользуются также понятием добротности Q , которая пропорциональна отношению энергии, запасенной в контуре в данный момент, к убыли этой энергии за один период колебаний
Q = 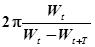 и Q =
и Q = 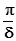 (23)
(23)
Чем меньше затухание, тем больше добротность Q.
При условии 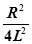 =
= 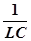 , т.е. при
, т.е. при 
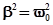 (24)
(24)
выражение (20) обращается в бесконечность. Сопротивление контура, соответствующее условию (24), называется критическим Rкр.:
Rкр.= 2 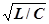 (25)
(25)
Начиная с этого значения R  Rкр, процесс в контуре будет апериодическим.
Rкр, процесс в контуре будет апериодическим.
ОПИСАНИЕ УСТАНОВКИ
 Схема установки приведена на рис.7. Магазин емкости Р5025,катушка индуктивности и магазин сопротивлений Р4830/1 образуют колебательный контур CLR . Возбуждение колебаний в контуре осуществляется с помощью мультивибратора МВ, собранного на двойном триоде 6Н8С, питание от источника ВУП-2М.
Схема установки приведена на рис.7. Магазин емкости Р5025,катушка индуктивности и магазин сопротивлений Р4830/1 образуют колебательный контур CLR . Возбуждение колебаний в контуре осуществляется с помощью мультивибратора МВ, собранного на двойном триоде 6Н8С, питание от источника ВУП-2М.
Рис.7
На экране осциллографа С1-55 наблюдают колебания напряжения во времени. Рекомендуются следующие положения управляющих рукояток осциллографа:
СИНХРОНИЗАЦИЯ – внешняя
УСИЛИТЕЛЬ У1 0,02 или 0,05 В/дел
РАЗВЕРТКА длительность 0,2 - 0,5 ms/дел
множитель развертки х 1
Положение рукоятки "длительность“ определяет цену большого деления горизонтальной оси экрана осциллографа  t , положение рукоятки усилителя У1 указывает цену большого деления вертикальной оси напряжения.
t , положение рукоятки усилителя У1 указывает цену большого деления вертикальной оси напряжения.
При измерении периода колебаний центральная часть ручки "длительность" должна быть повернута по часовой стрелке до щелчка. Устойчивая картина на экране получается с помощью ручек "Стаб.", "Уровень". Счет числа колебаний необходимо начинать с максимума первого положительного полупериода, считая его нулевым.
Для определения критического сопротивления необходимо добиться картины, показанной на рис.8, причем участок DЕ должен быть плавным при минимальном сопротивлении магазина. Участок АВСD обусловлен возбуждающим импульсом и переходными процессами.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Включите питание осциллографа и источника ВУП-2М. После прогревания на экране осциллографа должна появиться четкая картина затухающего импульса, положение которой можно менять с помощью ручек "  " и "
" и "  ".
".
ЗАДАНИЕ 1. Определение периода и частоты колебаний.
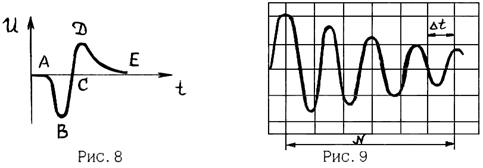
а) Используя масштабную сетку экрана осциллографа (рис 9),рассчитать период и циклическую частоту по формулам:
Т = 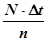 ;
; 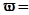
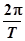 ;
;
где: N - число делений горизонтальной оси, соответствующее целому числу периодов n,
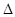 t - цена деления горизонтальной оси.
t - цена деления горизонтальной оси.
Для случая, изображенного на рис.9 N=6 n=4
б) По параметрам контура С, L и R рассчитайте период и циклическую частоту по формулам (20).Сравните значения Т и  , полученные в пунктах а) и б).
, полученные в пунктах а) и б).
ЗАДАНИЕ 2. Определение закона спадания амплитуды, определение 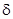 и Q.
и Q.
Измерьте последовательные амплитуды А 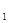 ,А
,А 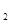 ,....,А
,....,А 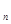 ,не менее 6 амплитуд. Для уменьшения погрешности желательно их измерять в одном и том же месте экрана, перемещая кривую по горизонтали.
,не менее 6 амплитуд. Для уменьшения погрешности желательно их измерять в одном и том же месте экрана, перемещая кривую по горизонтали.
Экспоненциальный характер закона спадания амплитуды подтверждается тем, что зависимость ln А от n имеет линейный характер. Действительно, прологарифмировав (21), получим
ln A = ln Uo - 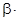 T n или y = ax + b ,
T n или y = ax + b ,
где b = ln Uo , a = - 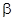 T = -
T = - 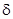 , y = ln A , x = n .
, y = ln A , x = n .
Постройте график ln A = f (n) и убедитесь, что график-прямая линия.
Значение коэффициента а для этого графика a = tg 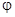 =
= 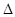 lnA /
lnA / 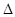 n
n
где: 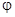 - угол наклона прямой к горизонтальной оси x. Следовательно, логарифмический декремент ,равный коэффициенту a ,можно найти по графику ln A = f (n) .
- угол наклона прямой к горизонтальной оси x. Следовательно, логарифмический декремент ,равный коэффициенту a ,можно найти по графику ln A = f (n) .
Рассчитайте значение 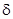 по формуле (22) и сравните его со значением, полученным по графику.
по формуле (22) и сравните его со значением, полученным по графику.
Рассчитайте добротность контура Q по формуле (23).
ЗАДАНИЕ 3. Изучение влияния емкости, индуктивности и сопротивления (качественно) на характеристики затухающих колебаний.
Для этой цели последовательно меняйте емкость магазина емкостей С, индуктивность L (катушка без сердечника, с сердечником), сопротивление R, возвращаясь к начальным параметрам. Пронаблюдайте, как изменяется при этом период (частота) колебаний и интенсивность затухания.
Зарисуйте наблюдаемые кривые и дайте объяснения различиям с позиции теории.
Меняя сопротивление контура, добейтесь перехода процесса от гармонического к апериодическому. Полученное значение R кр., равное сумме сопротивлений магазина и катушки, запишите. Сравните со значением, полученным по формуле (25).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое колебания? свободные колебания ? гармонические колебания? квазигармонические
колебания? периодические процессы ?
2. Дайте определения амплитуды, фазы, периода, частоты, циклической частоты колебания ?
3. Запишите формулу периода колебаний а) для идеального контура и б) для колебательного контура с сопротивлением R.
4. Запишите дифференциальное уравнение затухающих электромагнитных колебаний и его решение.
5. По какому закону изменяется амплитуда затухающих колебаний?
6. Что такое логарифмический декремент затухания колебательной системы ? коэффициент затухания ?
7. Запишите соотношение между частотой затухающих колебаний и собственной частотой. При каких условиях наблюдается апериодический процесс в колебательном контуре?
ЛИТЕРАТУРА:[ 2. § 90]
РАБОТА 4. ИЗУЧЕНИЕ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ МЕТАЛЛОВ
ОТ ТЕМПЕРАТУРЫ.
ЦЕЛЬ РАБОТЫ
1. Провести исследование температурной зависимости сопротивления металлического проводника.
2. Определить значение температурного коэффициента a и сопротивления Ro. 
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Металлы относятся к проводникам первого рода, прохождение тока в них не сопровождается переносом вещества (атомов, ионов). Ток проводимости в металлах представляет собой обусловленный электрическим полем медленный систематический дрейф свободных электронов, наложенный на их хаотическое тепловое движение.
Установление постоянной скорости дрейфа (постоянный электрический ток) означает появление сил, тормозящих движение электронов и уравновешивающих электрические силы. Эти силы сопротивления вызываются взаимодействием зарядов друг с другом и с кристаллической решеткой.
Одно из фундаментальных утверждений физики твердого тела состоит в том, что на движение электронов не влияет их взаимодействие с идеальной решеткой. Если решетка не идеальна, то это
приводит к рассеянию электронов, т.е. к появлению сопротивления. Неидеальность решетки связана, во-первых, с колебаниями узлов кристаллической решетки – положительных ионов металла вследствие хаотического теплового движения, во-вторых, с дефектами решетки. Различают: точечные дефекты – вакантные узлы, ионы примесей в узлах решетки, внедренные атомы примесей в междоузлиях, линейные дефекты-дислокации и объемные дефекты-границы
кристаллитов.
Рассеяние электронов вследствие искажения решетки хаотическим тепловым движением носит название фононного; значение удельного сопротивления, обусловленное этой причиной, обозначим 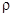 ф. Рассеяние электронов на дефектах решетки называют примесным, значение удельного сопротивления, обусловленное этой причиной, обозначим rпр. В неупорядоченных сплавах даже при комнатной температуре доминирующей причиной, обуславливающей сопротивление, являются дефекты решетки, тогда как в чистых металлах основной причиной сопротивления является тепловое движение.
ф. Рассеяние электронов на дефектах решетки называют примесным, значение удельного сопротивления, обусловленное этой причиной, обозначим rпр. В неупорядоченных сплавах даже при комнатной температуре доминирующей причиной, обуславливающей сопротивление, являются дефекты решетки, тогда как в чистых металлах основной причиной сопротивления является тепловое движение.
Матиссен (1867 г.) установил, что полное удельное сопротивление 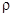 складывается аддитивно из этих двух составляющих:
складывается аддитивно из этих двух составляющих:
 =
= 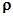 ф +
ф + 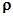 пр
пр
Для чистых металлов и металлов с примесями при температурах, близких к комнатной, сопротивление с увеличением температуры растет линейно:
R = R0 ( 1 + 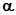 t ) =
t ) = 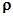 0
0 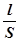 (1 +
(1 + 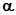 t ) (26)
t ) (26)
где 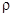 0 - удельное сопротивление проводника при t = 00 С,
0 - удельное сопротивление проводника при t = 00 С,
 - температурный коэффициент сопротивления,
- температурный коэффициент сопротивления,
l и S - длина и площадь поперечного сечения проводника.
В области низких температур зависимость сопротивления от температуры может быть очень сложной.
ОПИСАНИЕ УСТАНОВКИ
Схема установки представлена на рис.10. Исследуемый образец 1 помещается в термостат 2. Температура в термостате измеряется термометром 3, задается положением реостата 5.
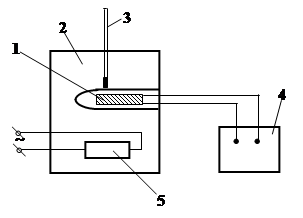
Сопротивление образца определяется
прибором 4, в качестве которого могут
использоваться: мост сопротивления
МО-62, цифровой измеритель Р 5030,
универсальный вольтметр В7-16 А
или осциллограф мультиметр С1-112.
Рис.10
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Провести измерения сопротивления металлического проводника при комнатной температуре
и выше через 4-5 градусов. Результаты измерений (не менее 10 пар точек) оформить в виде таб-
лицы.
2. По экспериментальным данным построить график зависимости сопротивления от температуры.
3. Значения температурного коэффициента  и сопротивления R0 при температуре 00 С могут
и сопротивления R0 при температуре 00 С могут
быть найдены по графику и из формулы (26), которую можно привести к виду: y = ax + b ,
где а = Ro  , b = Ro , y = R , x = t .
, b = Ro , y = R , x = t .
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какова связь между сопротивлением и удельным сопротивлением, между удельным
сопротивлением и удельной проводимостью? Каковы их единицы измерения?
2. Объясните механизм возникновения сопротивления в металлах.
3.Удельное сопротивление сплава двух металлов почти всегда больше, чем каждого из них в
отдельности. Как это объяснить?
4. Какова температурная зависимость сопротивления металлов?
5. Каков физический смысл температурного коэффициента сопротивления? Как он определяется в
данной работе?
6. Как по графику температурной зависимости сопротивления определить Ro?
7. В чем заключается явление сверхпроводимости?
ЛИТЕРАТУРА: [4]
