Дифференциальное уравнение свободных колебаний

Для изучения любого физического явления необходима модель. Моделью для изучения механических колебаний является гармонический осциллятор.

Гармоническим осциллятором называется система, совершающая колебания, которые могут быть описаны дифференциальным уравнением свободных гармонических колебаний, имеющим вид:

. (19.5)

Выражение (19.5) является линейным однородным дифференциальным уравнением второго порядка. Согласно общей теории линейных дифференциальных уравнений, решением уравнения (19.5) является выражение (19.1).

Колебания гармонического осциллятора являются важным примером периодического движения. Примерами гармонического осциллятора являются пружинный, математический и физический маятники.

Пружинный маятник - Пружинный маятник тело, подвешенное на пружине жесткостью k.Модель пружинного маятника показана на рис.19.1. Положение тела, при котором пружина не деформирована, является положением устойчивого равновесия. При отклонении тела от положения равновесия в результате деформации возникает сила упругости, которая согласно закону Гука равна .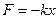

Свободные колебания совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Рис. 19.1

В случае пружинного маятника уравнение движения согласно второму закону Ньютона можно записать . Делим на m, получим:

. (19.6)

Учтем, что 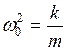, получим уравнение (19.5)

Период колебаний пружинного маятника определяется как

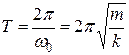. (19.7)

Потенциальная энергия пружинного маятника определяется как:

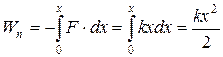. (19.8)

Математический маятник. Математическим маятником называют подвешенный на тонкой нерастяжимой нити груз, размеры которого меньше длины нити, а масса больше массы нити.

Положение, в котором нить вертикальна – положение устойчивого равновесия. В положении устойчивого равновесия сила тяжести 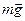уравновешена силой натяжения нити , как показано на рис.19.2. При отклонении нити на угол α торавнодействующая сил тяжести и силы натяжения нити будет направлена к положению устойчивого равновесия.

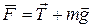. (19.9)

Если тело отпустить, то будем наблюдать свободные колебания. Во время колебаний можно считать, что меняется только координата х. Запишем проекцию равнодействующей силы на ось х

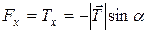. (19.10)

При малых значениях a (a ~4^о) пренебрегаем движением вдоль оси y

(19.11)

Рис.19.2.

Из уравнения (19.10), учитывая (19.11) определим проекцию равнодействующей силы на ось х, которая согласно второму закону Ньютона равна

,

учтем, что 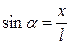, получим

Уравнение гармонических колебаний математического маятника можно записать в дифференциальной форме

. (19.12)

Подставим значение . Получим уравнение (19.5). Отсюда период математического маятника равен

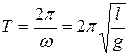, (19.13)

где l – длина математического маятника.

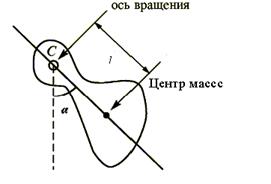
Физический маятник. Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, не проходящей через центр масс. Ось вращения, которого, расположена выше центра масс (рис.19.3).

При колебаниях физического маятника, возникает вращающий момент 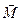, который согласно основному уравнению динамики вращательного движения равен:

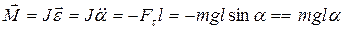, (19.14)

где J – момент инерции,

ε – угловое ускорение,

l – расстояние между точкой подвеса и центром масс. Уравнение (19.14) можно записать в виде: 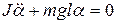или .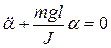

Принимая во внимание или .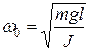

Можно получить выражение периода колебаний физического маятника:

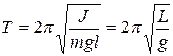, (19.15)

где 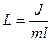- приведенная длина физического маятника. Приведенная длина, приравнивается длине математического маятника с таким же периодом колебаний.

Рис.19.3.

Период колебаний физического маятника, следовательно, и его приведенная длина, немонотонно зависят от расстояния от точки подвеса до центра масс маятника. Это легко заметить, если в соответствии с теоремой Штейнера (4.7) момент инерции выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс. Тогда период колебаний будет равен

, (19.16)

где J₀ –момент инерции центра масс.

На практике значения низших собственных частот систем могут быть весьма малыми. Например, бельевая веревка, подвешенная на двух столбах, может в случае достаточного провисания совершать свободные колебания с частотой 1-2Гц. Колебания такого типа были обнаружены осенью 1959г. у проводов линии электропередачи, пересекавшей реку Северную, частота собственных колебаний была весьма низкой - около 1/8Гц. Провода диаметром 43мм, протянутые над рекой, были прикреплены к двум большим пилонам, расстояние между которыми превышало 1,6км. Было обнаружено, что когда ветер дул с небольшой силой, но в определенном направлении, возникали столь интенсивные низкочастотные колебания проводов, что эти провода, минимальное расстояние между которыми составляло 8,2м, входили в соприкосновение, вызывавшее короткое замыкание в системе электропередачи. (Была найдена вероятная причина этих колебаний, и в дальнейшем их удалось предотвращать путем покрытия тросов тонкой пластиковой лентой: благодаря этому изменялась геометрия поверхности, обтекаемой воздушным потоком).

Колебания проводов над рекой не представляют собой свободных колебаний, поскольку в этом случае пассивная система находилась под действием внешнего источника энергии - ветра. Однако характерно, что при решении этой проблемы инженерам, как обычно, потребовалась информация относительно значений собственных частот системы, близких к частоте наблюдавшихся колебаний.

18.3.Скорость и ускорение гармонических колебаний

Если материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат тогда зависимость координаты х от времени t описывается уравнением (19.1). Скорость и ускорение a колеблющееся точки соответственно равны:

, (19.17)

и , (19.18)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды скорости и ускоренияколебаний соответственно равны υ_max = Аw и a_max= Аw₀². Фаза скорости (19.17) отличается от фазы величины (19.1) на 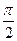, а фаза ускорения (19.18) отличается от фазы величины (19.1) на 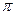. В момент времени, когда х=0скорость колеблющейся точки максимальна по величине и равна амплитуде скорости в моменты прохождения колеблющейся точки через положение равновесия. При максимальных смещениях (х =±А) скорость равна нулю. Вектор скорости всегда направлен в сторону движения.

Ускорение равно нулю при прохождении колеблющейся точки через положение равновесия и достигает максимального по величине значения, которое равно амплитуде ускорения, при максимальных смещениях колеблющейся точки. Вектор ускорения всегда направлен в сторону положения равновесия. Удаляясь от положения равновесия, колеблющаяся точка движется, замедлено, приближаясь к нему – ускоренно.

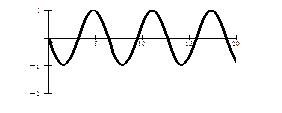Рис.19.4.

График гармонического колебания, который описывается уравнением (19.1), скорость гармонического колебания, описываемая уравнением (19.17), и ускорение (19.18) показаны на рис.19.4. Видно, что смещение, скорость и ускорение гармонически колеблющейся точки являются периодическими функциями от времени с одинаковыми периодами.

Энергия колебаний