Закон Ома. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения на проводнике:
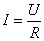 . . | (3.1) |
Под однородностью понимается отсутствие сторонних сил.Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении в 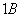 течет ток силой в
течет ток силой в 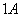 . Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
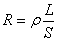 , , | (3.2) |
где 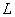 – длина проводника,
– длина проводника,  – площадь поперечного сечения,
– площадь поперечного сечения, 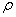 – зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. Удельное сопротивление численно равно сопротивлению единицы длины проводника, имеющего площадь поперечного сечения, равную единице.
– зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. Удельное сопротивление численно равно сопротивлению единицы длины проводника, имеющего площадь поперечного сечения, равную единице.
 Рис. 3.2 Рис. 3.2 |
В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора напряженности электрического поля 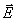 . Поэтому направления векторов
. Поэтому направления векторов 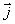 и
и 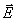 совпадают. Найдем связь между
совпадают. Найдем связь между 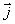 и
и 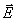 в одной и той же точке проводника. Для этого выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам
в одной и той же точке проводника. Для этого выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам 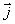 и
и 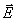 (рис. 3.2). Через поперечное сечение цилиндра течет ток силой
(рис. 3.2). Через поперечное сечение цилиндра течет ток силой 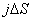 . Так как поле внутри выделенного объема можно считать однородным, то напряжение, приложенное к цилиндру, равно
. Так как поле внутри выделенного объема можно считать однородным, то напряжение, приложенное к цилиндру, равно 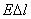 , где
, где 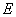 – напряженность поля в данном месте. Сопротивление цилиндра, согласно (3.2), равно
– напряженность поля в данном месте. Сопротивление цилиндра, согласно (3.2), равно 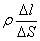 . Подставив эти значения в формулу (3.1), придем к соотношению:
. Подставив эти значения в формулу (3.1), придем к соотношению:
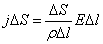 ,
,
откуда
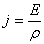 .
.
Воспользовавшись тем, что векторы 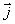 и
и 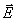 имеют одинаковое направление, можно написать
имеют одинаковое направление, можно написать
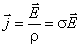 . . | (3.3) |
Величина 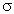 называетсяудельной электрической проводимостью материала. Единицей измерения
называетсяудельной электрической проводимостью материала. Единицей измерения 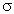 является сименс. Формула (3.3) дает выражение закона Ома в дифференциальной форме, это означает, что она связывает величины, относящиеся к одной точке пространства.
является сименс. Формула (3.3) дает выражение закона Ома в дифференциальной форме, это означает, что она связывает величины, относящиеся к одной точке пространства.
Для участка цепи, на котором действуют сторонние силы, закон Ома запишется в следующей форме:
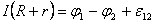 . . | (3.4) |
Перепишем (3.4) в виде
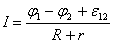 .
.
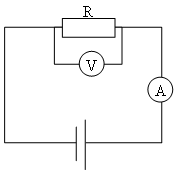 Рис. 3.3 Рис. 3.3 |
Эта формула выражает закон Ома для неоднородного участка цепи.
Рассмотрим простейшую замкнутую цепь, содержащую источник тока и нагрузку с сопротивлением R (рис. 3.3). Сопротивлением подводящих проводов пренебрегаем. Положив 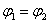 , получим выражение закона Ома для замкнутой цепи:
, получим выражение закона Ома для замкнутой цепи:
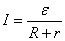 .
.
Идеальный вольтметр, подключенный к зажимам работающего источника тока, показывает напряжение 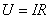 , как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. Подставляя силу тока из этого выражения в закон Ома для замкнутой цепи, получаем:
, как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. Подставляя силу тока из этого выражения в закон Ома для замкнутой цепи, получаем:
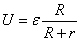 .
.
Отсюда видно, что напряжение U на зажимах работающего источника всегда меньше его ЭДС. Оно тем ближе к 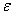 , чем больше сопротивление нагрузки R. В пределе при
, чем больше сопротивление нагрузки R. В пределе при 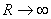 напряжение на зажимах разомкнутого источника равно его ЭДС. В противоположном случае, когда R=0, что соответствует короткому замыканию источника тока, U=0, а ток при коротком замыкании максимален:
напряжение на зажимах разомкнутого источника равно его ЭДС. В противоположном случае, когда R=0, что соответствует короткому замыканию источника тока, U=0, а ток при коротком замыкании максимален: 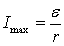 .
.
Закон Ома позволяет рассчитать любую сложную цепь. Разветвленная цепь характеризуется силой токов, идущих по ее участкам, сопротивлениями участков и ЭДС, включенными в эти участки. Сила тока и ЭДС являются величинами алгебраическими, то есть считаются положительными, если электродвижущая сила способствует движению положительных зарядов в выбранном направлении, а ток течет в этом направлении, и отрицательными в противоположном случае. Однако непосредственный расчет разветвленных цепей бывает сложным. Этот расчет значительно упрощается при использовании правил, предложенных Кирхгофом.
