Обробка результатів експерименту та їх аналіз

1. Знайти середні значення радіусів окремих темних кілець Ньютона r₅, r₇, r_11, якщо кожне з них вимірювалось по кілька разів.

2. Обчислити довжину хвилі за формулою (8).

3. Знайти похибки вимірювань.

4. Результати обчислень занести в таблицю.

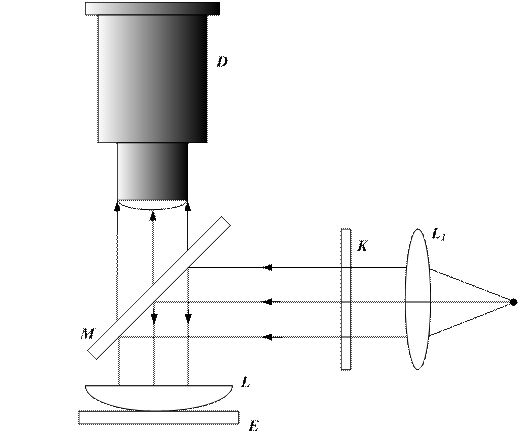
Рис. 3

Дослідницьке завдання

Розглянути інтерференційну картину, якщо проміжок між лінзою та пластиною заповнений рідиною.

Контрольні запитання для допуску

До виконання лабораторної роботи

1. Мета роботи.

2. Як практично в лабораторній роботі отримують кільця Ньютона?

3. Що таке інтерференція? Які промені інтерферують в системі кільця Ньютона?

4. Чи є різниця між відбитим променем на межі з оптично більш густим середовищем і відбитим променем на межі з оптично менш густим середовищем?

5. Проведіть виведення радіуса темного кільця Ньютона.

6. Проведіть виведення радіуса світлого кільця Ньютона.

7. Чи залежить радіус будь-якого кільця Ньютона від радіуса кривизни опуклої лінзи?

8. Чому для вимірювання радіуса кривизни кілець Ньютона слід використовувати світлофільтр?

9. Як пояснити той факт, що в центрі інтерференційної картини завжди спостерігається мінімум?

Контрольні запитання для захисту лабораторної роботи

1. Чому для одержання задовільних результатів не слід вимірювати радіуси сусідніх кілець Ньютона?

2. Які фактори впливають на точність вимірювання довжини хвилі в даній лабораторній роботі?

3. Чи зміниться картина інтерференції, якщо простір між лінзою і скляною пластинкою заповнити водою?

4. Навести приклади практичного використання явища інтерференції світла?

5. Чому ширина кілець Ньютона зменшується із збільшенням їх радіуса?

Лабораторна робота № 5.6

Визначення довжини світлової

Хвилі за допомогою дифракційної решітки

Мета роботи:вивчити явище дифракції на щілині і дифракційній решітці; освоїти методику визначення довжини світлової хвилі за допомогою дифракційної решітки.

Прилади і матеріали:гоніометр, дифракційна решітка, джерело світла.

Теоретичні відомості

Явище дифракції світла полягає у відхиленні світлових хвиль від прямолінійного напрямку при проходженні світла через малі отвори або біля малих перешкод. Дифракція світлових хвиль спостерігається, якщо розміри отворів або перешкод одного порядку з довжиною світлової хвилі, або якщо місце для спостереження дифракційної картини знаходиться на великій відстані від отвору або перешкоди.

Нехай паралельний пучок монохроматичного світла падає нормально на непрозорий екран, в якому є вузька щілина довжиною l і постійної ширини b, причому b << l (рис. 1). Згідно з принципом Гюйгенса-Френеля точки щілини є джерелами вторинних хвиль. Фази цих хвиль будуть однакові, оскільки площина щілин збігається з фронтом хвилі, що падає.

Оскільки закон прямолінійного поширення світла порушується, у фокальній площині збиральної лінзи буде спостерігатися розподіл інтенсивності дифрагованих променів. У побічному фокусі F_φцієї лінзи зберуться всі промені, кут дифракції яких дорівнює φ. Оптична різниця ходу крайніх променів АМ і ВN, щойдуть від щілини в цьому напрямі, а різниця фаз цих коливань

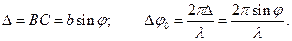(1)

Знайдемо амплітуду результуючого коливання, що йде від щілини в точку F_φ. Для цього подумки розділимо щілину на велике число дуже вузьких прямокутних зон і графічно складемо вектори амплітуд коливань від кожної з цих зон. Всі зони будуть випромінювати в заданому напрямі зовсім однаково.

Тому вектори амплітуд будуть мати однакові значення, а різниця фаз двох коливань від сусідніх зон буде постійною. У ньому випадку одержуємо ламану лінію, яка є частиною правильного багатокутника. При нескінченному зростанні числа зон ця ламана переходить в частину дуги кола (рис.2).

Рис. 1

З рис. 2 маємо:

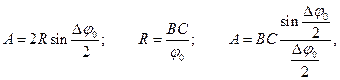(2)

де ВС ­– інтервал дуги.

При Δφ₀ = 0; А₀ = ВС, тому співвідношення (2) можна записати у такому вигляді:

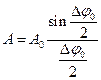. (3)

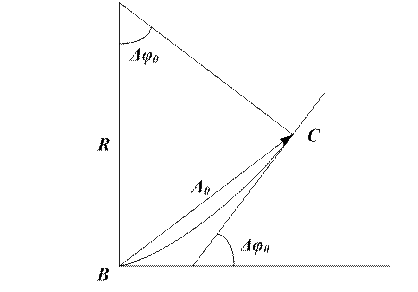
Рис. 2

Інтенсивність світлових хвиль можна визначити за формулою

. (4)

Функція f(∆φ₀) носить назву фактора розсіювання і характеризує вплив щілини на дифракцію світлових променів.

Мінімум буде спостерігатися в тому випадку, коли 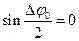, але .

Тоді ;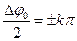

;

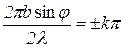або

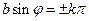. (5)

Максимуми будуть спостерігати там, де 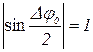, а також при і при (центральний максимум).

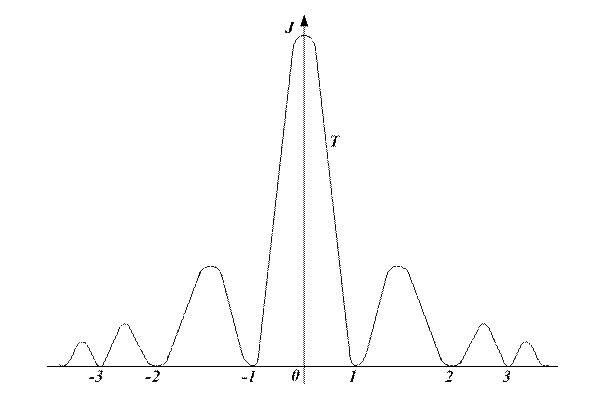
Рис. 3

Тому

,

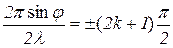або

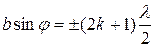. (6)

Формула (6) визначає положення побічних максимумів. Схематичне зображення розподілу інтенсивності світла в дифракційній картині на щілині (функція f(∆φ ₀)) показано на рис. 3.

Розглянемо дифракцію на дифракційній решітці. Дифракційна решітка – це прозора пластинка, на якій за допомогою ділильної машини або фотографічним способом нанесені паралельно один одному штрихи і залишені вузькі непошкоджені смужки. Ті місця, де проведені штрихи, непрозорі і служать перешкодами для світлових хвиль.

Нехай ширина прозорої смужки а, а ширина штриха b. Величину d = а + b прийнято називати періодом решітки або постійною решітки (рис.4).

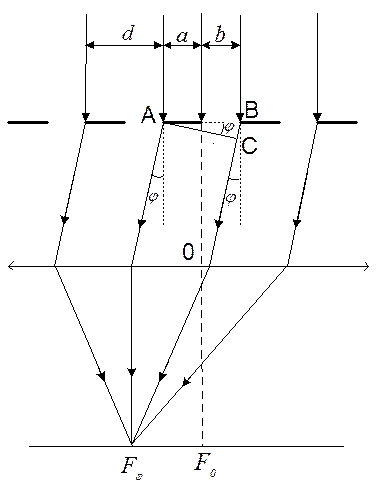
Рис.4

Знайдемо результуючу інтенсивність світлових хвиль в точці F_φ, в якій збираються промені від всіх щілин решітки, що падають на лінзу під кутом φ до її головної оптичної осі ОF₀ . Скористаємося для цього векторною діаграмою додавання амплітуд:

, (7)

де N - число щілин у решітці,

А_i - вектор амплітуди коливань, що викликаються у даній точці дією і -ї щілини.

У випадку оптичної однорідності середовища в одному і тому напрямі всі щілини випромінюють світло однаково.

Тому всі вектори А_і однакові за модулем . Зсув фаз Δφ₀ між векторами Δ визначається оптичною різницею ходу Δ від відповідних точок двох сусідніх щілин до точки F_φ. Тому

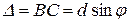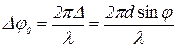; (8)

Таким чином, виникла задача додавання N хвиль, що описуються рівнянням

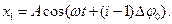(9)

Скористаємося графічним методом розрахунку. У результаті додавання векторів амплітуд , одержимо результат, показаний на рис. 5. Вершини цього багатокутника лежать на колі (переконатися в цьому самостійно). Знайдемо радіус кола. Нехай точка С є центром шуканого кола. Тоді 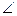OCB дорівнює різниці фаз ∆φ₀ .

Отже,

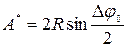. (10)

Центральний кут α, на який опирається амплітуда А, дорівнює

α = .

З урахуванням цього кута амплітуда А буде дорівнювати:

. (11)

Поділимо співвідношення (11) на (10), одержимо:

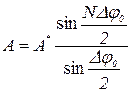, (12)

а з урахуванням співвідношень (8) одержимо остаточно:

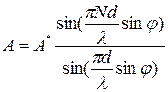. (13)

Проведемо дослідження одержаного виразу для амплітуди результуючих коливань.

Якщо , то .

Розкриваючи невизначеність за правилом Лопіталя, знайдемо

,

тобто

.

Таким чином, у цьому випадку спостерігається максимум дифракційної картини. Його називають максимумом нульового порядку (або нульовим).

Знайдемо умову головних максимумів дифракційної решітки:

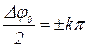(k = 0,1,2, … ) .

Звідси

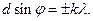(14)

формула (14) є умовою головних максимумів решітки.

Побічні мінімуми будуть спостерігатись, якщо А=0. Це можливо при умові, коли

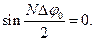
або

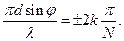
Звідси одержуємо

або

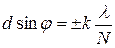– побічні мінімуми, (15)

де k приймає довільні цілі значення, крім 0; N; 2N; 3N ...

З формули (14) видно, що положення дифракційних максимумів залежить від довжини хвиль. Іншими словами, дифракційна решітка є спектральним приладом.

Основними оптичними характеристиками дифракційної решітки є її роздільна здатність та кутова дисперсія.

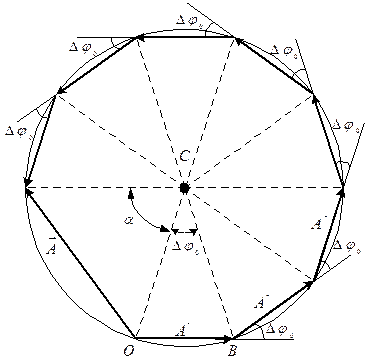
Рис. 5

Роздільна здатність дифракційної решітки визначається за формулою

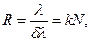(16)

де δλ - різниця довжин хвиль, дифракційні максимуми яких можна спостерігати роздільно;

N - загальна кількість штрихів решітки.

Кутова дисперсія решітки визначається за формулою

. (17)

Порядок виконання роботи

1. Ознайомитись з технічним паспортом гоніометра Г5.

2. Перед щілиною коліматора встановити джерело світла.

3. Установити зорову трубу гоніометра так, щоб чітко було видно щілину коліматора.

4. Помістити в середині столика гоніометра дифракційну решітку перпендикулярно до осі коліматора.

5. Між джерелом світла і коліматором встановити жовтий світлофільтр. Установити, по-перше, чітке зображення щілини справа від нульового максимуму, а потім – зліва. Відмітити ці положення за допомогою шкали мікроскопа. Різниця цих відліків дає кут 2φ.

6. Аналогічні вимірювання виконати при встановленні зорової труби на максимуми 2-го, 3-го і т.д. порядків.

7. Замінити жовтий світлофільтр синім, а потім зеленим і повторити п.п.5...6.

8. Результати вимірювань занести в таблицю: