Массы атомов легких изотопов
Основные понятия и формулы
Скорость света в среде
,
где с — скорость света в вакууме; п — показатель преломления среды.
Релятивистская масса
,
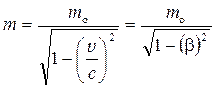где mo — масса покоя частицы; v — ее скорость; с —-скорость света в вакууме; b— скорость частицы, выраженная в долях скорости света (b= v/с).
Взаимосвязь массы и энергии релятивистской частицы
,
где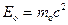 
—энергия покоя частицы.
Полная энергия свободной частицы
,
где Т — кинетическая энергия релятивистской частицы.
Кинетическая энергия релятивистской частицы
.
Импульс релятивистской частицы
.
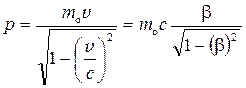Связь между полной энергией и импульсом релятивистской частицы
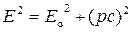
Закон Стефана—Больцмана
,
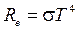где Re — энергетическая светимость абсолютно черного тела, s —постоянная Стефана— Больцмана; Т — термодинамическая температура Кельвина.
Если тело не является абсолютно черным, то закон Стефана—Больцмана применяют в виде
,
где a— коэффициент (степень) черноты тела (a<1).
Закон смещения Вина
,
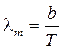где lm — длина волны, на которую приходится максимум энергии излучения; b — постоянная Вина.
Максимальная спектральная плотность энергетической светимости абсолютно черного тела
,
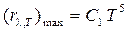где С1 = 1,29 10-5 Вт/(м3 К5).
Энергия фотона
,
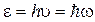где h — постоянная Планка;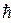 
— постоянная Планка, деленная на 2p; n — частота фотона; w — циклическая частота.
Масса фотона
.
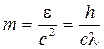где с — скорость света в вакууме; l — длина волны фотона.
Импульс фотона
.
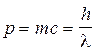Формула Эйнштейна для фотоэффекта
где hn — энергия фотона, падающего на поверхность металла; А — работа выхода электрона; Tmax— максимальная кинетическая энергия фотоэлектрона.
Красная граница фотоэффекта
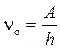, или 
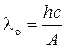
где no — минимальная частота света, при которой еще возможен фотоэффект; lо — максимальная длина волны света, при которой еще возможен фотоэффект; h — постоянная Планка; с — скорость света в вакууме.
Формула Комптона
,
где l1 — длина волны фотона, встретившегося со свободным или слабосвязанным электроном; l2 — длина волны фотона, рассеянного на угол q после столкновения с электроном; то — масса покоящегося электрона.
Комптоновская длина волны
.
Давление света при нормальном падении на поверхность
,
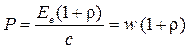где Ее — энергетическая освещенность, w — объемная плотность энергии излучения; r — коэффициент отражения.
Момент импульса электрона согласно теории Бора для атома водорода
,
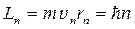где m — масса электрона; vn — скорость электрона на n-й орбите; rn — радиус n-й стационарной орбиты; ћ=h/2p — постоянная Планка; п — главное квантовое число (n= 1, 2,3,...).
Радиус n -й стационарной орбиты
,
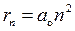где ao — первый боровский радиус.
Энергия электрона в атоме водорода
,
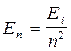где Ei — энергия ионизации атома водорода.
Энергия, излучаемая или поглощаемая атомом водорода,
,
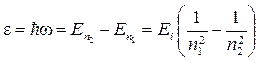где п1 и п2 — квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.
Спектроскопическое волновое число
,
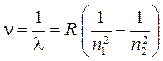где l — длина волны излучения или поглощения атомом; R — постоянная Ридберга.
Длина волны де Бройля
,
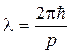где р — импульс частицы.
Импульс частицы и его связь с кинетической энергией Т:
a) 
при v <<c (нерелятивистский случай),
б)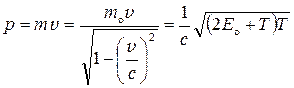 
при v£c (релятивистский случай),
где то — масса покоя частицы; т — релятивистская масса; v — скорость частицы; с — скорость света в вакууме; Еo — энергия покоя частицы (Еo = тоc2)
Соотношение неопределенностей:
а)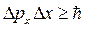 
(для координаты и импульса),
где Dрx, — неопределенность проекции импульса на ось X,Dх — неопределенность координаты;
б)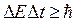 
(для энергии и времени),
где DE — неопределенность энергии; Dt — время жизни квантовой системы в данном энергетическом состоянии.
Одномерное уравнение Шредингера для стационарных состояний
,
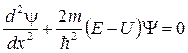где y= y(х) — волновая функция, описывающая состояние частицы; т — масса частицы; Е — полная энергия; U= U(x) — потенциальная энергия частицы.
Плотность вероятности
,
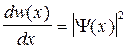где dw(x) — вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dx.
Вероятность обнаружения частицы в интервале от х1 до х2
.
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
а) 
(собственная нормированнаяволновая функция);
б)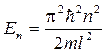 
(собственное значение энергии),
где п—квантовое число (п= 1, 2, 3, ...); l—ширина ящика. В области 0 <x< l U=¥ и y(х)=0.
Массовое число ядра (число нуклонов в ядре)
,
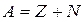где Z — зарядовое число (число протонов); N — число нейтронов.
Закон радиоактивного распада
, или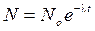 
,
где dN — число ядер, распадающихся за интервал времени dt, N — число ядер, не распавшихся к моменту времени t; No — число ядер в начальный момент (to=0); l— постоянная радиоактивного распада.
Число ядер, распавшихся за время t,
.
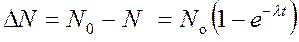В случае, если интервал времени Dt, за который определяется число распавшихся ядер, много меньше периода полураспада T1/2, то число распавшихся ядер можно определить по формуле
.
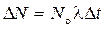Зависимость периода полураспада от постоянной радиоактивного распада
.
Среднее время t жизни радиоактивного ядра, т. е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,
.
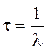Число атомов N, содержащихся радиоактивном изотопе,
,
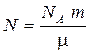где m—масса изотопа; m—молярная масса; Na— постоянная Авогадро.
Активность А радиоактивного изотопа
,
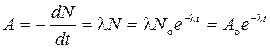где dN — число ядер, распадающихся за интервал времени dt; Ao — активность изотопа в начальный момент времени.
Удельная активность изотопа
.
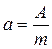Дефект массы ядра,
,
где Z — зарядовое число (число протонов в ядре); А — массовое число (число нуклонов в ядре); (А—Z) — число нейтронов в ядре; mp — масса протона; mn — масса нейтрона; mядр — масса ядра.
Изменение энергии при ядерной реакции определяется соотношением
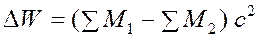
где åM1—сумма масс частиц до реакции и åM2—сумма масс частиц после реакции. Если åM1 > åM2, то реакция идет с выделением энергии, если же åM1 < åM2, то реакция идет с поглощением энергии. Отметим, что в последнюю формулу так же, как и при вычислении энергии связи ядра, мы можем подставлять массу изотопов, а не ядер, так как поправки на массу электронов оболочки входят с разными знаками и поэтому исключаются.
Энергия связи ядра
,
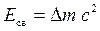где Dm — дефект массы ядра; с — скорость света в вакууме. Во внесистемных единицах энергия связи ядра равна Eсв= 931 Dm, где дефект массы Dm—в а.е.м.; 931— коэффициент пропорциональности (1 а.е.м.~931 МэВ).
Контрольные задачи
1.Частица движется со скоростью v=с/3, где c— скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы?
2.При какой скорости b (в долях скорости света) релятивистская масса любой частицы вещества в п=3 paза больше массы покоя?
3.Определить отношение релятивистского импульса электрона с кинетической энергией T=1,53 МэВ к комптоновскому импульсу moc электрона.
4.Скорость электрона v=0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в единицах МэВ, определить в тех же единицах кинетическую энергию Т электрона.
5.Протон имеет импульс р=469 МэВ/с. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое? (1 МэВ/с=5,33х10-22 кг м/с)
6.Во сколько раз релятивистская масса m электрона, обладающего кинетической энергией Т=1,53 МэВ, больше массы покоя mo?
7.Какую скорость b (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя?
8.При какой скорости v релятивистская масса частицы в k=3 раза больше массы покоя этой частицы?
9.Релятивистский электрон имел импульс р1=тoc. Определить конечный импульс этого электрона (в единицах тoc), если его энергия увеличилась в n=2 раза.
10.Определить скорость v электрона, имеющего кинетическую энергию Т=1,53 МэВ.
11.Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в п=2 раза.
12.Электрон движется, со скоростью v=0,6 с, где с — скорость света в вакууме. Определить релятивистский импульс р электрона.
13.Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный пирометр показывает температуру Tрад=2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна a=0,35.
14.Вычислить энергию, излучаемую за время t=1 мин с площади S=l см2 абсолютно черного тела, температура которого T=1000 К.
15.Черное тело имеет температуру Т1=500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в п=5 раз?
16.Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, lm=0,6 мкм. Определить температуру Т тела.
17.Температура абсолютно черного тела Т=2 кК. Определить длину волны lm, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (rl,T)maxдля этой длины волны.
18.Определить максимальную спектральную плотность (rl,T)max энергетической светимости, рассчитанную на 1 нм в спектре излучения абсолютно черного тела. Температура тела Т=1 К.
19.Определить температуру Т и энергетическую светимость Re абсолютно черного тела, если максимум энергии излучения приходится на длину волны lm=600 нм.
20.Из смотрового окошечка печи излучается поток Фе=4 кДж/мин. Определить температуру Т печи, если площадь окошечка S=8 см2.
21.Поток излучения абсолютно черного тела Фе=10 кВт. Максимум энергии излучения приходится на длину волны lm=0,8 мкм. Определить площадь S излучающей поверхности.
22.Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (lm1=780 нм) на фиолетовую (lm2=390 нм)?
23.Определить поглощательную способность а серого тела, для которого температура, измеренная радиационным пирометром, Tрад=1,4 кК, тогда как истинная температура Т тела равна 3,2 кК.
24.Муфельная печь, потребляющая мощность Р=1 кВт, имеет отверстие площадью S=100 см2. Определить долю h мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК.
25.Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2 мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты а=0,25?
26.Определить энергию e, массу m и импульс р фотона с длиной волны l=1,24 нм.
27.Красная граница фотоэффекта для цинка lo=310 нм. Определить максимальную кинетическую энергию Tmax фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны l=200 нм.
28.На поверхность калия падает свет с длиной волны l=150 нм. Определить максимальную кинетическую энергию Tmax фотоэлектронов.
29.Фотон с энергией e=10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
30.На фотоэлемент с катодом из лития падает свет длиной волны l=200 нм. Найти наименьшее значение задерживающей разности потенциалов Umin, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
31.На пластину падает монохроматический свет (l=0,42 мкм). Фототок прекращается при задерживающей разности потенциалов U=0,95 В. Определить работу А выхода электронов с поверхности пластины.
32.Какова должна быть длина волны излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была vmax=3 Мм/с?
33.На цинковую пластину падает пучок ультрафиолетового излучения (l=0,2 мкм). Определить максимальную кинетическую энергию Tmax и максимальную скорость vmax фотоэлектронов.
34.На металлическую пластину направлен пучок ультрафиолетового излучения (l=0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов Umin=0,96 В. Определить работу выхода А электронов из металла.
35.Определить максимальную скорость vmax фотоэлектрона, вырванного с поверхности металла g-квантом с энергией e=1,53 МэВ.
36.На поверхность металла падает монохроматический свет с длиной волны l=0,1 мкм. Красная граница фотоэффекта lo=0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
37.На металл падает рентгеновское излучение с длиной волны l=1 нм. Пренебрегая работой выхода, определить максимальную скорость vmax фотоэлектронов.
38.На металлическую пластину направлен монохроматический пучок света с частотой n=7,3 1014 Гц. Красная граница lo фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость vmaxфотоэлектронов.
39.На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U=1,5 В. Определить длину волны l света, падающего на пластину.
40.Определить угол q рассеяния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии Dl=3,63 пм.
41.Фотон при эффекте Комптона на свободном электроне был рассеян на угол q=p/2. Определить Импульс р (в МэВ/с), приобретенный электроном, если энергия фотона до рассеяния была e1=1,02 МэВ (1 МэВ/с=5,33х10-22 кг м/с).
42.Рентгеновское излучение (l=1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны lmaxрентгеновского излучения в рассеянном пучке.
43.Фотон с энергией e1, равной энергии покоя электрона (тос2), рассеялся на свободном электроне на угол q=120°. Определить энергию e2 рассеянного фотона и кинетическую энергию Т электрона отдачи (в единицах тос2).
44.Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол q=p/2? Энергия фотона до рассеяния e1=0,51 МэВ.
45.Определить максимальное изменение длины волны (Dl)max, при комптоновском рассеянии света на свободных электронах и свободных протонах.
46.Фотон с длиной волны l1=15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона l2=16 пм. Определить угол q рассеяния.
47.Фотон с энергией e1=0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол q=180°. Определить кинетическую энергию T электрона отдачи.
48.В результате эффекта Комптона фотон с энергией e1=1,02 МэВ рассеян на свободных электронах на угол q=150°. Определить энергию e1 рассеянного фотона.
49.Определить угол q, на который был рассеян квант с энергией e1=1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи T =0,51 МэВ.
50.Фотон с энергией e1=0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния q.
51.Определить импульс ре электрона отдачи, если фотон с энергией e1=1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии.
52.Определить энергетическую освещенность Ее зеркальной поверхности, если давление р,производимое излучением, равно 40 мкПа. Излучение падает нормально к поверхности.
53.Поток энергии, излучаемой электрической лампой, Фе=600 Вт. На расстоянии r=1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром d=2 см. Определить силу F светового давления на зеркальце. Лампу рассматривать как точечный изотропный излучатель.
54.Давление р света с длиной волны l=40 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности.
55.Параллельный пучок монохроматического света с длиной волны l=0,663 мкм падает на зачерненную поверхность и производит на нее давление р=0,3 мкПа. Определить концентрацию п фотонов в световом пучке.
56.Определить коэффициент отражения r поверхности, если при энергетической освещенности Ее=120 Вт/м2 давление р света на нее оказалось равным 0,5 мкПа.
57.Давление света, производимое на зеркальную поверхность, р=5 мПа. Определить концентрацию noфотонов вблизи поверхности, если длина волны света, падающего на поверхность, l=0,5 мкм.
58.На расстоянии r=5 м от точечного монохроматического (l=0,5 мкм) изотропного источника расположена площадка (S=8 мм2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р=100 Вт.
59.На зеркальную поверхность под углом a=60° к нормали падает пучок монохроматического света (l=590 нм). Плотность потока энергии светового потока Ф=1 кВт/м2. Определить давление р, производимое светом на зеркальную поверхность.
60.Свет падает нормально на зеркальную поверхность, находящуюся на расстоянии r=10 см от точечного изотропного излучателя. При какой мощности Р излучателя давление р на зеркальную поверхность будет равным 1 мПа?
61.Свет с длиной волны l=600 нм нормально падает на зеркальную поверхность и производит на нее давление р=4 мкПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности.
62.На зеркальную поверхность площадью S=6 см2падает нормально поток излучения Фе=0,8 Вт. Определить давление р и силу давления F света на эту поверхность.
63.Точечный источник монохроматического (l=1 нм) излучения находится в центре сферической зачерненной колбы радиусом R=10 см. Определить световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р=1 кВт.
64.Невозбужденный атом водорода поглощает квант излучения с длиной волны l=102,6 нм. Вычислить, пользуясь теорией Бора, радиус r электронной орбиты возбужденного атома водорода.
65.Определить энергию e фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной уровень.
66.Вычислить по теории Бора радиус r2 второй стационарной орбиты и скорость v2 электрона на этой орбите для атома водорода.
67.Вычислить по теории Бора период Т вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом п=2.
68.Определить изменение энергии DE электрона в атоме водорода при излучении атомом фотона с частотой n=6,28 1014 Гц.
69.Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны l=97,5 нм?
70.На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны l=435 нм?
71.В каких пределах Dl должна лежать длина волн монохроматического света, чтобы при возбуждении атомов водорода квантами этого света радиус r орбиты электрона увеличился в 16 раз?
72.В однозарядном ионе лития электрон перешел с четвертого энергетического уровня на второй. Определить длину волны l излучения, испущенного ионом лития.
73.Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую Т, потенциальную П и полную Е энергию электрона. Ответ выразить в электрон-вольтах.
74.Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией E=10 эВ. Определить энергию e фотона.
75.Вычислить длину волны де Бройля l для электрона, прошедшего ускоряющую разность потенциалов U=22,5 B.
76.Вычислить длину волны де Бройля l для протона, движущегося со скоростью v=0,6 с (с— скорость света в вакууме).
77.Вычислить наиболее вероятную длину волны де Бройля l молекул азота, содержащихся в воздухе при комнатной температуре.
78.Определить энергию DT, которую необходимо дополнительно сообщить электрону, чтобы его длина волны де Бройля уменьшилась от l1=0,2 мм до l2=0,1 нм.
79.На сколько по отношению к комнатной должна измениться температура идеального газа, чтобы длина волны де Бройля l его молекул уменьшилась на 20%?
80.Параллельный пучок моноэнергетических электронов падает нормально на диафрагму в виде узкой прямоугольной щели, ширина которой а=0,06 мм. Определить скорость этих электронов, если известно, что на экране, отстоящем от щели на расстоянии l=40 мм, ширина центрального дифракционного максимума b=10 мкм.
81.При каких значениях кинетической энергии Т электрона ошибка в определении длины волны де Бройля l по нерелятивистской формуле не превышает 10%?
82.Из катодной трубки на диафрагму с узкой прямоугольной щелью нормально к плоскости диафрагмы направлен поток моноэнергетических электронов. Определить анодное напряжение трубки, если известно, что на экране, отстоящем от щели на расстоянии l=0,5 м, ширина центрального дифракционного максимума Dx=10,0 мкм. Ширину b щели принять равной 0,10 мм.
83.Протон обладает кинетической энергией Т=1 кэВ. Определить дополнительную энергию DT, которую необходимо ему сообщить для того, чтобы длина волны l де Бройля уменьшилась в три раза.
84.Определить длины волн де Бройля a- частицы и протона, прошедших одинаковую ускоряющую разность потенциалов U=1 кВ.
85.Электрон обладает кинетической энергией Т=1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия Т электрона уменьшится вдвое?
86.Кинетическая энергия Т электрона равна удвоенному значению его энергии покоя (2moc2). Вычислить длину волны l де Бройля для такого электрона.
87.Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R=0,05 нм.
88.Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию Tmin электрона, движущегося внутри сферической области диаметром d=0,1 нм.
89.Определить относительную неопределенность Dр/р импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля.
90.Используя соотношение неопределенностей, оценить наименьшие ошибки Dv в определении скорости электрона и протона, если координаты центра масс этих частиц могут быть установлены с неопределенностью 1 мкм.
91.Какова должна быть кинетическая энергия Т протона в моноэнергетическом пучке, используемого для исследования структуры с линейными размерами l » 10-13 см?
92.Используя соотношение неопределенностей, оценить ширину 1 одномерного потенциального ящика, в котором минимальная энергия электрона Emin=10 эВ.
93.Альфа-частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если известно, что минимальная энергия a-частицы Emin=8 МэВ.
94.Среднее время жизни атома в возбужденном состоянии составляет Dt=10-8 с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны <l> которого равна 600 нм. Оценить ширину излучаемой спектральной линии Dl, если не происходит ее уширения за счет других процессов.
95.Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность Dr радиуса r электронной орбиты и неопределенность Dp импульса p электрона на такой орбите соответственно связаны следующим образом: Dr»r и Dp»p. Используя эти соотношения и соотношение неопределенностей, найти значение радиуса электронной орбиты, соответствующего минимальной энергии электрона в атоме водорода.
96.Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно радиусом r»10 см. Пользуясь соотношением неопределенностей, найти, во сколько раз неопределенность Dx координаты электрона на экране в направлении, перпендикулярном оси трубки, меньше размера r пятна. Длину L электронно-лучевой трубки принять равной 0,50 м, а ускоряющее электрон напряжение U — равным 20 кВ.
97.Среднее время жизни Dt атома в возбужденном состоянии составляет около 10-8 с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны <l> которого равна 400 нм. Оценить относительную ширину Dl./l, излучаемой спектральной линии, если не происходит уширения линии за счет других процессов.
98.Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность Dr радиуса r электронной орбиты и неопределенность Dp импульса р электрона на такой орбите соответственно связаны следующим образом: Dr»r и Dp»p. Используя эти связи, а также соотношение неопределенностей, определить минимальное значение энергии Tmin электрона в атоме водорода.
99.Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Найти отношение разности DEn,n+1 соседних энергетических уровней к энергии En частицы в трех случаях: 1) n=2; n=5; 3) n ®¥.
100.Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l=0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.
101.Электрон находится в прямоугольном потенциальном ящике с непроницаемыми стенками. Ширина ящика l=0,2 нм, энергия электрона в ящике Е=37,8 эВ. Определить номер п энергетического уровня и модуль волнового вектора (k=2p/l).
102.Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы: в средней трети ящика? в крайней трети ящика?
103.Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l находится в возбужденном состоянии (n=3). Определить, в каких точках интервала 0<х<l плотность вероятности нахождения частицы имеет максимальное и минимальное значения.
104.В прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками (0<х<.l) находится частица в основном состоянии. Найти вероятность w местонахождения этой частицы в области 1/4l<х <3/4l.
105.Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность w обнаружения частицы в крайней четверти ящика?
106.Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид y(r)=A exp(-r/ao), где А — некоторая постоянная; аo — первый боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.
107.Частица находится в основном состоянии в прямоугольной яме шириной l с абсолютно непроницаемыми стенками. Во сколько раз отличаются вероятности местонахождения частицы: w1 — в крайней трети и w2 — в крайней четверти ящика?
108.Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид y(r)=A exp(-r/ao), где А — некоторая постоянная; аo— первый боровский радиус. Найти для основного состояния атома водорода среднее значение <F> кулоновской силы.
109.Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале 0<х<l плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.
110.Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид y(r)=A exp(-r/ao), где А — некоторая постоянная; аo — первый боровский радиус. Найти для основного состояния атома водорода среднее значение <П> потенциальной энергии.
111.Найти период полураспада T1/2 радиоактивного изотопа, если его активность за время t=10 сут уменьшилась на 24% по сравнению с первоначальной.
112.Определить, какая доля радиоактивного изотопа 89Ac225 распадается в течение времени t=6 сут.
113.Активность А некоторого изотопа за время t=10 сут уменьшилась на 20%. Определить период полураспада T1/2 этого изотопа.
114.Определить массу m изотопа 53I131, имеющего активность А=37 ГБк.
115.Найти среднюю продолжительность жизни t атома радиоактивного изотопа кобальта 27Co60.
116.Счетчик a-частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал N1=1400 частиц в минуту, а через время t=4 ч — только N2=400. Определить период полураспада T1/2 изотопа.
117.Во сколько раз уменьшится активность изотопа 15P32 через время t=20 сут?
118.На сколько процентов уменьшится активность изотопа иридия 77Ir192 за время t=15 сут?
119.Определить число N ядер, распадающихся в течение времени: 1) t1=1 мин; 2) t2=5 сут, — в радиоактивном изотопе фосфора 15P32 массой m=1 мг.
120.Изотопы какого элемента образуются из 
случае: 1) b–-распада;
2) К-захвата? Сколько протонов и нейтронов они содержат?
121.Вычислить энергию связи Есв ядра дейтерия 1H2 и трития 1H3.
122.Определить число N атомов радиоактивного препарата йода 53I131 массой т=0,5 мкг, распавшихся в течение времени: 1) t1=1 мин; 2) t2=7 суток.
123.Определить активность А радиоактивного препарата массой т=0,1 мкг.
124.Период полураспада радия 1600 лет. Через какое время число атомов уменьшится в 4 раза?
125.Чему равна активность радона, образовавшегося из 1 г радия за один час? (Период полураспада радона 3,8 дня)
126.К 10 мг радиоактивного изотопа 20Са45 примешано 30 мг нерадиоактивного изотопа 20Са40. Насколько уменьшилась удельная активность препарата?
127.Грибы, собранные в лесу имели по цезию-137 активность, равную 68500 Бк на 1 кг сухой биомассы. По истечении какого времени удельная активность этих грибов снизится до 3700 Бк/кг?
128.Найти число протонов и нейтронов, входящих в состав ядер трех изотопов магния: 1) 12Mg24, 2) 12Mg25 и 3) 12Mg26.
129.Найти энергию связи ядра изотопа лития 3Li7.
130.Найти энергию, освобождающуюся при ядерной реакции
3Li7 +1H1 ® 2He4 +2He4.
ТАБЛИЦЫ ВАРИАНТОВ КОНТРОЛЬНЫХ РАБОТ
| Вариант | Номера задач | ||||||||||
ПРИЛОЖЕНИЯ
1. Основные физические постоянные (округленные значения), используемые в разделе 1
| Элементарный заряд | е | 1,60×10-19 Кл |
| Скорость света в вакууме | с | 3,00×108 м/с |
| Постоянная Стефана—Больцмана | s | 5,67×10-8 Вт/ (м2 К4) |
| Постоянная закона смещения Вина | b | 2,90×10-3 м К |
| Постоянная Планка | h | 6,63×10-34 Дж с |
| Постоянная Планка | ћ=h/2p | 1,05×10-34 Дж с |
| Постоянная Ридберга | R | 1,10×10-7 м-1 |
| Радиус Бора | ao | 0,529×10-10 м |
| Комптоновская длина волны электрона | L | 2,43×10-12 м |
| Энергия ионизации атома водорода | Еi | 2,18×10-18 Дж (13,6 эВ) |
| Атомная единица массы | а.е.м. | 1,660×10-27 кг |
| Электрическая постоянная | eо | 8,85×10-12 Ф/м |
| Магнитная постоянная | mо | 4p×10-7 Гн/м |
Энергия ионизации
| Вещество | Еi, Дж | Еi, эВ |
| Водород Гелий Литий Ртуть | 2,18×10-18 3,94×10-18 1,21×10-18 1,66×10-18 | 13,6 24,6 75,6 10,4 |
Показатель преломления
| Вещество | Показатель |
| Алмаз Вода Глицерин Стекло | 2,42 1,33 1,47 1,50 |
Работа выхода электронов
| Металл | А, Дж | А, эВ | Металл | А, Дж | А, эВ | |||||||
| Калий Литий Платина Рубидий | 3,5 ×10-19 3,7 ×10-19 10× 10-19 3,4 ×10-19 | 2,2 2,3 6,3 2,1 | Серебро Цезий Цинк | 7,5 ×10-19 3,2× 10-19 6,4 ×10-19 | 4,7 2,0 4,0 | |||||||
Массы атомов легких изотопов