Идеал сұйықтықтағы гидродинамикалық қысым
Дәріс. Идеал сұйықтықтар динамикасының негізгі теңдеулері. Сұйықтық пен газ физикасы есептерінің жалпы қойылымы. Сығылмайтын және сығылатын сұйықтық жағдайлары. Баротроптық және бароклиндік. Энергия құйылу теңдеуі.
Массалық және беттік күштері.Сұйықтықта, 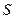 тұйық бетпен шектелген кейбір
тұйық бетпен шектелген кейбір 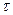 көлемін бөліп аламыз (4.1 сур.). Сұйықтықтың бөлінген көлеміне әсер ететін күштерді екі класқа бөлуге болады.
көлемін бөліп аламыз (4.1 сур.). Сұйықтықтың бөлінген көлеміне әсер ететін күштерді екі класқа бөлуге болады.
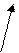
 z n
z n

 s
s 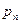
 |
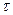

 0 y
0 y
x
4.1 сур. Сұйықтықтың бөлінген көлеміне беттік күштердің әcер ету сұлбасы.
Бірінші класқа біздер 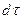 көлемнің әр элементіне әсер ететін,
көлемнің әр элементіне әсер ететін, 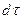 көлемнің қасында сұйықтықтың басқа бөлшектері бар немесе жоқ болатынына тәуелсіз күштерді жатқызамыз. Бұл күштерді біздер массалық немесе көлемдік деп атаймыз. Егер
көлемнің қасында сұйықтықтың басқа бөлшектері бар немесе жоқ болатынына тәуелсіз күштерді жатқызамыз. Бұл күштерді біздер массалық немесе көлемдік деп атаймыз. Егер 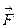 арқылы, массаның бірлігіне қатынасты, массалық күштердің векторын атасақ, онда тығыздығы
арқылы, массаның бірлігіне қатынасты, массалық күштердің векторын атасақ, онда тығыздығы 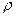 сұйықтықтың
сұйықтықтың 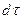 көлем элементіне
көлем элементіне 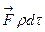 массалық күші әсер етеді; бүкіл
массалық күші әсер етеді; бүкіл 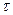 көлемге әсер ететін массалық күштердің бас векторы,
көлемге әсер ететін массалық күштердің бас векторы, 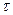 көлемі бойынша таратылған векторлық интегралымен
көлемі бойынша таратылған векторлық интегралымен 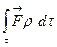 өрнектеледі, ал бас вектордың Оx, Oy, Oz декарт координаталар осьтеріне проекциялары сәйкес болады:
өрнектеледі, ал бас вектордың Оx, Oy, Oz декарт координаталар осьтеріне проекциялары сәйкес болады:
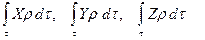 ,
,
мұнда 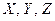 -
- 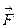 вектордың проекциялары.
вектордың проекциялары.
Координаталар басына қатысты, 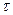 көлеміне әсер ететін (түсірілген) массалық күштерінің бас моменті векторлық интегралымен
көлеміне әсер ететін (түсірілген) массалық күштерінің бас моменті векторлық интегралымен 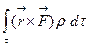 өрнектеледі, мұнда
өрнектеледі, мұнда 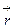 -
- 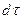 бөлшектің радиус-векторы; бас моментің Оx, Oy, Oz декарт координаталар осьтеріне проекциялары келесі интералдарға сәйкес болады:
бөлшектің радиус-векторы; бас моментің Оx, Oy, Oz декарт координаталар осьтеріне проекциялары келесі интералдарға сәйкес болады:
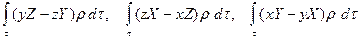

Ауырлық күші, инерция күші және басқалары массалық күшінің мысалдары болып табылады.
Екінші күштер класына қарастырып жатқан 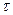 көлеміне әсер ететін, біздер сұйықтықтың әр түрлі бөлшектерінің арасындағы бір – бірімен әсер ететін күштерді жатқызамыз. Әрекет және қарсы әрекет теңдік принципі бойынша
көлеміне әсер ететін, біздер сұйықтықтың әр түрлі бөлшектерінің арасындағы бір – бірімен әсер ететін күштерді жатқызамыз. Әрекет және қарсы әрекет теңдік принципі бойынша 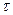 көлемінің барлық ішкі бөлшектерінің арасындағы бір – бірімен әсер ету күштері тепе –теңдікке келеді, тек
көлемінің барлық ішкі бөлшектерінің арасындағы бір – бірімен әсер ету күштері тепе –теңдікке келеді, тек 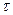 көлемнің беттік бөлшектеріне әсер ететін күштер,
көлемнің беттік бөлшектеріне әсер ететін күштер, 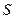 беттің сыртында жатқан бөлшектерден пайда болатын, тепе –теңсіздікте болуы мүмкін. Осындай күштерді беттік деп атайды. Егер
беттің сыртында жатқан бөлшектерден пайда болатын, тепе –теңсіздікте болуы мүмкін. Осындай күштерді беттік деп атайды. Егер 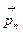 арқылы аудан бірлігіне қатынасты, беттік күш векторын белгілесек, онда
арқылы аудан бірлігіне қатынасты, беттік күш векторын белгілесек, онда 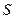 беттің
беттің 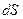 элементар ауданында
элементар ауданында 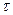 көлемге, сыртқы бөлшектерден пайда болатын
көлемге, сыртқы бөлшектерден пайда болатын 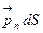 күші әсер етеді;
күші әсер етеді; 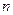 таңбасы
таңбасы 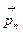 векторы
векторы 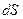 элементар ауданның бағыттауынан (бағдарлауынан) тәуелді екендігін көрсетеді, яғни сыртқы нормаль бағытынан.
элементар ауданның бағыттауынан (бағдарлауынан) тәуелді екендігін көрсетеді, яғни сыртқы нормаль бағытынан.
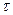 көлемге әсер ететін, беттік күштердің бас векторы және бас моменті, бүкіл
көлемге әсер ететін, беттік күштердің бас векторы және бас моменті, бүкіл 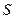 тұйық бет бойынша таратылған интегралдарымен өрнектеледі:
тұйық бет бойынша таратылған интегралдарымен өрнектеледі:
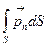 және
және 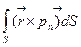 .
.
Қозғалыстың жалпы теңдеуі. Кез келген материалды жүйенің әр қозғалыс сәтінде осыған әсер ететін барлық күштер, инерция күшін және қосканда, бір – бірімен тепе – теңдікте болады деп айтылатын Даламбер принципін қолданайық, сонда
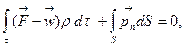 (4.1)
(4.1)
мұнда 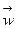 -
- 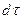 элементтің үдеуі; сонда
элементтің үдеуі; сонда 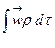 - инерция күшінің бас векторын өрнектейді.
- инерция күшінің бас векторын өрнектейді.
Идеал сұйықтықтағы гидродинамикалық қысым
Идеал сұйықтықта үйкеліс күштері байқалмайды, және кішкене нормаль созылу сұйықтық тұтастығының үзілуіне әкеледі; демек идеал сұйықтықтың 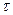 көлемінің
көлемінің 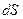 бет элементтеріне әсер ететін беттік күштері, көлем ішіне бағытталған нормаль кысымдар болып табылады; басқаша айтқанда
бет элементтеріне әсер ететін беттік күштері, көлем ішіне бағытталған нормаль кысымдар болып табылады; басқаша айтқанда 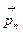 векторы
векторы 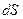 элементке ішкі нормаль бойымен бағытталған. Идеал сұйықтық үшін осы
элементке ішкі нормаль бойымен бағытталған. Идеал сұйықтық үшін осы 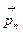 вектор шамасы
вектор шамасы 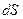 ауданның бағыттауынан тәуелсіз екендігін көрсетеміз. Ол үшін сұйықтықта КАВС (4.2 сур.) элементар тетраэдраның көлемін қарастырайық, оның үш жағы КВС, КАС және КАВ координаталар жазықтықтарына параллель, демек сыртқы нормальдары осы жақтарға Ох, Оy және Оz остеріне сәйкес кері бағытталған; одан әрі
ауданның бағыттауынан тәуелсіз екендігін көрсетеміз. Ол үшін сұйықтықта КАВС (4.2 сур.) элементар тетраэдраның көлемін қарастырайық, оның үш жағы КВС, КАС және КАВ координаталар жазықтықтарына параллель, демек сыртқы нормальдары осы жақтарға Ох, Оy және Оz остеріне сәйкес кері бағытталған; одан әрі 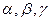 арқылы төртінші АВС көлбеу жағына
арқылы төртінші АВС көлбеу жағына 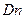 сыртқы нормальдің координаталар остерімен пайда болған бұрыштардың косинустерін белгілейік; енді соңында АВС жақтың ауданы
сыртқы нормальдің координаталар остерімен пайда болған бұрыштардың косинустерін белгілейік; енді соңында АВС жақтың ауданы 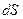 -ке тең болсын, сонда КВС, КАС, КАВ жақтардың аудандары,
-ке тең болсын, сонда КВС, КАС, КАВ жақтардың аудандары, 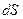 ауданның проекциялары болып, сәйкес
ауданның проекциялары болып, сәйкес 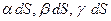 болады.
болады.
(4.1) теңдеуді тетраэдраның 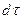 көлеміне пайдалансақ, аламыз:
көлеміне пайдалансақ, аламыз:
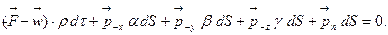 (4.2)
(4.2)







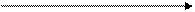

 z
z
 С n
С n
D
К
В
А
y
x
4.2 сур. Тетраэдраның элементар көлеміне беттік күштің әсер ету сұлбасы.
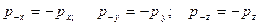 ескереміз және
ескереміз және 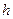 арқылы тетраэдраның KD биіктігін белгілеп, аламыз
арқылы тетраэдраның KD биіктігін белгілеп, аламыз
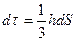 .
.
Сондықтан 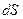 -ке қысқартқаннан кейін (4.2) теңдеуі мына түрге келеді:
-ке қысқартқаннан кейін (4.2) теңдеуі мына түрге келеді:
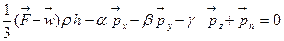 ,
,
бұдан 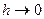 кезінде шекке өтіп, беттік күштердің негізгі қасиетіне келеміз:
кезінде шекке өтіп, беттік күштердің негізгі қасиетіне келеміз:
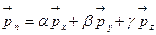 , (4.3)
, (4.3)
Бұл қасиет 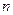 сыртқы нормальдің кез келген бағытта болғандағы
сыртқы нормальдің кез келген бағытта болғандағы 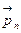 векторын, негізгі
векторын, негізгі 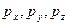 үш векторлары берілгенде анықтауға болатынын көрсетеді.
үш векторлары берілгенде анықтауға болатынын көрсетеді. 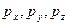 векторлары элементар аудандар үшін, олардың сыртқы нормальдары ОХ, ОY, OZ өстерімен параллель және бірдей бағытталған жағдайдағы беттік күштерді өрнектейді. (4.3) формуласымен өрнектелетін қасиет, элементар ауданның әр түрлі бағыттауда болғандағы алынатын
векторлары элементар аудандар үшін, олардың сыртқы нормальдары ОХ, ОY, OZ өстерімен параллель және бірдей бағытталған жағдайдағы беттік күштерді өрнектейді. (4.3) формуласымен өрнектелетін қасиет, элементар ауданның әр түрлі бағыттауда болғандағы алынатын 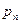 векторлардың жиыны тензор құрайды екенін көрсетеді; ол серпімді кернеулер тензоры деп аталады.
векторлардың жиыны тензор құрайды екенін көрсетеді; ол серпімді кернеулер тензоры деп аталады.
Кез келген сұйықтыққа әділетті (4.3) формуланы идеал сұйықтық жағдайда қолданайық. Бұл жағдайда 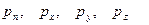 векторлары
векторлары 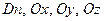 сыртқы нормальдарға кері бағытталған болады және (4.3)-ті Ox, Oy, Oz өстеріне біртіндеп проекциялап, аламыз:
сыртқы нормальдарға кері бағытталған болады және (4.3)-ті Ox, Oy, Oz өстеріне біртіндеп проекциялап, аламыз:
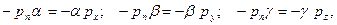
бұдан
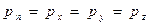 , (4.4)
, (4.4)
яғни идеал сұйықтық үшін нормаль қысым шамасы элементар ауданның, өзі соған әсер ететін, бағдарлауынан (бағыттауынан) тәуелсіз болады. Осыған байланысты бағытты көрсетпей, белгідегі таңбаны алып тастауға болады және гидродинамикалық қысым ауданға ішкі нормаль бойымен бағытталған екенін ұмытпай.
Идеал сұйықтық қозғалысының жалпы теңдеулері. (4.1) теңдеуі идеал сұйықтық жағдайда мына түрге келеді:
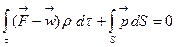 (4.5)
(4.5)
және гидродинамикалық қысым векторы 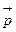
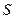 бетке ішкі нормаль бойымен бағытталған. Сыртқы нормальдің
бетке ішкі нормаль бойымен бағытталған. Сыртқы нормальдің 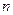 ортын қарастыра отырып, аламыз:
ортын қарастыра отырып, аламыз: 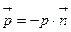 және алдындағы теңдеу мына түрге келеді:
және алдындағы теңдеу мына түрге келеді:
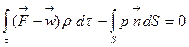 . (4.6)
. (4.6)
Соңғы интегралға Гаусс түрлендіруін пайдаланып, аламыз:
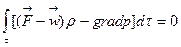 .
.
Қарастырып жатқан 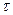 көлемі кез келген болғандықтан, сұйықтың әр нүктесінде және қозғалыстың кез келген сәтінде интеграл ішіндегі өрнек нөлге тең болуы керек. Сондықтан, идеал сұйықтық қозғалысының негізгі теңдеуіне келеміз:
көлемі кез келген болғандықтан, сұйықтың әр нүктесінде және қозғалыстың кез келген сәтінде интеграл ішіндегі өрнек нөлге тең болуы керек. Сондықтан, идеал сұйықтық қозғалысының негізгі теңдеуіне келеміз:
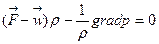 . (4.7)
. (4.7)
немесе проекцияларда:
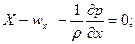
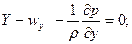 (4.8)
(4.8)
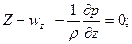
Эйлер түріндегі қозғалыс теңдеулері.Кинематикалық формулалар бойынша Эйлер айнымалыларында үдеу проекцияларын өрнектеп:
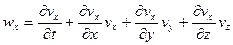 ,
,
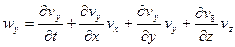 ,
,
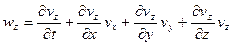 ,
,
және (4.8) теңдеулерді 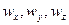 арқылы шешіп, Эйлер гидродинамикалық теңдеулерін аламыз:
арқылы шешіп, Эйлер гидродинамикалық теңдеулерін аламыз:

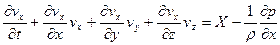 ,
,
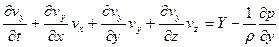 , (4.9)
, (4.9)
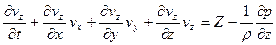 .
.
Сұйықтық пен газ физикасы есептерінің жалпы қойылымы. Сығылмайтын және сығылатын сұйықтық жағдайлары. Баротроптық және бароклиндік. Энергия құйылу теңдеуі.
Материалдық бөлшектердің жиыны ретінде сұйықтықты қарастырайық (кеңістікті немесе оның бөлігін тұтас толтыратын). Бөлшектердің арасында гидродинамикалық күші арқылы идеал сұйықтықты өрнектейтін, бір – бірімен әсер ететін ішкі күштері пайда болады. Сұйықтық пен газ физикасы есептерінің жалпы қойылымын былайша тұжырымдауға болады: берілген сыртқы күштердің әсерінен әр бөлшектің қозғалысын және ішкі күштерді, яғни гидродинамикалық қысымды, сұйықтықтың әр нүктесінде және қозғалыстың әр сәтінде анықтау керек.
Сығылмайтын және сығылатын сұйықтық жағдайларды бөлек қарастырамыз, екі жағдайда да сұйықтықтыны идеал және қарапайым үшін біртекті деп есептейміз.
 Сығылмайтын сұйықтық жағдайы.Сығылмайтын сұйықтықта тығыздық
Сығылмайтын сұйықтық жағдайы.Сығылмайтын сұйықтықта тығыздық 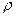 , сұйықтықтың берілген сортына физикалық сипатамасын беретін, тұрақты болады және белгілі деп есептеледі. Эйлер теңдеулерін алып, мұнда төрт белгісіз шамалар бар екенін байқаймыз:
, сұйықтықтың берілген сортына физикалық сипатамасын беретін, тұрақты болады және белгілі деп есептеледі. Эйлер теңдеулерін алып, мұнда төрт белгісіз шамалар бар екенін байқаймыз: 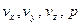 - төрт дифференциалдық теңдеулер жүйесінен:
- төрт дифференциалдық теңдеулер жүйесінен:
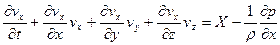 ,
,
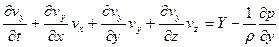 , (4.10)
, (4.10)
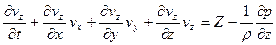 .
.
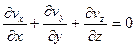 .
.
Егер бұл жүйені интегралдауға мүмкіндік болса, онда әр уақыт сәтінде жылдамдықтың векторлық өрісі және қысымның скаляр өрісі анықталатын болады, яғни (4.10) жүйесін қанағаттандыратын функциялары
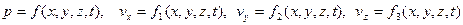 ,
,
табылатын болады. Есепті соңына дейін жеткізу және әр бөлшектің қозғалыс теңдеуін, яғни 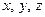 бөлшек координаталарының уақыттан
бөлшек координаталарының уақыттан 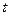 және координаталардың бастапқы мәндерінен
және координаталардың бастапқы мәндерінен 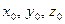 байланысын анықтау үшін тағы үш теңдеу жүйесін
байланысын анықтау үшін тағы үш теңдеу жүйесін
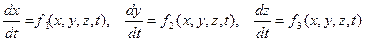 (4.11)
(4.11)
интегралдау қажет.
Сығылатын сұйықтық жағдайы. Баротроптық және бароклиндік. Энергия құйылу теңдеуі.
Енді сығылатын сұйықтық қозғалысын анықтау есебіне көшімез. Математикалық өте қарапайым сол дербес жағдайы болады, қашан барлық қозғалыста тығыздық алдын ала белгілі қысым функциясы болса, яғни
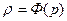 .
.  (4.12)
(4.12)
Тығыздығы тек бір қысымнан тәуелді функция болатын орталарды баротропты деп атайды. Баротроптық сұйықтықтардың үзіксіздік теңдеуі
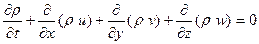
және (4.11)-дің бірінші үш қозғалыс теңдеулері тұйықталады, өйткені осы төрт теңдеулерге қажетті төрт ізделетін функциялары кіреді, себебі белгісіз шамалар ретінде 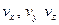 және
және 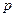 қалдырып, (4.3) пайдалана отырып
қалдырып, (4.3) пайдалана отырып 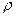 тығыздықты қарастырмауға болады.
тығыздықты қарастырмауға болады.
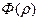 үшін ең қарапайым мысал заңы
үшін ең қарапайым мысал заңы 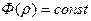 болады. Бұл сығылмайтын сұйықтық жағдайы.
болады. Бұл сығылмайтын сұйықтық жағдайы.
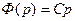 қозғалыстарды изотермиялық қозғалыстар деп атайды, мұнда
қозғалыстарды изотермиялық қозғалыстар деп атайды, мұнда 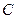 – тұрақты.
– тұрақты.
Егер 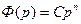 , онда политропты процестер туралы айтады және
, онда политропты процестер туралы айтады және 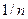 шама политроптың көрсеткіші деп аталады, мұнда
шама политроптың көрсеткіші деп аталады, мұнда 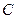 және
және 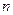 - тұрақтылар. Баротропты сұйықтықтар үшін осындай ең қарапайым және жиі қолданылатын
- тұрақтылар. Баротропты сұйықтықтар үшін осындай ең қарапайым және жиі қолданылатын 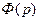 функциялардың түрлері.
функциялардың түрлері.
Тығыздығы тек жалғызғана қысым функциясы болмайтын, яғни оларға ішқандай (4.12) орындалатындай 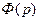 функциясы табылмайтын орталарды бароклинды деп атайды. Мұнда тығыздық
функциясы табылмайтын орталарды бароклинды деп атайды. Мұнда тығыздық 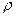 , анықталатын, бесінше белгісіз шама болып табылады және сондықтан біздің төрт теңдеуіміз (үзіксіздік теңдеу және қозғалыстың үш теңдеуі) есепті шығару үшін жеткіліксіз.
, анықталатын, бесінше белгісіз шама болып табылады және сондықтан біздің төрт теңдеуіміз (үзіксіздік теңдеу және қозғалыстың үш теңдеуі) есепті шығару үшін жеткіліксіз.
Жалпы бароклинды сығылатын сұйықтық жағдайда, қозғалысты зерттеу үшін энергия құйылу (келу) деген жаңа факторды ескеру қажет екен. Бұл жағдай екі жаңа шаманы қарастыруға енгізеді: 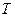 сұйықтықтың температурасы (абсолюттік) және
сұйықтықтың температурасы (абсолюттік) және 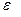 энергия құйылуының жылу қуатының тығыздығы, яғни сұйықтық көлем бірлігінің уақыт бірлігінде алатын энергия мөлшері.
энергия құйылуының жылу қуатының тығыздығы, яғни сұйықтық көлем бірлігінің уақыт бірлігінде алатын энергия мөлшері.
Энергия құйылу теңдеуі мына түрде жазылады:
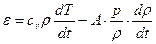 , (4.13)
, (4.13)
мұнда 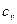 - тұрақты көлемдегі жылусыйымдылық,
- тұрақты көлемдегі жылусыйымдылық, 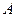 - жұмыстың термиялық эквиваленті (
- жұмыстың термиялық эквиваленті ( 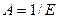 , мұнда
, мұнда 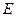 -жылудың механикалық эквиваленті).
-жылудың механикалық эквиваленті).
(4.13) теңдеуден басқа 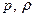 және
және 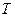 байланыстыратың тағы да бір арақатысты жазуымыз керек. Кемелденген газдар үшін осындай арақатыс Клайперон теңдеуі болады.
байланыстыратың тағы да бір арақатысты жазуымыз керек. Кемелденген газдар үшін осындай арақатыс Клайперон теңдеуі болады.
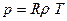 , (4.14)
, (4.14)
мұнда 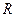 - газ тұрақтысы.
- газ тұрақтысы.
Сонымен бізде алты теңдеулері бар : үзіксіздік теңдеуі, қозғалыстың үш теңдеуі, энергия құйылу теңдеуі және (4.14) күй теңдеуі. Осы теңдеулерге керекті алты 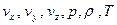 белгісіз шамалар кіреді. Өкініш орай (4.13)-ке кейбір жағдайда белгілі деп есептей алмайтын шама кіреді. Сырттан жылу келу жоғы ең қарапайым және маңызды жағдай болып табылады, яғни
белгісіз шамалар кіреді. Өкініш орай (4.13)-ке кейбір жағдайда белгілі деп есептей алмайтын шама кіреді. Сырттан жылу келу жоғы ең қарапайым және маңызды жағдай болып табылады, яғни
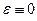 . (4.15)
. (4.15)
Осы жағдайда (4.14) пайдаланып (4.13) мына түрде жазуға болады:
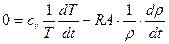 ,
,
содан соң тағы да бір рет (4.14) пайдаланып, 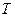 алып тастауға болады. Нәтижесінде аламыз:
алып тастауға болады. Нәтижесінде аламыз:
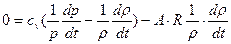 ,
,
немесе 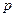 және
және 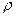 бар мүшелерді жинап, табамыз:
бар мүшелерді жинап, табамыз:
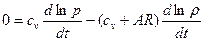 .
.
Термодинамиканың арақатысын еске алып
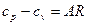 ,
,
мұнда 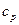 - тұрақты қысымдағы жылусыйымдылық, ақырында
- тұрақты қысымдағы жылусыйымдылық, ақырында 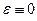 жағдай үшін энергия құйылу теңдеуін мына түрде аламыз
жағдай үшін энергия құйылу теңдеуін мына түрде аламыз
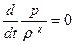 , (4.16)
, (4.16)
мұнда 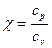 (4.17)
(4.17)
Осындай сұйықтық қозғалысы адиабаттық қозғалыс деп аталады.
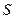 энтропиямен
энтропиямен 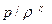 шамасы
шамасы
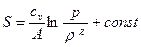 . (4.18)
. (4.18)
қатысымен байланыста.
(4.16) бойынша 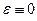 кезінде энтропия бөлшекте сақталады.
кезінде энтропия бөлшекте сақталады.
