ЛАБОРАТОРНАЯ РАБОТА № 3-1М Интерференция света на двух щелях

Цель работы: наблюдение дифракции на одной щели и интерференции от двух щелей, измерение ширины щелей и расстояния между ними.

Оборудование: Оптическая скамья, гелий-неоновый лазер ГН-3, дифракционный объект МОЛ-1, экран, видеокамера, компьютер.

Методика эксперимента.

Рассмотрим дифракцию плоской монохроматической волны от щели. Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины. Обозначим ширину щели 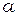(рис. 1).

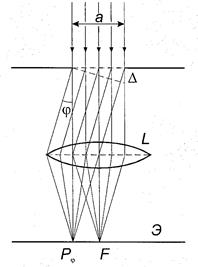
Рис. 1.

Пусть световая волна длиной 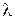падает нормально к плоскости щели. За щелью установлена собирательная линза L, в фокальной плоскости которой находится экран Э. Параллельный пучок лучей, пройдя через щель, дифрагирует (отклоняется) под разными углами вправо и влево от первоначального направления. Линза собирает параллельные пучки дифрагированных лучей под углом 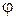в соответствующих точках экрана Э, причём разность хода 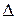между лучами идущих от различных точек волнового фронта внутри щели зависит от угла дифракции 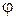и определяется формулой:

.

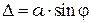Обратим внимание на то, что разность хода между лучами, идущими от краёв щели, зависит от синуса угла дифракции 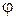. Линза дополнительной разности хода не вносит.

Тип дифракции, при котором рассматривается дифракционная картина, формируемая параллельными лучами, получил название дифракции в параллельных лучах или дифракции Фраунгофера.

Расчёт даёт формулу распределения интенсивности света на экране Э в зависимости от угла дифракции виде:

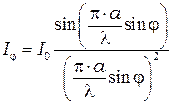, (1)

где 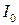- интенсивность света в середине дифракционной картины (в направлении 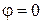); 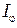- интенсивность света в точке, положение которой определяется данным значением угла 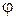. Числитель в (1) обращается в нуль при значении угла дифракции 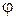, удовлетворяющего условию:

,

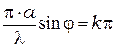где 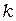= ±1, ±2, ±3…., соответственно, интенсивность света равна нулю при условии

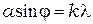. (2)

Эта формула – условие дифракционного минимума. Такая же формула условия минимума получается, если для расчёта амплитуды дифрагированных волн использовать метод полуволновых зон Френеля.

Из формулы (2) следует, что интенсивность на экране равна нулю во всех случаях, когда разность хода между крайними лучами 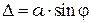равна 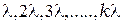, т.е. минимумы освещенности соответствуют направлениям дифрагированных лучей под углом :

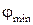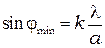, (3)

где 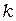- целое число.

Направления, в которых возникают максимумы, определяются формулой:

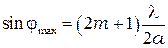. (4)

Распределение интенсивности света в фокальной плоскости L представлено на рис. 2. Центральная светлая полоса - максимум нулевого порядка - занимает область между ближайшими правыми и левыми минимумами, т.е. область

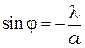и .

И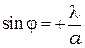нтенсивность света 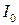максимума нулевого порядка определяется квадратом амплитуды электрического поля 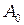падающей волны. Интенсивность максимумов более высокого порядка первого, второго и т.д., значительно уступают по величине центральному максимуму.

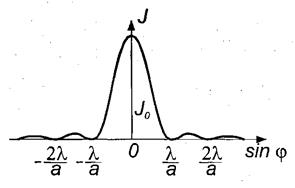
Рис. 2

Расчёты показывают, что интенсивности центрального и следующих максимумов относятся как 1:0,045:0,016 и т.д.

Если используются две узкие щели, освещаемые параллельным пучком излучения лазера (плоской монохроматической волной), то вследствие дифракции пучки излучения после щелей получаются расходящимися, благодаря чему перекрываются и дают интерференционную картину.

Рассмотрим интерференцию от двух параллельных щелей одинаковой ширины 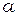и расположенных на расстоянии 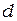друг от друга. Интерференционная картина наблюдается в фокальной плоскости линзы L. (рис.4, а). Пусть на объект с двумя щелями падает плоская монохроматическая волна длиной .

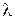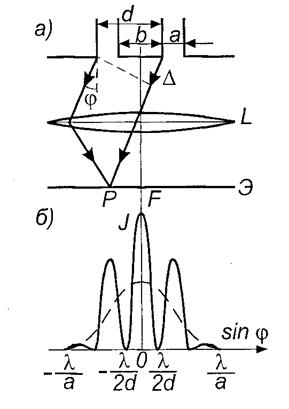
Рис. 3

Перемещение щели параллельно самой себе не приводит к изменению дифракционной картины, это значит, что положение дифракционных максимумов и минимумов от одной щели не зависит от её положения, а определяется только направлением дифрагированных лучей. Поэтому картины, создаваемые каждой щелью в отдельности, будут совершенно одинаковыми.

Результирующую картину можно определить путем сложения этих двух картин с учётом интерференции волн, идущих от каждой из щелей. Очевидно, что в тех направлениях, в которых ни одна из щелей света не даёт света, не будет света и при двух параллельных щелях. Условие дифракционного минимума интенсивности

,

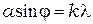где 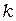= ±1, ±2, ±3, ..., выполняется и в данном случае.

Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, из-за интерференции взаимно уничтожаются. Возникают добавочные интерференционные минимумы. Они будут наблюдаться в тех направлениях, которым соответствует разность хода, удовлетворяющая условию интерференционного минимума

.

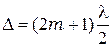Разность хода между параллельными лучами, дифрагированными под углом 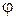, определяется формулой 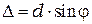, где 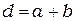, т.е.

,

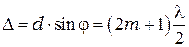где 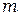= 0,± 1, ± 2, ±3,….. Отсюда следует, что направление, в котором будет наблюдаться интерференционный минимум, определяется углом 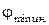по формуле:

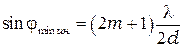. (5)

Соответственно есть направления, в которых действие одной щели из-за интерференции усиливает действие другой. Эти направления определяются условием интерференционного максимума 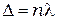, и этим направлениям соответствуют максимумы интенсивности

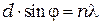
где 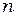=± 1, ± 2, ±3,…..

Таким образом, интенсивность на экране максимальна во всех случаях, когда разность хода между крайними лучами 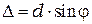равна 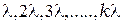, т.е. минимумы освещенности соответствуют направлениям

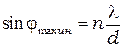, (6)

где 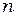- целое число.

Кривая на рис. 3б показывает распределение интенсивностей света при дифракции на двух параллельных щелях. Из кривой видно, что по оси 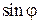возникают два характерных пространственных периода для минимумов, определяемые формулами (3) и (5), и два для максимумов – формулы (4) и (6) (на рисунке не показаны).

Расстояния между дифракционными минимумами согласно (2) зависит от ширины щели 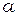. Если 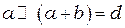, то между двумя первичными дифракционными минимумами может расположиться несколько интерференционных минимумов и максимумов, которые называют главными. Число главных интерференционных максимумов 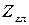определяется по формуле:

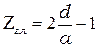. (7)

Если ширина щели 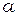значительно меньше расстояния от щели до экрана, дифракция Фраунгофера будет иметь место и при отсутствии линзы между щелью и экраном (падающая на щель волна должна быть плоской). В этом случае лучи, идущие в точку Р от краев щели, будут практически параллельны, так что все полученные ранее результаты остаются справедливыми.

Измерив на опыте по дифракционной картине от одной узкой щели ширину центрального максимума и зная длину волны источника света, можно определить ширину щели.

Схема наблюдения интерференции от двух щелей приведена на рис. 4.

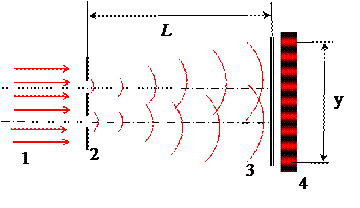
Рис. 4. Схема наблюдения интерференции (без линзы):
1 – лазерное излучение, 2 – дифракционный объект МОЛ-1; 3 – экран;
4 – вид интерференционной картин от двойной щели.

По картине интерференции от двух параллельных узких щелей, зная длину волны источника и измерив, расстояние от центра интерференционной картины до первого главного минимума и первого главного максимума, можно определить ширину щелей и расстояние между ними. Значение соответствующего 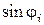определяется из геометрии опыта, полагая, что для малых углов дифракции 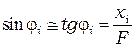, где 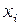- расстояние до минимума или максимума, 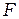- фокусное расстояние линзы.

Установка для наблюдения интерференции собрана на оптической скамье (Рис. 5) и состоит из гелий-неонового лазера ЛГ-2 (1), дифракционного объекта МОЛ-1 (2), линзы с фокусным расстоянием 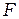= 15 см (3) и экрана (4). Вместо экрана может быть установлена видеокамера, подключённая к компьютеру.

Рис. 5. Оптическая схема установки: 1 – лазер ГН-3; 2 - дифракционный объект МОЛ-1; 3 – линза с фокусным расстоянием F; 4 – экран.

Порядок выполнения работы

Перед началом выполнения работы необходимо изучить теорию интерференции и дифракции на одиночной щели, ознакомиться с описанием дифракционного объекта МОЛ-1 в Приложении 9 и инструкцией по технике безопасности при работе с лазерными источниками света.

Проверить соответствие собранной установки схеме, показанной на рис. 5, и включить лазерный источник. Внимание! Лазерный источник включает преподаватель или лаборант.

Задание 1.

1. Получите на экране дифракционную картину от одиночной щели. Номер щели объекта МОЛ-1 задаётся преподавателем.

2. Измерьте ширину нулевого дифракционного максимума 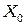(расстояние между главными дифракционными минимумами первого порядка).

3. По формуле

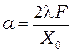(8)

рассчитайте ширину щели 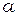. Если при получении интерференционной картины линза не используется, в формулу (8) и далее в формулах (9) и (10) вместо фокусного расстояния 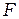подставляется 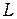- расстояние от плоскости щелей до экрана.

Задание 2

1. Повернув объект МОЛ-1 вокруг оси, получите интерференционную картину от двойной щели. Номер двойной щели объекта МОЛ-1 задаётся преподавателем.

2. Измерьте расстояние от центра интерференционной картины до центра главного интерференционного максимума первого порядка и до центра главного дифракционного минимума. Данные занесите в таблицу

Таблица 1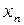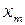

, мм.	, мм.	F, м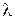м.	, нм.

3. Рассчитайте для выбранной двойной щели ширину щелей 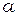и расстояние между ними 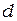по формулам:

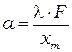, (9)

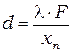. (10)

4. Рассчитайте абсолютную погрешность 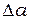измерений ширины щелей 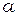по формуле:

,

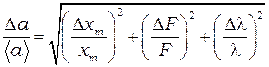где 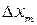, 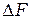и 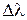- приборные погрешности измерений соответствующих величин. Для вычисления погрешности 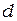используйте аналогичную формулу.

5. Запишите результат в формате:

.

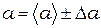
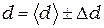Задание 3.

1. На изображении интерференционной картины от двойной щели посчитайте число главных интерференционных максимумов.

2. Используя данные задания № 2 и формулу (7) рассчитайте ожидаемое число главных интерференционных максимумов.

3. Сравните полученные результаты по пунктам 1 и 2 и сделайте выводы.

Контрольные вопросы

1.Что такое интерференция света? Какие волны называются когерентными? Как можно получит когерентные световые волны?

2. Что понимают под геометрической и оптической разностью волн?

3. Сформулируйте и выведите условия интерференционных минимумов и максимумов?

4. Какие условия нужны для получения интерференции от двух источников?

5. Дайте вывод формулы для определения расстояния между соседними интерференционными максимумами и вывод формулы для расчёта длины волны света.

6. Как будет меняться расстояния между интерференционными максимумами при изменении:

а) длины волны света;

б) расстояния между щелями;

в) расстояния между щелями и экраном.

7. Дайте объяснения понятиям длины временной и пространственной когерентности. Какими параметрами определяется длина временной и пространственной когерентности?