УСЛОВИЕ К ЗАДАНИЯМ №№ 46-51
Ниже приведены несколько видов уравнения Шредингера для общего и частного случаев:
А) 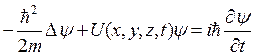 ;
;
Б) 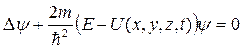 ;
;
В) 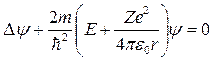 ;
;
Г) 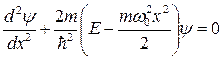 ;
;
Д) 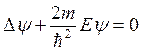 ;
;
E) 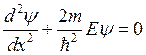 .
.
ЗАДАНИЕ № 46
Общим уравнением Шредингера является…
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
ЗАДАНИЕ № 47
Уравнением Шредингера для стационарных состояний в общем случае является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
ЗАДАНИЕ № 48
Уравнением Шредингера для электрона в водородоподобном атоме является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
ЗАДАНИЕ № 49
Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
ЗАДАНИЕ № 50
Уравнением Шредингера для частицы в трехмерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
ЗАДАНИЕ № 51
Уравнением Шредингера для частицы в одномерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками является уравнение …
ВАРИАНТЫ ОТВЕТОВ:
1) A ; 2) Б ; 3) В ; 4) Г ; 5) Д ; 6) E .
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Указание к заданиям № 46 – 51
Общее уравнение Шредингера:
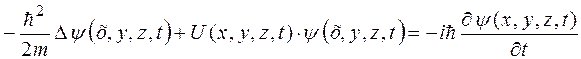 ,
,
где 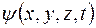 – волновая функция;
– волновая функция;
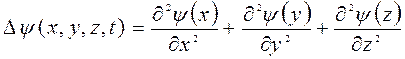 ;
;
m −масса частицы;
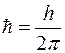 (
( 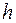 − постоянная Планка);
− постоянная Планка);
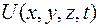 − потенциальная энергия.
− потенциальная энергия.
Для стационарного случая уравнение Шредингера:
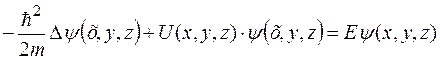 или
или
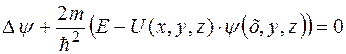 ,
,
где E – энергия частицы.
Для электрона в водородоподобном атоме функция потенциальной энергии 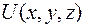 обладает центральной симметрией и задается выражением
обладает центральной симметрией и задается выражением 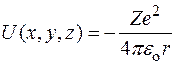 ,
,
где Z – число протонов в ядре (порядковый номер атома в таблице Менделеева);
Z e – заряд ядра ( е – величина заряда электрона);
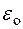 − электрическая постоянная;
− электрическая постоянная;
r – расстояние от ядра до точки (x, y, z).
Линейный гармонический осциллятор относится к одномерному случаю и потенциальная энергия задается выражением:
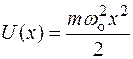 ,
,
где m − масса частицы;
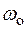 − собственная циклическая частота осциллятора;
− собственная циклическая частота осциллятора;
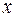 − координата частицы.
− координата частицы.
Для частиц в трехмерной или одномерной прямоугольной «потенциальной яме» с бесконечными прямоугольными стенками потенциальная энергия внутри «ямы» равна нулю ( 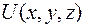 = 0 или
= 0 или 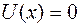 ).
).
Волновая функция
ЗАДАНИЕ № 52
На рисунках приведены картины распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками.
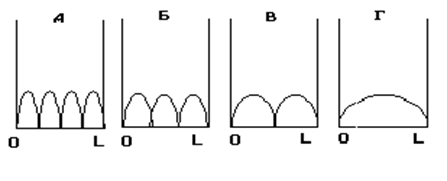
Какая из картин соответствует состоянию с квантовым числом n=3 ?
ВАРИАНТЫ ОТВЕТОВ:
1) А; 2) Б; 3) В; 4) Г; 5) Ни одна из них.
ЗАДАНИЕ № 53
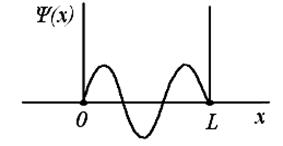
На рисунке приведен график волновой функции электрона в «потенциальной яме».
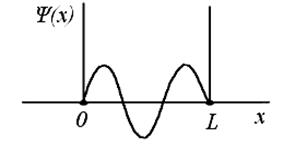
Вероятность нахождения электрона на отрезке 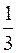 L < x <
L < x < 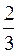 L равна...
L равна...
ВАРИАНТЫ ОТВЕТОВ:
1) 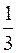 ; 2)
; 2) 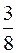 ; 3)
; 3) 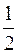 ; 4)
; 4) 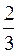 ; 5)
; 5) 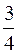 .
.
ЗАДАНИЕ № 54
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 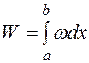 , где w − плотность вероятности, определяемая
, где w − плотность вероятности, определяемая 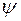 - функцией. Если
- функцией. Если 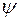 – функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке
– функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке 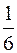 L < x <
L < x < 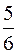 L равна:
L равна:

ВАРИАНТЫ ОТВЕТОВ:
1) 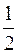 ; 2)
; 2) 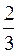 ; 3)
; 3) 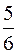 ; 4) 1 .
; 4) 1 .
ЗАДАНИЕ № 55
На рисунке приведена картина распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками. Вероятность обнаружить электрон на отрезке 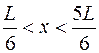 равна...
равна...
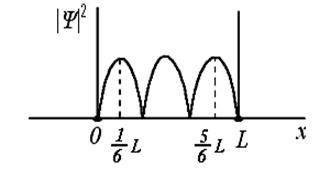 | ВАРИАНТЫ ОТВЕТОВ: 1) 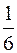 ; 2) ; 2) 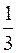 ; 3) ; 3) 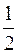 ; 4) ; 4) 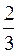 ; 5) ; 5) 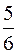 . . |
_ _ _ _ _ __ _ _ _ _ _ _ _ __ _
Указание к заданиям № 51 -55
Для частицы, находящейся в одномерной «потенциальной яме» с бесконечными стенками и плоским дном волновая функция Ψn(х) имеет следующий вид: 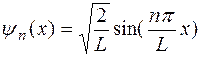 , где L – ширина «потенциальной ямы»,
, где L – ширина «потенциальной ямы»,
n – главное квантовое число (номер квантового состояния), которое характеризует энергетический уровень. В этом случае плотность вероятности 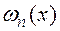 будет иметь вид:
будет иметь вид: 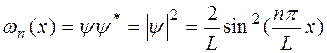 ,
,
где знак * означает комплексное сопряжение.
На участке 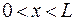 волновая функция Ψn(х) имеет n экстремумов, а функция плотности вероятности
волновая функция Ψn(х) имеет n экстремумов, а функция плотности вероятности 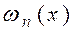 имеет n максимумов.
имеет n максимумов.
Вероятность 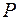 обнаружить электрон на участке (
обнаружить электрон на участке ( 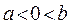 ) вычисляется по формуле:
) вычисляется по формуле: 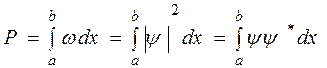 .
.
При этом вероятность 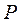 обнаружить электрон на всем участке L (
обнаружить электрон на всем участке L ( 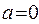 ,
, 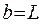 ) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой
) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой 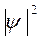 на всем участке L (
на всем участке L ( 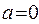 ,
, 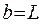 ) равна единице, а вероятность обнаружить электрон на интервале (
) равна единице, а вероятность обнаружить электрон на интервале ( 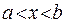 ) равна отношению площадей под кривой
) равна отношению площадей под кривой 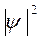 на этом интервале (
на этом интервале ( 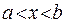 ) и на всем интервале (
) и на всем интервале ( 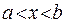 ) для
) для 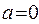 ,
, 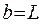 .
.
