Параллельный колебательный контур

Параллельным называется контур, элементы которого (конденсатор и катушка индуктивности) соединены параллельно друг другу и источнику питания. В радиотехнических устройствах параллельный контур питается, как правило, от источников с большим внутренним сопротивлением R_B.

Простой параллельный колебательный контур содержит конденсатор С в одной ветви и катушку индуктивности L в другой. Активное сопротивление R можно отнести к индуктивной ветви, так как потери энергии в конденсаторах, как правило, много меньше, чем в катушках индуктивности.

Параллельный контур характеризуется теми же параметрами, что и последовательный: резонансной частотой ω_р, характеристическим сопротивлением р и добротностью Q (затуханием d).

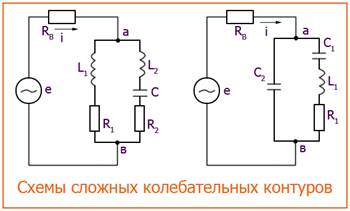
Такие контуры отличаются тем, что в них индуктивность L (или емкость С) сосредоточена не в одной ветви, а распределена по ветвям: часть индуктивности, равная pL = L₁ в одной ветви, а другая часть L₂ - L - L₁ включена в другой. Практически это достигается тем, что точка а подключения контура к генератору перемещается по исходной катушке индуктивности. Коэффициент 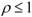называется коэффициентом включения.

Резонансная частота такого контура остается прежней:

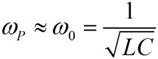
Однако резонансное сопротивление контура R’_КР отличается от величины резонансного сопротивления простого контура. Действительно, так как при резонансе реактивные сопротивления индуктивной ветви iωL₁ и емкостной ветви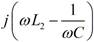

приблизительно равны по величине, но противоположны по знаку, то сопротивление контура можно записать в виде

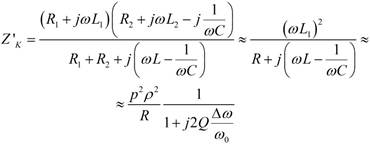
где R = R₁ + R₂ – суммарное сопротивление потерь катушки индуктивности.

Здесь мы пренебрегли в числителе малыми активными сопротивлениями R₁ и R₂ по сравнению с большими реактивными сопротивлениями 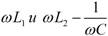.Отсюда видно, что при резонансе, когда 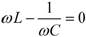, сопротивление контура

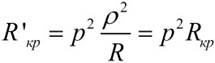
где R_КР – резонансное сопротивление простого контура.

Таким образом, изменяя коэффициент 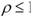, можно, не влияя на резонансную частоту контура, изменять его резонансное сопротивление. Такая мера применяется в генераторах колебаний высокой частоты с целью согласования электронной лампы с контуром.

Ширина полосы пропускания системы источник – контур при сложном включении контура может быть найдена по формуле

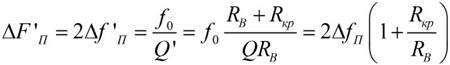
если заменить в ней R_КР на R’_КР

Аналогичные выводы справедливы и для контура с разделенной по ветвям емкостью. Резонансная частота контура 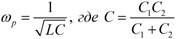– полная емкость контура. Резонансное сопротивление контура также определяется формулой

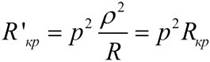
в которой, однако, коэффициент включения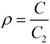

Во время наладки радиоаппаратуры бывает необходимо осуществить настройку параллельного колебательного контура на частоту питающего генератора, что достигается изменением его емкости или индуктивности. О настройке судят по величине тока в неразветвленной цепи (в этом случае в нее включают миллиамперметр) или по величине напряжения на контуре (для чего к контуру подключают вольтметр). При настроенном контуре ток в неразветвленной цепи имеет минимальную величину, а напряжение на контуре – максимальную.

Целесообразность применения того или иного способа регистрации настройки контура зависит от соотношения величин сопротивлений R_Ви R_КР. На изображении приведены зависимости i_m (f) и U_кm (f) при разных соотношениях между указанными сопротивлениями.

в случае 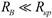напряжение на контуре U_кm (f) слабо зависит от частоты. Действительно, при 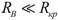в знаменателе выражения 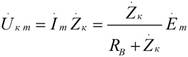можно пренебречь величиной R_В тогда приближенно 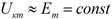Это обстоятельство затрудняет настройку контура по вольтметру. Более целесообразно в этом случае использовать миллиамперметр в неразветвленной цепи, поскольку зависимость 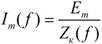имеет острый минимум.

При 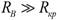, наоборот, слабо зависит от частоты ток в неразветвленной цепи. Действительно, в рассматриваемом случае в знаменателе выражения 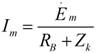можно пренебречь величиной Z_К по сравнению с R_B тогда приближенно 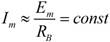. Из этого следует, что при 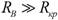пользоваться миллиамперметром (включенным в неразветвленную цепь) при настройке контура нецелесообразно. Лучший результат получается при использовании в качестве измерительного прибора вольтметра, поскольку зависимость 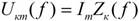имеет острый максимум при резонансе.

В случае 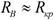можно пользоваться как миллиамперметром, так и вольтметром, поскольку зависимость i_m (f) имеет острый минимум, а U_кm (f) – острый максимум.

В мощных радиопередатчиках о настройке контура часто судят по величине тока I_кm непосредственно в контуре (для чего в контур включают амперметр). При резонансе ток I_кm достигает максимума.

Из выражения

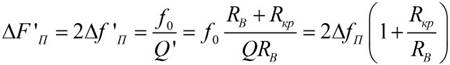
видно, что в случае 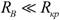ширина полосы пропускания системы контур – источник значительно превосходит ширину полосы пропускания самого контура, что в ряде случаев недопустимо. Такой случай на практике возможен в триодных резонансных усилителях напряжения, поскольку внутреннее со-противление триода 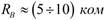, а сопротивление контура R_КР может достигать 50 – 100 ком и более. Уменьшение ширины полосы пропускания в рассматриваемом случае достигается включением колебательного контура по сложной схеме. Выбирая соответствующим образом коэффициент включения р контура, добиваются нужной величины сопротивления 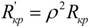и ширины полосы пропускания ΔF’_П.

Имеется простой параллельный колебательный контур с параметрами: L = 100 мкгн; С = 100 пф; R = 10 ом. Определить резонансную частоту (по точной и приближенной формулам), характеристическое сопротивление, добротность, затухание, резонансное сопротивление и ширину полосы пропускания. Внутреннее сопротивление источика, питающего контур, принять равным бесконечности (R_B = ∞).

Приближенное значение резонансной частоты вычисляем по формуле

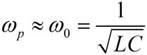
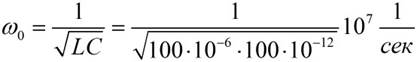
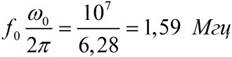
Характеристическое сопротивление

Точное значение резонансной частоты найдем по формуле:

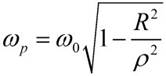
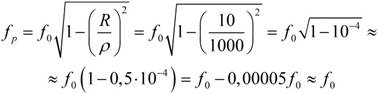
Добротность н затухание находим с учетом формулы:

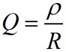
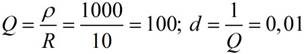
Резонансное сопротивление контура находим по формуле:

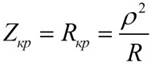
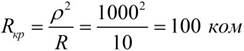
Ширина полосы пропускания контура находится при R_B = ∞ по формуле:

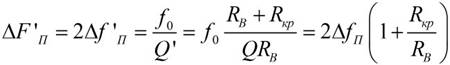
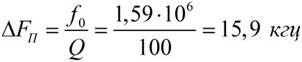
Как изменится полоса пропускания контура, рассмотренного в примере выше, если он питается от источника с внутренним сопротивлением R_B = 100 ком?

С учетом внутреннего сопротивления источника полоса пропускания выражается формулой:

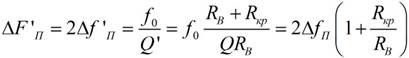
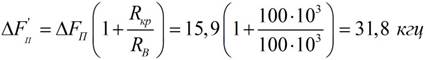
21.Реактивные двухполюсники

ДВУХПОЛЮСНИКИ