Пропускная способность

Определим пропускную способность С дискретного канала связи с помехами как максимум количества информации I(X,Y) по всевозможным распределени­ям р(х) входа канала, т.е. C = max I(X,Y). Из определения видно, что пропускная способность канала зависит только от свойств самого канала, т.е. входного и выходного алфавитов X, У и заданного на них условного распределения вероятностей р(у\х), 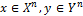,и не зависит от того источника, который подключён ко входу канала.

Пропускная способность канала имеет следующие свойства:

1. С = m a x { Н ( Y) - H(У|Х)}; 2.C≥0; 3.С = 0, тогда и только тогда, когда вход и выход канала статистически независимы. ; 4.С ≤ logm. ; 5.С = logmпри отсутствии помех в канале связи; 6.С≤ max{H(Y)} ≤ max{H(Y)}.

Помехоустойчивое кодирование.

Принципы помехоустойчивого кодирования. Кодовое расстояние. Число обнаружиеваемых и исправляемых ошибок. Коды Хемминга. Циклические коды. Обнаружение ошибок при циклическом кодировании.

Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения. По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.

Для того чтобы можно было обнаруживать и исправлять ошиб­ки, разрешенная комбинация должна как можно больше отличать­ся от неразрешенной. Если ошибки действуют независимым обра­зом (как случайные независимые события), то вероятность преоб­разования одной кодовой комбинации в другую будет тем мень­ше, чем большим числом разрядов они различаются. Если интер­претировать кодовые комбинации как точки в пространстве, то отличие выражается в близости этих точек, т. е. в расстоянии меж­ду ними.//Кодовое расстояние- количество разрядов, которыми отличаются две кодовые ком­бинации, можно принять за расстояние между ними. Для опреде­ления этого расстояния нужно сложить две кодовые комбинации по модулю 2 и подсчитать число единиц в полученной сумме. Обозначим кодовое расстояние через d. В дальнейшем интерес будет представлять только минималь­ное кодовое расстояние или расстояние Хэмминга, которое обозна­чим через d₀. Итак, у простого кода d_min=d₀=1//Рассмотрим, чему равно d₀ помехоустойчивого кода. При d₀>2 код способен обнаруживать и исправлять ошибки. При d₀=1 такой возможности нет. Нужное кодовое расстояние устанавливается введением определенного количества дополни­тельных разрядов в кодовую комбинацию. Обозначим число (кратность) обнаруживаемых ошибок через t_o, а число исправляемых ошибок — через t_u. Ошибка не обнару­живается, если одна разрешенная комбинация переходит в другую разрешенную. Следовательно, для обеспечения возможности обна­ружения всех ошибок кратностью до t₀ включительно необходи­мо, чтобы кодовое расстояние определялось неравенством: d₀ 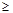t₀+1.

Число обнаруживаемых ошибок определяется минимальным расстоянием dmin между кодовыми комбинациями. Это расстояние называется хэмминговым. Если код используется только для обнаружения ошибок кратностью g₀, то необходимо и достаточно, чтобы минимальное кодовое расстояние было равно d≥2g₀+1.В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок кратностью g₀ можно записать g₀ dmin -1.

Чтобы можно было исправить все ошибки кратностью gи и менее, необходимо иметь минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu, Т.е. dmin ≥ 2gu+1 (1.13) .В этом случае любая кодовая комбинация с числом ошибок gи отличается от каждой разрешенной комбинации не менее чем в gи+1 позициях. Если условие (1.13) не выполнено, возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью не более gи можно записать: gи  (dmin-1)/2

Коды Хэмминга относятся к линейным систематическим кодам с d_o=3 и d_о==4, в которых проверочные разряды формируются линейным преобразованием информационных разрядов. Правило нахождения проверочных разрядов является основной задачей корректирующих кодов. Это правило будем определять в виде не­которого линейного оператора R. Существуют два принципиально отличных друг от друга оператора формирования:

1. bi=Ri{a_j}, i=l, 2,..., г; П. {b_r,}=R{a}_l<k.

В первом случае каждый элемент b_i проверочной части определя­ется своим оператором R_i ^.{a_j} - обозначает подмножество тех информационных элементов, которые участвуют в формировании b_i-го проверочного разряда. Таким образом, для нахождения r проверочных разрядов необходимо последовательное применение r различных операторов R_i (проверок).

2 Во втором случае оператор R действует сразу на все множе­ство разрядов информационной части, определяя тем самым в це­лом проверочную часть кодовой комбинации. Ко второму случаю относятся циклические коды. Обнаружение и исправление ошибок кодом Хэмминга сводится к определению и последующему анали­зу «синдрома». Под синдромом понимают совокупность элемен­тов, сформированных суммированием по модулю 2 принятых про­верочных элементов и вычисленных проверочных элементовпо принятым информационным элементам по тому же правилу, кото­рое применяется для их определения.

Циклические коды составляют большую группу наиболее широко используемых на практике линейных, систематических кодов. Их основное свойство, давшее им название, состоит в том, что каждый вектор, получаемый из исходного кодового вектора путем циклической перестановки его символов, также является разрешенным кодовым вектором. Принято описывать циклические коды (ЦК) при помощи порождающих полиномов G(Х)степени m = n – k, где m – число проверочных символов в кодовом слове. В связи с этим ЦК относятся к разновидности полиномиальных кодов. Операции кодирования и декодирования ЦК сводятся к известным процедурам умножения и деления полиномов. Для двоичных кодов эти операции легко реализуются технически с помощью линейных переключательных схем (ЛПС), при этом получаются относительно простые схемы кодеков, в чем состоит одно из практических достоинств ЦК.

Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок. При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.

Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью

Пример: 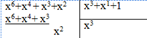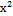→100 :ошибка в 3-ем разряде.