Раздел 1. Первое начало термодинамики

§1.1. Формулировка первого начала термодинамики.

Первое начало термодинамики выражает закон сохранения энергии для систем, в которых существенное значение имеют тепловые процессы. При сообщении термодинамической системе некоторого количества теплоты Q в общем случае изменяется ее внутренняя энергия на величину DU и система совершает работу А.

Понятие работы пришло в термодинамику из механики. Если в случае одномерного движения задана сила f, то элементарная работа определяется формулой dA=fdx, где x- обобщенная координата^*. Заметим, что уже в механике выражение для элементарной работы не является, вообще говоря, дифференциалом некоторой функции координаты x, так как сила может явно зависеть не только от x, но и от времени и от производных x по времени. Работа А, в общем случае,не определяется заданием начального и конечного состояний системы. Ее величина зависит также от способа или пути перехода системы из начального состояния в конечное. Про величины такого рода говорят, что они не являются функциями состояния. Для малого приращения такой величины используют знак d.

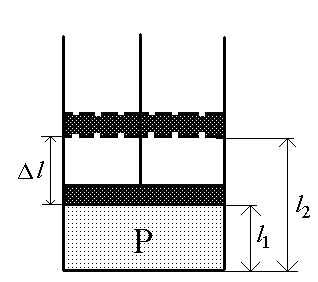Рис.1.

С другой стороны, некая функция F является функцией состояния, когда она имеет вполне определенное значение в заданном состоянии системы, не зависящее от того, каким путем или способом система в это состояние приведена. Бесконечно малое приращение этой величины является полным дифференциалом и обозначается как dF.

Рассмотрим работу, которая совершается при изменении объема, занимаемого идеальным газом. Для того, чтобы уменьшить объем, занимаемый газом, надо совершить работу по преодолению сил давления газа. Представим себе газ, заключенный в цилиндрическом объеме с поршнем, движение которого изменяет объем газа. Найдем выражение для работы, совершаемой газом при изменениях его объема. Предположим, что газ, находящийся в цилиндрическом сосуде под поршнем, изобарно расширяется от V₁ до V₂ (рис.1). При этом поршень перемещается на расстояние Dl=l₁-l₂, а объем газа изменяется на DV=V₂-V₁.

*Обобщенные координаты - независимые параметры любой размерности, число которых равно числу степеней свободы механической системы и которые однозначно определяют положение системы. Обобщенные координатами пользуются для решения задачи, когда система подчиняется связям, налагающим ограничения на ее движение.

На поршень, площадь поперечного сечения которого S, со стороны газа действует сила F=pS. Так как направление этой силы совпадает с направлением перемещения поршня, то работа, совершаемая газом равна:

A=FDl=pSDl=pDV.

(1.1)

Принято, что работа, производимая внешними силами над газом, имеет отрицательный знак, а работа, производимая газом при увеличении его объема, имеет положительный знак. Если при изменении объема газа его давление изменяется, то следует записать элементарную работу, соответствующую достаточно малому изменению объема dV:

dA=pdV.

(1.2)

Проинтегрировав (1.2), получим работу, совершаемую газом

.

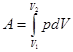(1.3)

В молекулярной физике энергия, которая связана с движением частиц системы (например, молекул) и взаимодействием их между собой, называется внутренней. Таким образом, к внутренней энергии не относится кинетическая энергия, связанная с движением центра масс системы, то есть движения совокупности частиц как целого, и энергия, заключенная внутри частицы.

Для определения внутренней энергии идеального газа необходимо использовать теорему о равнораспределении энергии по степеням свободы. В статистической физике число степеней свободы (i) соответствует независимым обобщенным координатам, определяющим полную энергию или функцию Гамильтона системы. При этом каждый атом молекулы будет заменяться материальной точкой, не имеющей протяженности. Энергия такой молекулы может быть записана в виде: e=e_пост+e_вращ+e_кол, где e_пост, e_вращ и e_кол – соответственно энергии поступательного, вращательного и колебательного движений. Поступательное движение многоатомной молекулы в пространстве ничем не отличается от поступательного движения одноатомных молекул, поскольку сводится к движению центра тяжести системы, положение которого задается тремя координатами x, y и z. Они определяют три степени свободы поступательного движения. Количество степеней свободы, связанные с вращательным движением, задаются количеством взаимно перпендикулярных осей, вокруг которых может вращаться многоатомная молекула, меняя свое положение в пространстве. Поэтому для одноатомного газа i=3, так как говорить о вращении вокруг какой-либо оси для одного атома в модели идеального газа не имеет смысла, для двухатомной молекулы i=5. Колебание же атомов в молекуле, происходит вдоль линий, их соединяющей. На одну колебательную степень свободы приходится в среднем энергия вдвое больше, чем на одну степень поступательного или вращательного движения, так как энергия колебательного движения складывается из одинаковых средних значений кинетической и потенциальной энергий. В условиях статистического равновесия на каждую степень свободы поступательного и вращательного движения системы приходится одинаковая средняя энергия kT/2.

Классическая теория, в основном, правильно описывает тепловые явления в газе в некоторых узких интервалах температур, однако температурная зависимость теплоемкости в целом, наблюдаемая в эксперименте, ведет себя далеко не так, как предсказывает классическая теория (см. рис.2). На рисунке приведена качественная зависимость молярной теплоемкости С_V от температуры для аргона (Ar) и водорода (H₂). Лишь для одноатомных газов (Ar) теплоемкость С_V в широком диапазоне температур постоянна и соответствует, как и показывает теория, трем степеням свободы (i = 3) (за исключением температур, близких к абсолютному нулю). При температурах T < 100K водород ведет себя как одноатомный газ с i = 3. Затем число степеней свободы как бы непрерывно растет и достигает значения i= 5 при Т = 400К. Это несоответствие теории и эксперимента было понято только с появлением квантовой теории теплоемкости, основанной на представлении о дискретности вращательных и колебательных уровней молекул. При низких температурах наблюдается только поступательное движение молекул. С ростом температуры все большее число молекул вовлекается во вращательное движение. Если средняя тепловая энергия kT заметно превышает энергию первого вращательного уровня, в молекуле возбуждено уже много вращательных уровней. В этом случае дискретность уровней становится несущественной и теплоемкость равна своему классическому значению.

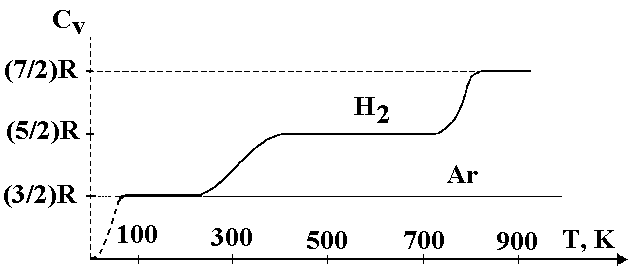
Рис.2.

Аналогичная ситуация имеет место и с возбуждением колебательных степеней свободы. Равнораспределение действительно только тогда, когда тепловая энергия k_BT намного больше, чем интервал, потому что в противном случае средние значения энергии и теплоёмкости, приходящиеся на определённые степени свободы меньше чем величины, полученные с использованием теоремы о равнораспределении. Говорят, что степень свободы выморожена, если тепловая энергия намного меньше, чем интервал между соседними квантовыми уровнями энергии. Например, теплоёмкость твёрдого тела уменьшается при низких температурах, поскольку различные типы движения становятся вымороженными, вместо того, чтобы остаться постоянными, как следует из теоремы о равнораспределении энергии по степеням свободы.

Внутренняя энергия идеального газа, содержащего N молекул, определяется выражением:

,

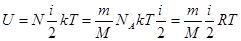(1.4)

где i=i_пост+i_вращ+2·i_кол количество степеней свободы молекулы, k – постоянная Больцмана, N_A –число Авогадро, M –молярная масса, m – масса вещества, Т – температура, R – универсальная газовая постоянная.

Ниже будет показано, что

.

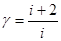(1.5)

Тогда выражение для внутренней энергии идеального газа принимает вид:

.

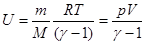(1.6)

Закон сохранения энергии для тепловых процессов может быть записан в следующей очевидной форме:

.

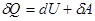(1.7)

Закон сохранения энергии в виде (1.7) называется первым началом термодинамики. Так же как и в механике, закон сохранения энергии не может предсказать направление развития процесса. Также как и работа, теплота не является функцией состояния системы.

В теоретических методах термодинамики широко используются модельные представления. Это так называемые квазистатические или квазиравновесные процессы, т.е. идеализированные процессы, состоящие из непрерывно следующих друг за другом состояний равновесия. Состояние называется равновесным, в котором каждый макроскопический параметр имеет одно и то же значение во всех точках системы и остается неизменным сколь угодно долго, если не меняются внешние условия.

В термодинамике наиболее часто встречаются следующие квазистатические процессы: изобарный процесс – это процесс, происходящий при постоянном давлении (Р=const); изохорный процесс – процесс, осуществляемый при постоянном объеме (V=const); изотермический процесс – это процесс, осуществляемый при постоянной температуре (T=const); адиабатный процесс – это процесс, при котором отсутствует теплообмен с окружающей средой. Выражения первого начала термодинамики для каждого из перечисленных процессов приведены в таблице.

Таблица. Запись первого начала термодинамики для различных процессов.

Название процесса	DQ	A	DU
P=const Изобарический		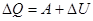A=p(V2-V1)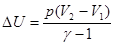
Т=const Изотермический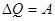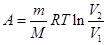
V=const Изохорический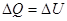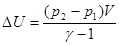
DQ=0 Адиабатический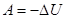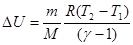

Задача. 1.1. Молекулы азота занимают объем V₁ =2 м³ и находится под давлением p₁=1 атм. Газ нагревают, причем нагрев ведут сначала при постоянном объеме до давления p₂=5 атм, а затем при постоянном давлении до объема V₂=4 м³. Масса азота 3 кг. Газ идеальный. Определить изменение внутренней энергии газа, совершенную им работу, количество тепла, переданное газу.

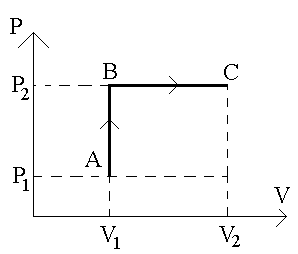
Решение. Задачи такого типа решать проще, если все переходы газа из одного состояния в другое представлены графически. На рисунке оба процесса перехода изображены в системе координат PV. Прямая AB – изохора, идет нагревание газа от T₁ до T₂ c соответствующим увеличением давления от p₁ до p₂ при постоянном объеме V₁. В этом процессе происходит увеличение внутренней энергии газа целиком за счет тепла (см. таблицу). Прямая BC – изобара. Ей соответствует повышение температуры, а, следовательно, и изменение внутренней энергии. Кроме того, газ, расширяясь, совершает работу.

Полное изменение энергии складывается из изменения энергии DU₁ на участке AB и изменения энергии DU₂ на участке BC

, .

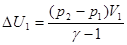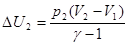Общее изменение внутреннее энергии есть сумма DU₁+DU₂:

.

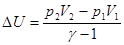Работа, совершаемая газом, графически определяется площадью под кривой ABC в системе координат PV, и складывается из работ на участках AB и BC. В нашем случае, работа на участке AB не производится, следовательно, вся работа над газом будет определяться работой на участке изобарического процесса BC

.

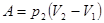Количество поглощенного тепла определяется по первому началу термодинамики

.

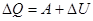Подставив числовые данные в формулы, определим соответственно

A= 1,01·10⁶Дж; DU=5·10⁶Дж; DQ=6,01·10⁶Дж.

Задачи для самостоятельного решения:

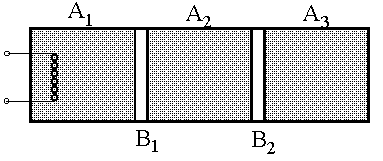
Задача 1.2.Цилиндр с теплоизолированными (адиабатными) секциями разделен на три отделения A₁, A₂, A₃ (см. рисунок) теплоизолирующим поршнем В₁ и теплоизолирующим поршнем В₂. Поршни могут скользить вдоль цилиндра без трения. В каждой из частей цилиндра содержится 0,1 моль идеального двухатомного газа. Вначале давление газа во всех частях p₀=10⁵ Па и температура Т=300К. Затем газ в отделении А₁ медленно нагревают до тех пор пока температура в отделении А₃ не станет Т₃=340К. Найти объем в конечном состоянии и изменение внутренней энергии газов для каждого отделения, а также полную энергию, которая была сообщена газу в отделении А₁ при нагревании.

Ответ: V₁=3,837·10^-3 м³, V₂=V₃=3,837·10^-3м³; DU₁=862,2Дж, DU₂=DU₃=83,1Дж.

Задача 1.3.Два моля идеального газа при давлении p₁ и температуре Т изотермически сжимают до давления p₂. Определите работу, совершаемую над газом, в процессе его сжатия.

Ответ: .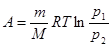

§ 1.2. Теплоемкость.

Теплоемкостью тела C называется отношение бесконечно малого количества тепла dQ, полученного телом, к соответствующему приращению dT его температуры.

.

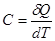(1.8)

Когда масса тела равна единице, теплоемкость называют удельной и обозначают прописной буквой с. Молярная теплоемкость – теплоемкость моля вещества. Обычно эту величину обозначают заглавной буквой С.

Теплоемкость зависит от условий, в которых телу сообщается теплота и изменяется его температура. Особое значение имеют теплоемкости при постоянном объеме и постоянном давлении, обозначаемые символами C_V и C_P. Если объем остается постоянным, то dV=0, работа не совершается, и, следовательно, для идеального газа

.

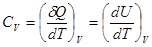(1.9)

Если же постоянно давление, то

,

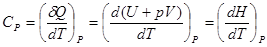(1.10)

где H=pV+U функция состояния, называемая энтальпией.

Изобарный, изохорный, изотермический и адиабатный процессы являются частными случаями политропного процесса, т.е. процесса, в котором теплоемкость является постоянной величиной. Уравнение политропы в переменных p, V имеет вид:

,

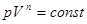(1.11)

где n – показатель политропы, равный 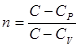. Для изохорического процесса уравнение политропического процесса в переменных p, T имеет вид: 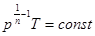. А так как теплоемкость С=С_V в этом случае, 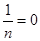. Уравнение политропы для изохорического процесса принимает вид: p/T=const.

Задача. 1.4. Установите соотношения между молярными теплоемкостями C_P и С_V для идеального газа.

Решение. Пусть один моль идеального газа находится в цилиндре с поршнем. Закрепив поршень, повысим температуру газа на dT. Поскольку объем газа остается постоянным, то количество тепла, необходимое для такого нагревания, равно (dQ)_V=C_VdT. Так как при этом не производится работа, то это тепло равно приращению внутренней энергии газа С_VdT=dU. Проведем теперь с тем же газом другой опыт. Пусть начальное состояние будет тем же самым, что и в предыдущем опыте, но поршень не закреплен, а может свободно перемещаться под постоянным внешним давлением p. По определению теплоемкости C_P для повышения температуры газа на величину dT требуется тепло (dQ)_Р=C_РdT. При этом газом будет совершена работа dА=pdV. Так как давление постоянно, то для моля идеального газа из уравнения Менделеева – Клапейрона:

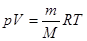(1.12)

следует, что dA=d(pV)= 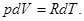А так как внутренняя энергия газа зависит только от температуры, то она изменится на столько же, на сколько и в предыдущем опыте. Таким образом: 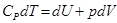. Подставив вместо dU=RdT, получаем

.

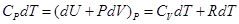Сократив правую и левую часть уравнения на конечную величину dT, получим уравнение Роберта Майера

.

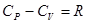(1.13)

Для одного моля газа с i степенями свободы внутренняя энергия из (1.4) U=iRT/2, тогда C_V= iR/2. Так как С_P=R+C_V, то можно найти отношение C_p/C_V, приведенное ранее в (1.5).

Задача 1.5. Найти уравнение адиабатического процесса для идеального газа, выразив его через p и V.

Решение. При адиабатическом процессе теплота системе не сообщается и не выводится. 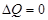. Тогда изменение внутренней энергии равно работе совершаемой над газом.

.

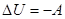Продифференцируем правую и левую часть равенства.

.

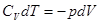С другой стороны, продифференцировав уравнение для одного моля идеального газа, получаем, что:

.

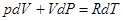Выразим dT из последнего выражения, подставим R из (1.13), имеем:

.

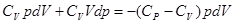После раскрытия скобок получаем:

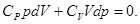
Разделим правую и левую часть на C_VVp, и введя обозначение C_p/C_V=g.

Получаем дифференциальное уравнение с разделяющимися переменными.

.

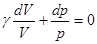Решив его, получаем уравнение Пуассона для адиабатических процессов

.

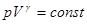(1.14)

Уравнение Пуассона является частным случаем политропического процесса, где n=g.

Задача.1.6.Молярная теплоемкость идеального газа при некотором процессе изменяется по закону 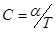, где a - постоянная величина. Найти уравнение, связывающие параметры p и V в этом процессе.

Решение. Используем определение молярной теплоемкости для произвольного процесса: 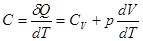. С другой стороны, по условию задачи 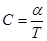. И получаем:

.

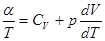В уравнении, описывающем процесс, меняются две величины: давление и объем. Выразив давление для одного моля идеального газа через объем и температуру из уравнения Менделеева-Клапейрона ( 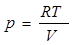) и подставив в предыдущие уравнение эти величины, получим дифференциальное уравнение .

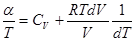Разделим обе части выражения на RT и умножим на dТ. Перенесем слагаемые, содержащие температуру в левую часть, а слагаемые, содержащие объем в правую, и получаем дифференциальное уравнение с разделяющимися переменными:

.

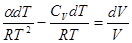Интегрируя правую часть по объему, левую по температуре, получаем:

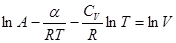, где А – const;

.

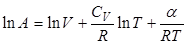Потенцируем правую и левую часть этого выражения:

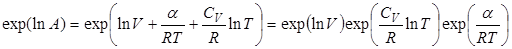и получаем:

.

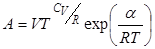Принимая во внимание, что ,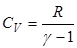

.

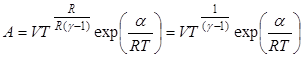Из уравнения Менделеева-Клапейрона для одного моля газа следует, что 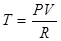, тогда:

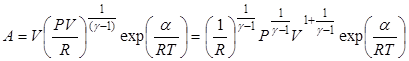, и

получим уравнение, связывающие параметры P и V в этом процессе:

.

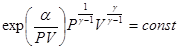Возводя все выражение в степень (g-1), получим ответ

.

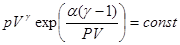Задачи для самостоятельного решения:

Задача. 1.7. Чему равны удельные теплоемкости C_V и C_P идеального двухатомного газа, если плотность этого газа при нормальных условиях равна 1,43 кг/м³?

Ответ: C_V=650 Дж/(кг·К), C_P=906 Дж/(кг·К).

Указание: Если в задаче газ находится при нормальных условиях, то подразумевается, что известны давление p₀=101325Па=760 мм ртутного столба и температура Т=273,15К (0⁰С).

Задача 1.8.Найти уравнение процесса изменения состояния идеального газа, при котором его молярная теплоемкость меняется с температурой по закону C=aT.

Ответ: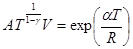

Задача 1.9. Один моль некоторого идеального газа изобарически нагрели на DТ=72К, сообщив ему количество тепла Q=1,6 кДж. Найти приращение его внутренней энергии и величину g=С_p/C_V.

Ответ: DU=Q-RDT=1 кДж; g=Q/(Q-RDT)=1,6.

Задача 1.10. Вычислить g для газовой смеси, состоящей из n₁=2 моля кислорода и n₂=3 моля углекислого газа. Газы считать идеальными.

Ответ: g=[n₁g₁(g₂-1)+n₂g₂(g₁-1)]/[n₁(g₂-1)+n₂(g₁-1)]=1,33

Газ Ван-дер-Ваальса.

Перейдем к изучению реальных газов. Отступление от законов идеального газа в них связано с тем, что между молекулами газа действуют силы, которые в теории идеальных газов во внимание не принимаются. Если химическое соединение не образуется, то силы взаимодействия между молекулами и атомами называются молекулярными силами. Полное понимание природы молекулярных и химических сил возможно только в рамках квантовой механики. На далеких расстояниях молекулярные силы являются силами притяжения. Эти силы притяжения называют также силами Ван-дер-Ваальса по имени голландского ученого заложившего основы молекулярной теории реальных газов. Сила межмолекулярного притяжения, имеет три составляющие. Они обладают несколько отличной физической природой, отличаются по величине, но их потенциал зависит от расстояния между молекулами одинаково – как 1/r⁶. Ориентационноенаиболее сильноевзаимодействие (или сила Кизома) возникает между полярными молекулами, которые сами по себе имеют электрический дипольный момент. Индукционное взаимодействие (или сила Дебая) возникает между полярной и неполярной молекулами. Дисперсионное самое слабое взаимодействие (или сила Лондона) является наиболее распространенным, т.к. в нем участвуют и неполярные молекулы, и имеет квантово-механическую природу. Модельные представления о дисперсионном взаимодействии основаны на флуктуациях распределения электронной плотности, благодаря которым даже у неполярных молекул возникают ненулевые мгновенные дипольные (или высшие мультипольные) моменты. Эти моменты дополнительно поляризуют распределения электронной плотности соседних молекул. Ненулевое теперь уже поле второй молекулы поляризует первую. Потенциал в этой своеобразной системы с "положительной обратной связью" рассчитывается аналогично индукционному взаимодействию. Зависимость потенциала диполь-дипольного, поляризационного и дисперсионного взаимодействий от расстояния может быть представлена в виде ряда по степеням обратного расстояния, причем определяющий вклад обусловлен шестой степенью.

Силы Ван-дер-Ваальса начинают проявляться на расстояниях двух-трех диаметров молекулы. В результате между молекулами возникнут силы притяжения. Однако, когда молекулы подойдут «вплотную» друг к другу, между соприкасающимися электронными оболочками возникнут огромные силы отталкивания квантово-механической природы (кулоновское отталкивание). На рис.3 изображена примерная зависимость потенциальной энергии взаимодействия молекул от расстояния между их центрами r. Кривая потенциальной энергии U=U(r) имеет минимум U_min в положении равновесия при r=r₀. Силы взаимодействия между молекулами больше нуля при r<r₀ (действуют силы отталкивания), при r>r₀ действуют силы притяжения. Структура любой совокупности молекул и агрегатное состояние вещества будут существенно зависеть от соотношения величин kT и ½U_min½.

А) В предельном случае низких температур, когда kT<<½U_min½, молекулы или иные частицы расположены в определенном порядке, образуя т.н.

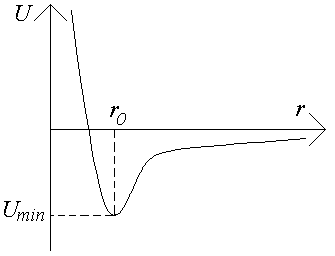Рис.3.

кристаллическую решетку. Вещество будет находиться в кристаллическом состоянии. Тепловые движения будут проявляться в виде колебаний частиц в узлах кристаллической решетки.

Б) В пределе высоких температур, когда kT>½U_min½, интенсивное тепловое движение будет препятствовать сближению молекул. Вещество при этом будет находиться в газообразном состоянии. При более высоких температурах может происходить так называемая ударная ионизация молекул или образовываться новые частицы ( молекулы из атомов и т.п.).

В) При промежуточных температурах, когда kT»½U_min½, благодаря тепловому движению молекулы будут непрерывно перемещаться в пространстве, обмениваясь местами, но, не отходя от соседей на расстояния, заметно превышающие величину r₀. Вещество будет находиться в жидком агрегатном состоянии.

Уравнения состояния реальных газов должно учитывать конечное значение собственного объема молекул и взаимное притяжение их друг к другу. Ван-дер-Ваальс предложил в уравнения состояния для одного моля реального газа включить не объем сосуда, а объем не занятый молекулами, т.е. величину (V_m-b), где V_m – молярный объем. Постоянная b определяет ту часть объема, которая недоступна для движения молекул вследствие их конечного размера. Для нахождения величины b предположим, что в сосуде имеются лишь две молекулы, центры которых не могут сблизиться на расстояние, меньше s. Таким образом, для центра каждой молекулы недоступным оказывается объем шара радиусом s, равный 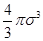, а в расчете на одну молекулу – объем, вдвое меньший. Исходя из этого примерного расчета, недоступный объем для N_A молекул

.

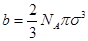(1.15)

Окружим каждую молекулы сферой молекулярного действия. Если эта сфера находится внутри газа, то силы, действующие на рассматриваемую молекулу со стороны окружающих молекул, в среднем уравновешиваются. Но этого не произойдет, если молекула находится вблизи газа со стенкой. Появляется избыток молекул, тянущих рассматриваемую молекулу внутрь газа, над молекулами, тянущими ее наружу. Таким образом, вблизи стенки возникает пристеночный слой газа, толщина которого равна радиусу сферы молекулярного действия. Вследствие притяжения ударяющих о стенку молекул всеми остальными молекулами газа давление, оказываемое газом на стенку, уменьшается на величину p_i. p_i называется внутренним или молекулярным давлением. Поскольку силы взаимодействия молекул очень быстро убывают с расстоянием, то следует учитывать притяжение одного лишь соседнего слоя. Сила этого притяжения (рассчитанная на единицу площади) пропорциональна концентрации молекул в обоих слоях или обратно пропорциональны объему газа 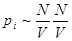. Введя коэффициенты пропорциональности можно перейти к равенству для одного моля газа:

,

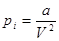(1.16)

где а – постоянная, характерная для рассматриваемого газа. Тогда уравнение состояния для моля газа Ван-дер-Ваальса будет иметь вид:

.

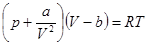(1.17)

Внутренняя энергия газа Ван-дер-Ваальса состоит из двух частей: кинетической энергии поступательного и вращательного движения молекул Е_К и потенциальной энергии их взаимодействия Е_П. Предполагая, что к реальному газу по-прежнему применима теорема о равномерном распределении энергии по степеням свободы, можно для расчета Е_К воспользоваться формулой, полученной для одного моля идеального газа:

.

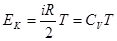(1.18)

Потенциальная энергия взаимодействия молекул определяется следующим образом. При расширении газа силы внутреннего или молекулярного давления 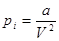совершают работу, которая равна

.

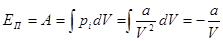(1.19)

Окончательно, внутренняя энергия одного моля реального газа равна:

.

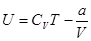(1.20)

Задача. 1.11. Прохождение газа через пористую перегородку (адиабатическое дросселирование) в теплоизолированной трубе сопровождается расширением и изменением температуры газа (эффект Джоуля-Томсона). Если до расширения газ считать ван-дер-ваальсовским, а после расширения – идеальным, то соответствующее приращение температуры газа

.

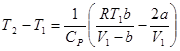(1.21)

Получите эту формулу, применив первое начало термодинамики к молю газа, проходящему через перегородку. Процесс считать адиабатическим. (Это интегральный эффект Джоуля-Томсона).

Решение:

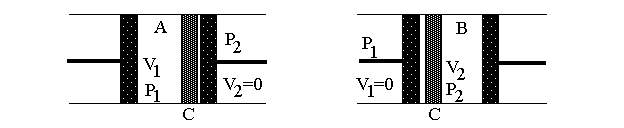
Рис.4а Рис.4б

На рисунке изображена схема расширения газа в адиабатических условиях. На рис.4а – начальное состояние системы, на рис.4б – конечное. В середине цилиндра, помещенного в адиабатическую оболочку, находится перегородка С (узкая щель, пористое тело, дроссель и т.п.), препятствующая быстрому прохождению газа. Из части 1 поршнем через перегородку продавливается газ, в результате чего объем газа меняется от V₁ до нуля. При этом в части 2 перемещается поршень, и объем газа при постоянном давлении изменяется от нуля до V₂. Так как величины давления p₁ и p₂ постоянны, то в части 1 газ совершает работу А₁=-p₁V₁, а в части 2 A₂=p₂V₂. Будем считать, что внутренняя энергия системы изменилась на величину U₂-U₁.

Запишем для этого процесса первое начало термодинамики

Q=U₂-U₁+p₂V₂-p₁V₁.

Так как процесс адиабатический (Q=0), то имеем

U₁+p₁V₁=U₂+p₂V₂.

Для одного моля реального газа ; .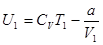

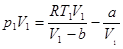Для одного моля идеального газа U₂=C_VT₂; p₂V₂=RT₂.

.

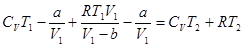Преобразуем выражение следующим образом:

,

.

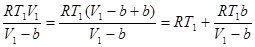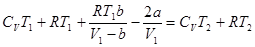Отсюда следует, что:

.

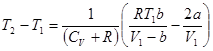Из этого условия ясно, что расширение реального газа без теплообмена должно сопровождаться изменением его температуры.

Температура реальных газов в таком процессе может как понижаться: DT<0 (положительный эффект Джоуля-Томсона), так и повышаться: DT>0 (отрицательный эффект Джоуля-Томсона). Температура, при которой происходит изменение знака эффекта Джоуля-Томсона, называется температурой инверсии:

.

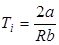(1.22)

Газ, имеющий температуру выше температуры инверсии, нагревается, ниже – охлаждается. Температура инверсии зависит от давления и свойств газа, поэтому при одной и той же температуре некоторые газы могут нагреваться, а другие охлаждаться. Например, при комнатной температуре и невысоком давлении воздух при адиабатическом дросселировании в процессе Джоуля-Томсона охлаждается, для достижения такого же эффекта водород следует охладить до 200К, а гелий до 40К.