Интерференция в тонких пленках

Цель работы: изучение явления интерференции, определение радиуса кривизны стеклянной линзы и длины волны света при наблюдении колец Ньютона.

Приборы и принадлежности

1. лабораторный комплекс ЛКО-1А

2. объект 46 «кольца Ньютона».

Теоретическое введение

Интерференцией светаназывается явление наложения коге­рентных световых волн , в ре­зультате которого происходит пространственное перераспределение светового потока, то есть возникновение максимумов и минимумов интенсивности.

Когерентность – это согласованное протекание во вре­мени и пространстве нескольких колебательных или волновых процессов. Так, две волны являются когерентными, если выполняются следующие условия:

а) частоты волн равны n₁=n₂; б) разность фаз волн в течение всего вре­мени их взаимодействия не изменяется, то есть j = j₁ - j₂ = const.

Строго когерентными могут быть только монохроматические волны – неограниченные в пространстве волны с постоянной во времени частотой, амплитудой и начальной фазой.

Излучение обычного источника света представляет собой прерыви­стое спонтанное излучение света атомами в виде отдельных кратковремен­ных импульсов (волновых цугов), длительность которых не превышает

10^-8с, а начальные фазы изменяются совершенно хаотично. Вследствие этого свет, испускаемый макроскопическим источником, не является мо­нохро­матическим.

Примером интерференции света, наблюдающейся в естественных ус­ловиях, может служить радужная окраска тонких пленок (мыльных пузы­рей, пленок масла или нефти на поверхности воды и т.п.). Образование частично когерентных волн, интерферирующих при наложении, в этом случае происходит вследствие отражения падающего на пленку света от её верхней и нижней поверхностей. Оптическая разность хода интерфери­рующих волн изменяется при переходе от одних точек на поверхности клина к другим в соответствии с толщиной пленки. В плёнке, имеющей вид клина, области одинаковой толщины вытянуты вдоль ребра клина и в соответствии с этим будут расположены тёмные и светлые полосы. Каждая из полос образуется за счет отражений от мест пластинки с одинаковой толщиной, поэтому интерференционные полосы получили название «по­лос равной толщины». Полосы равной толщины локализованы вблизи пластинки – над ней, либо под ней. В случае нормального падения лучей на пластинку полосы равной толщины локализуются на верхней поверхно­сти пластинки.

Интерференцию на клине впервые наблюдал И.Ньютон. Он исследовал цвет тонкой прослойки воздуха, заключённого между плоскопараллельной стеклянной пластинкой и выпуклой поверхностью линзы с радиусом кривизны около 10 метров (рис.1).

Рис.1. К расчету радиусов «колец Ньютона»

Роль тонкой пленки выполнял воздушный зазор, толщина которого hочень мала и уменьшается по мере приближения к точке соприкосновения линзы со стеклом. При нормальном падении сверху на такую систему монохроматического света интерференция наблюдается при отражении от верхней поверхности прослойки на границе стекло-воздух и от нижней поверхности на границе воздух-стекло. В отраженном свете оптическая разность хода с учетом того, что показатель преломления воздуха n = 1, а угол падения α = 0, равна

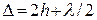(1)

(волна, отраженная от плоской поверхности линзы, при этом не учи­тывается, так как оптическая разность хода между ней и волнами, отра­женными от границ воздушного зазора, больше длины когерентности). По­скольку оптическая структура обладает осевой симметрией, наблюдаю­щиеся интерференционные полосы принимают вид концентрических ко­лец: в центре – темное пятно, окруженное светлой концентрической поло­сой, которая постепенно переходит в темную, затем снова сменяется свет­лой и т. д. По мере увеличения толщины прослойки воздуха расстояние между соседними минимумами и максимумами уменьшается. В проходя­щем свете центральное пятно – светлое, следующее кольцо темное и т.д. Эта интерференция получила название «кольца Ньютона». Если свет па­дает на такую систему под каким-либо углом, то интерференцион­ные линии имеют вид эллипсов. Из рисунка 1 видно, что

, (2)

где R – радиус кривизны линзы; r – радиус окружности, всем точкам которой соответствует зазор h. Величиной h² ввиду её малости по сравнению с 2Rh в выражении (2) можно пренебречь, тогда для толщины зазора полу­чим h = r²/2R. Оптическая разность хода лучей будет равна

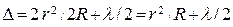. (3)

Из (3) и условий интерференционных максимумов 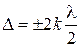и мини­мумов получим для радиуса k-го светлого кольца

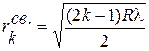, k =1,2,3… (4)

и для тёмного кольца

, k = 0,1,2,3… (5)

Отметим, что чем больше k (порядковый номер кольца), тем меньше различие между радиусами соседних колец, то есть тем ближе расположены кольца друг к другу. Измеряя радиусы соответствующих колец, можно определить длину волны и, наоборот, по известной l найти радиус кривизны линзы. Более верный результат, исключающий систематическую погрешность, получится, если вычислять R (или λ) по разности радиусов двух колец r_k и r_n.В этом случае формула для вычисления будет иметь вид

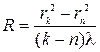, (6)

где k и n номера колец. При освещении белым светом центральное темное пятно будет окружёно системой цветных колец, соответствующих интер­ференционным максимумам света с различными значениями длин волн. Число наблюдаемых колец при этом невелико, так как при больших k происходит наложение колец разных длин волн, и они расплываются.