Динаміка обертального руху твердого тіла

· Момент сили відносно центра обертання:

.

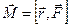· Момент імпульсу матеріальної точки відносно центра обертання:

,

де 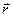– радіус-вектор, проведений з центра координат (центра обертання) до точки прикладення зовнішньої сили 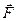, або до матеріальної точки, імпульс якої .

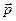· Момент сили та момент імпульсу відносно осі:

,

,

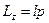де 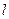– плече сили, тобто найкоротша віддаль від точки до осі обертання;

· Момент інерції матеріальної точки відносно осі обертання:

,

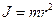де 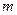– маса точки, 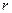– віддаль від точки до осі обертання.

· У випадку неперервного розподілу точкових мас у твердому тілі момент інерції вираховується інтегралом:

,

де 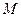– маса тіла.

· Моменти інерції найпростіших геометричних фігур, при умові рівномірного розподілу маси по об’єму тіла, мають такі визначення:

1. Однорідний стрижень, відносно осі, що проходить через його середину і перпендикулярна до нього:

,

де 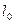– довжина стрижня, а m – його маса.

2. Тонкий обруч радіусом :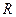

,

де 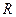– радіус обруча; m – маса обруча.

3. Диск, циліндр, відносно осі, що проходить через їх центр мас перпендикулярно до основи:

,

де 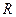– радіус диска (циліндра); m – масса диска (циліндра).

4. Суцільна куля, відносно осі, що співпадає з діаметром:

,

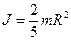де 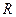– радіус кулі; m – масса кулі.

· Момент інерції тіла відносно довільної осі обертання (теорема Штейнера):

.

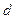де – момент інерції даного тіла відносно осі, що проходить через центр мас і паралельна до заданої осі обертання; – віддаль між осями; 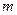– маса тіла.

· Момент імпульсу твердого тіла при обертальному русі відносно певної осі:

.

· Основний закон динаміки обертального руху:

,

де 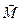– сумарний момент зовнішніх сил, прикладених до тіла.

При умові незмінності моменту інерції тіла відносно осі обертання, тобто , закон динаміки обертального руху можна записати у виді:

,

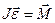де 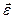– кутове прискорення.

· Закон збереження моменту імпульсу.

При умові відсутності неконсервативних сил всередині замкненої системи матеріальних точок, в тому числі, і для твердого тіла, виконується закон збереження моменту імпульсу :

.

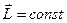· Робота постійного моменту сил 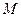при обертанні тіла на кут :

.

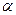· Кінетична енергія тіла, що обертається:

.

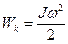· Тверде тіло в ролі фізичного маятника має період коливань:

,

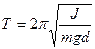де 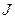– момент інерції відносно осі підвісу; 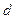– віддаль від осі підвісу до центра мас; – прискорення вільного падіння.

3.1. Знайти момент інерції 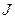та момент імпульсу 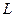земної кулі відносно осі обертання. Радіус земної кулі 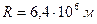; середня густина Землі .

3.2. Дві кулі однакової маси і однакового радіуса закріплені на кінцях невагомого стрижня. Віддаль між кулями 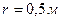.Знайти момент інерції 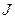системи відносно осі, що є перпендикулярною до стрижня і співпадає з діаметром однієї з куль.

3.3. По дотичній до однорідного диска радіусом прикладена сила . При обертанні на диск діє ще момент сил тертя 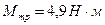. Знайти масу диска 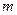, якщо відомо, що диск обертається з кутовим прискоренням .

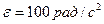3.4. Однорідний стрижень довжиною 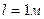і масою обертається у вертикальній площині навколо горизонтальної осі, що проходить через середину стрижня. З яким кутовим прискоренням обертається стрижень, якщо на нього діє момент сил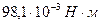

3.5. Однорідний диск радіусом і масою обертається навколо осі, що проходить через його центр перпендикулярно до його площини. Кутова швидкість диска задається рівнянням 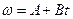, де 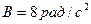. Знайти дотичну силу 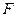, що прикладена до ободу диска. Тертям знехтувати.

3.6. По дотичній до колеса радіусом 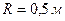і масою 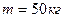прикладена сила 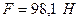. Знайти кутове прискорення 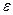колеса. Через який час 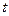після початку дії сили колесо буде мати частоту обертання 100 об/с. Колесо вважати однорідним диском. Тертям знехтувати.

3.7. На однорідний суцільний циліндричний вал радіусом 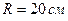, момент інерції якого 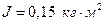, намотана невагома нитка, до кінця якої прикріплений вантаж масою 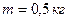. До початку обертання валу висота вантажу над підлогою становила . Визначити: 1) час опускання вантажу до підлоги; 2) силу натягу нитки; 3) кінетичну енергію вантажу в момент удару об підлогу.

3.8. На барабан радіусом 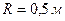намотано невагомий шнур, до кінця якого прив’язано вантаж масою 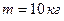. Знайти момент інерції барабана, якщо відомо, що вантаж опускається з прискоренням . Прискорення вільного падіння .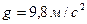

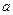3.9. На барабан масою намотано невагомий шнур, до кінця якого прив’язано вантаж масою . Знайти прискорення вантажу. Барабан вважати однорідним диском. Тертям знехтувати.

3.10. Два вантажі масами 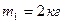та з’єднані невагомою ниткою, що перекинута через блок масою . Знайти: 1) прискорення 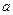, з яким рухаються вантажі; 2) силу натягу 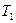та 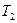нитки, до якої підвішені вантажі. Блок вважати однорідним циліндром. Тертям знехтувати. Прискорення вільного падіння .

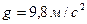3.11. Дві гирі з різними масами з’єднані невагомою ниткою, що перекинута через блок, момент інерції якого 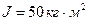. Радіус блока 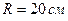. Момент сил тертя блока, що обертається . Знайти різницю сил натягу нитки 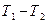по обидві сторони блока, якщо відомо, що блок обертається з кутовим прискоренням . Блок вважати однорідним диском.

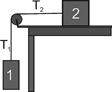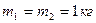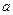3.12. Блок масою закріплено на кінці стола (див. рис. 3.1.) Вантажі 1 та 2 однакової маси з’єднані ниткою, що перекинута через блок. Коефіцієнт тертя вантажу 2 по поверхні столу . Знайти прискорення , з яким рухаються вантажі та сили натягу нитки 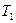і 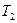. Тертям у блоці знехтувати. Рис. 3.1

3.13. Однорідний стрижень масою 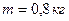підвішений горизонтально за кінці на двох нитках. Знайти силу натягу однієї з ниток одразу після спалювання другої нитки. Прискорення вільного падіння .

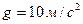3.14. Маховик радіусом і масою 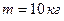з’єднаний з двигуном за допомогою привідного паса. Сила натягу паса, що рухається без проковзування становить . Яку частоту обертання 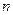буде мати маховик через час 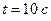після початку руху ? Маховик вважати однорідним диском. Тертям знехтувати.

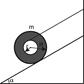
3.15. На важкий барабан, що обертається навколо горизонтальної осі, намотаний тонкий невагомий шнур. По шнуру вгору лізе мавпочка масою 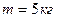. Визначити її прискорення відносно шнура, якщо її швидкість відносно землі постійна. Момент інерції барабана 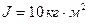, а його радіус 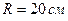. Прискорення вільного падіння .

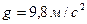3.16. З похилої площини, яка складає кут з горизонтом, скочується без ковзання куля. Визначити час руху кулі по похилій площині, якщо відомо, що її центр мас при скочуванні понизився на . Тертям знехтувати. Прискорення вільного падіння .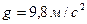

3.17. Знайти відносну похибку 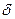, яка отримується при обчисленні кінетичної енергії кулі, що котиться, якщо не враховувати її обертання.

3.18. Котушка з ниткою знаходиться на похилій площині (рис. 3.2.) Рис. 3.2

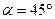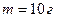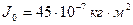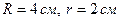з кутом нахилу . Вільний кінець нитки прикріплено до стіни так, що нитка паралельна до похилої площини. Визначити прискорення, з яким котушка рухається по похилій площині. Маса котушки . Момент інерції котушки відносно її осі симетрії . Коефіцієнт тертя котушки по площині . Радіуси котушки . Прискорення вільного падіння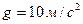

3.19. Куля масою котиться без ковзання, вдаряється об стіну і відскакує від неї. Швидкість кулі до удару в стіну 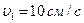, після удару 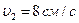. Знайти кількість теплоти 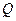, що виділилась при ударі об стіну.

3.20. Диск масою котиться без ковзання по горизонтальній поверхні з швидкістю 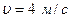. Знайти кінетичну енергію диска.

3.21. Обруч та диск однакової маси котяться без проковзування з однаковою швидкістю. Кінетична енергія обруча . Знайти кінетичну енергію диска .

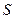3.22. Хлопчик котить обруч по горизонтальній дорозі із швидкістю . На яку віддаль може закотитись обруч на похилу площину за рахунок кінетичної енергії, якщо зміна висоти площини дорівнює 1 м на 10 м довжини площини. Прискорення вільного падіння .

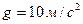3.23. Мідна куля радіусом обертається з частотою 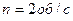навколо осі, що проходить через її центр. Яку роботу 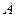необхідно виконати, щоб збільшити кутову швидкість кулі 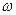вдвічі? Густина міді .

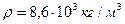3.24. Знайти лінійні прискорення 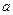центрів мас кулі, диска та обруча, які скочуються без проковзування з похилої площини. Кут нахилу площини . Початкові швидкості тіл дорівнюють нулю. Порівняти знайдені прискорення з прискореннями тіл, що ковзають по похилій площині без тертя. Прискорення вільного падіння .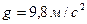

3.25. Колесо, обертаючись рівносповільнено, зменшило за час 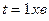частоту обертання від до 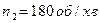. Момент інерції колеса 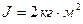. Знайти кутове прискорення 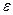колеса, момент сил гальмування 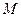, роботу 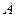сил гальмування та число обертів 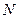, які здійснило колесо за час .

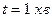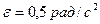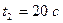3.26. Махове колесо починає обертатись з кутовим прискоренням і через час після початку руху набуває момент імпульсу . Знайти кінетичну енергію колеса через час після початку руху.

3.27. Однорідний стрижень довжиною 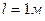підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. На який кут 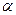необхідно відхилити стрижень, щоб його нижній кінець при проходженні положення рівноваги мав швидкість 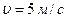? Прискорення вільного падіння .

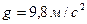3.28. Однорідний стрижень довжиною 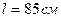підвішений на горизонтальній осі, що проходить через верхній кінець стрижня. Яку швидкість 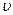необхідно надати нижньому кінцю стрижня, щоб він зробив повний оберт навколо осі ? Прискорення вільного падіння .

3.29. Олівець довжиною 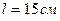, поставлений вертикально, падає на стіл. Яку кутову швидкість 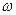та лінійну швидкість 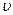будуть мати в кінці падіння середина та верхній кінець олівця ? Прискорення вільного падіння .

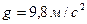3.30. Горизонтальна платформа масою 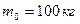обертається навколо вертикальної осі, що проходить через центр платформи з частотою . Людина, масою 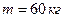, стоїть при цьому на краю платформи. З якою частотою 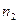почне обертатись платформа, якщо людина перейде від краю платформи в її центр? Вважати платформу однорідним диском, а людину – точковою масою.

3.31. Яку роботу 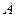здійснює людина, переміщаючись з краю платформи в її центр в умовах, викладених в задачі 3.30? Радіус платформи .

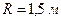3.32. Дерев’яний стрижень масою 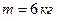і довжиною може обертатись у вертикальній площині відносно осі, що проходить через верхній кінець стрижня. В нижній кінець стрижня потрапляє куля масою , що летіла із швидкістю 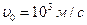, напрямленою перпендикулярно до осі стрижня, і застрягає в ньому. Визначити: 1) кінетичну енергію стрижня після удару; 2) кут, на який стрижень відхилився від вертикалі.

3.33. На ідеально гладкій горизонтальній поверхні лежить стрижень довжиною 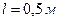і масою 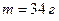. В одну з точок стрижня вдаряє кулька масою 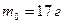, яка рухається по поверхні перпендикулярно до стрижня. Вважаючи удар абсолютно пружним, визначити на якій віддалі 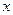від середини стрижня повинен відбутися удар, щоб кулька передала стрижню всю свою кінетичну енергію?

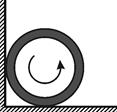3.34. Знайти максимальний гіроскопічний тиск осі турбіни, встановленої на кораблі. Корабель зазнає кільової качки з амплітудою 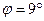і періодом навколо напрямку, перпендикулярного до осі ротора. Ротор турбіни масою 3500 кг і радіусом 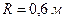обертається з частотою 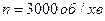. Віддаль між підшипниками . Рис. 3.3

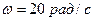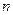3.35. Тонкостінний циліндр радіусом розкрутили до кутової швидкості і поставили в куток, як показано на рис. 3.3. Коефіцієнт тертя між циліндром і стінками . Скільки обертів зробить циліндр до повної зупинки?

3.36. Маховик обертається з частотою 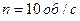. Його кінетична енергія 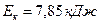. За який час момент сил 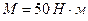, прикладений до маховика, збільшить кутову швидкість 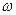маховика вдвічі?

3.37. Однорідний стрижень довжиною 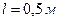здійснює малі коливання у вертикальній площині навколо горизонтальної осі, що проходить через його верхній кінець. Знайти період коливань 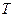стрижня.

3.38. Однорідний диск радіусом 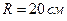коливається навколо горизонтальної осі, що проходить на віддалі від центра диска. Визначити період 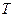коливань диска відносно цієї осі.

3.39. На кінцях вертикального стрижня закріплено два вантажі. Центр мас вантажів знаходиться нижче середини стрижня на віддалі 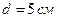. Знайти довжину стрижня 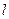, якщо відомо, що період малих коливань стрижня з вантажами навколо горизонтальної осі, що проходить через його середину, . Масою стрижня знехтувати.

3.40. До середини однорідного стрижня довжиною і масою , верхній кінець якого підвішено на шарнірі, прикріплено горизонтально пружина з жорсткістю (див. рис. 3.4.). В положенні рівноваги пружина не деформується. Знайти період

Рис. 3.4 малих коливань стрижня в площині, що проходить через

стрижень і пружину.