Количество информации при неполной достоверности и статистической зависимости сообщений

Определим количество информации, передаваемое сообщениями через их энтропии.

Если перед передачей энтропия сообщений равна H(x) и передача осуществляется без искажений, то после передачи неопределенность полностью устраняется, т.е. становится равной нулю. Следовательно, количество информации при передаче можно определить, используя выражение

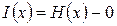. (2.17)

Оно числено равно исходной энтропии сообщений.

Если же при передаче возможны искажения, то передавая сообщения Х мы получим сообщения Y, в которых будет некоторое количество неопределенности. Таким образом, перед началом передачи энтропия сообщений будет Н(х), а после передачи Н(х/y). Следовательно, количество информации можно определить с помощью выражения

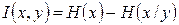. (2.18)

Используя выражения (2.10), (2.11), можно так же записать

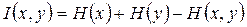, (2.19)

следовательно,

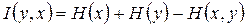и (2.20)

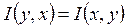, (2.21)

т.е. количество информации, которое содержится в сообщении Y относительно сообщения Х, равно количеству информации, которое содержится в сообщении Х относительно сообщения Y. Поэтому 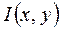и 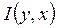называют полной взаимной информацией.

Используя (2.4) , (2.9) , (2.19), можно записать

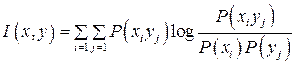. (2.22)

Аналогично получим выражение для непрерывных X и Y

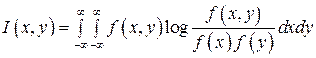. (2.23)

В отличие от энтропии количество информации для непрерывных сообщений не зависит от масштаба, если масштабы Х и Y одинаковы.

Полная статистическая независимость X и Y имеет место при высоком уровне помех, когда сигнал полностью подавляется. В этом случае 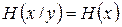и, следовательно, ,

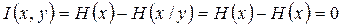т.е. информация не передается.

Избыточность сообщений

Сообщение может состоять из отдельных элементов (слов, букв, цифр и т.п.), каждый из которых можно рассматривать как сообщение более низкого ранга. В этом случае сообщение следует рассматривать как сложное, и его энтропия определяется энтропией элементов, их вероятностными характеристиками и статистическими свойствами (степенью зависимости).

Сообщение, в котором элементы некоррелированы (статистически не зависимы) и равновероятны, обладает максимальной энтропией (2.12) , (2.15) H_max (x) . В противном случае энтропия сообщения уменьшается. Сообщения, энтропия которых максимальна, являются оптимальными с точки зрения наибольшего количества передаваемой информации. Мерой количественной оценки того, насколько данное реальное сообщение по своей энтропии отличается от соответствующего ему оптимального сообщения: является коэффициент сжатия

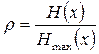. (2.24)

Если передается последовательность сообщений, то справедливо равенство

,

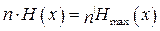где n и n^ç длина последовательностей реальных и оптимальных сообщений. Тогда коэффициент сжатия можно выразить через длины последовательностей

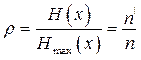. (2.25)

Таким образом, реальные сообщения при одинаковой информативности обладают определенной избыточностью (длиннее) по сравнению с оптимальными. Мерой избыточности является коэффициент избыточности

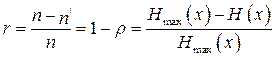(2.26)

Избыточность приводит к увеличению времени передачи сообщений, излишней загрузке каналов связи. Однако избыточность повышает помехоустойчивость сообщений. Все языки обладают избыточностью, что позволяет восстановить слова и даже целые фразы при наличии ошибок.

Наконец, сообщения могут формироваться источником с большим или меньшим темпом.

В этой связи вводится еще одна характеристика - производительность источника, которая характеризуется величиной энтропии, формируемой источником в единицу времени

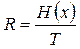, (2.27)

где H(x) - величина энтропии, формируемой источником за время Т.

Контрольные вопросы

1.Дать определение информации.

2.Отличие энтропии от информации.

3.Свойства энтропии.

4.Определение количества информации при неполной достоверности сообщений.

5.Что характеризует избыточность сообщений?

6.Чем определяется коэффициент сжатия информации?