Уравнение Шредингера. Волновая функция

В начале XX века противоречие целого ряда экспериментов существующей теории привели к созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

Дифракционная картина наблюдаемая для микрочастиц, характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям. В одних направлениях наблюдается большее число частиц, чем в других. Т.е. в одних направлениях появление частиц более вероятно, чем в других. Для описания вероятности dW нахождения частицы в данном элементе объема dV вводят Y-функцию, которую называют амплитудой вероятности или волновой функцией 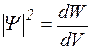. Волновая функция имеет следующий статистический (вероятностный) смысл: квадрат модуля волновой функции определяет вероятность нахождения частицы в момент времени t в области с координатами x и x+dx, y и y+dy, z и z+dz.

Уравнение, описывающее движение микрочастицы в различных силовых полях, называется волновым уравнением. Такое уравнение сформулировано Э.Шредингером. Для стационарных состояний, т.е. состояний с фиксированным состоянием энергии, для одномерного случая уравнение Шредингера имеет вид

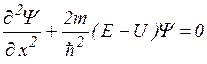, (3.7.1)

Вероятность W обнаружения частицы в области от x₁ до x₂ имеет вид

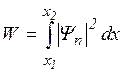(3.7.2)

Y_n– нормированная волновая функция, соответствующая данному состоянию.

Поскольку вероятность того что заданная частица находится в предоставленной ей объеме равна единице то условие нормировки вероятности примет вид

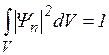(3.7.3)

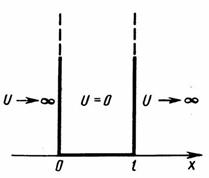Рассмотрим качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси Ох)

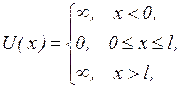(3.7.4)

где l — ширина «ямы», а энергия отсчитывается от ее Рис. 3.11

дна.

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

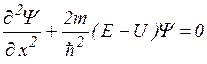, (3.7.5)

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = 1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

Y(0) = Y(l) = 0.

В пределах «ямы» (0 £ х £ l) уравнение Шредингера сведется к уравнению

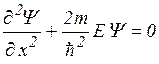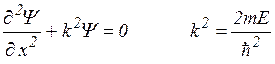или (3.7.6)

Общее решение данного дифференциального уравнения:

Y(х) = А sin kx + B cos kx.

Так как Y (0) = 0, то В = 0. Тогда

Y (x) = A sin kx. (3.7.7)

Условие Y(l) = А sin kl = 0 выполняется только при kl = pn, где n — целые числа, т.е. необходимо, чтобы

k = p n/l

Из решения следует, что

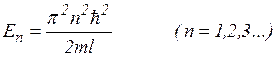(3.7.8)

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях E_n зависящих от целого числа n. Следовательно, энергия E_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии E_n называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным квантовым числом.

Подставив в решение значение k, найдем собственные функции:

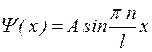(3.7.9)

Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде

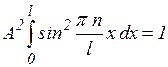
В результате интегрирования получим 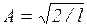, а собственные функции будут иметь вид

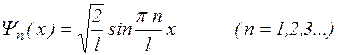(3.7.10)

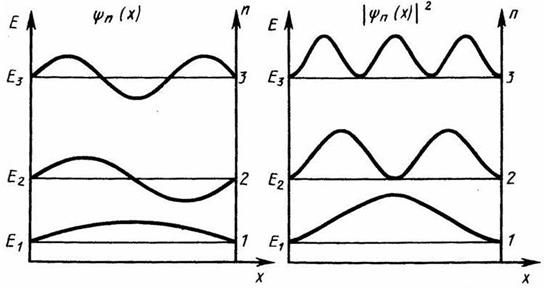
Графики собственных функций Y_n(x), соответствующие уровням энергии при n=1,2,3, приведены на рис. 3.12а. На рис. 3.12б, изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная 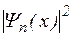для n =1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n = 2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.

a b

Рис. 3.12

3.8. Атом водорода в квантовой механике

Решение задачи об энергетических уровнях электрона для атома водорода сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

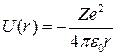(3.8.1)

где r — расстояние между электроном и ядром.

Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера, учитывающему значение (3.8.1):

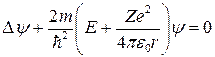(3.8.2)

где т — масса электрона, Е — полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (3.8.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важней­ших результатов, которые из него следуют, пояснив их физический смысл.

1. Энергия. В теории дифференциальных уравнений доказывается, что уравнения типа (3.8.2) имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции y, только при собственных значениях энергии

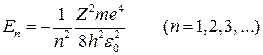(3.8.3)

т. е. для дискретного набора отрицательных значений энергии.

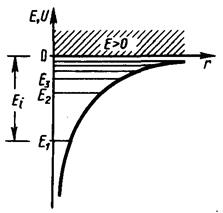
Таким образом,как и в случае «потенциальной ямы» с бесконечно высокими «стенками» и гармонического осциллятора решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е₁, E₂, Е₃,... показаны на рис. 3.13 в виде горизонтальных прямых. Самый нижний уровень Е₁, отвечающий минимальной возможной энер­гии, —основной, все остальные (Е_n >Е₁, n = 2, 3, ...) —возбужденные. Рис. 3.13

При Е<0 движение электрона являетсясвязанным — он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = ¥ E_¥ = 0. При Е > 0 движение электрона являетсясвободным; область непрерывного спектра Е > 0 (заштрихована на рис. 3.13) соответствуетионизованному атому. Энергия ионизации атома водорода равна

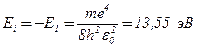
Выражение (3.8.3) совпадает с формулой, полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следстви­ем самой теории, вытекают непосредственно из решения уравнения Шредингера.

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (3.8.2) удовлетворяют собственные функции 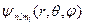, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным т_l.

Главное квантовое число n, согласно (3.8.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с еди­ницы:

n=1,2,3, …

Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

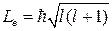(3.8.4)

где l — орбитальное квантовое число, которое при заданном n принимает значения

l = 0,1, …, (n - 1), (3.8.5)

т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L_l момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_ez на направление z внешнего магнитного поля принимает квантованные значения, кратные ћ:

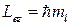(3.8.6)

где т_l — магнитное квантовое число, которое при заданном l может принимать значения

m = 0, ± 1, ± 2, …, ± l, (3.8.7)

т. е. всего 2l+1 значений. Таким образом,магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации.

Наличие квантового числа m_l должно привести в магнитном поле к расщеплению уровня с главным квантовым числом п на 2l+1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщеп­ление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландс­ким физиком П. Зееманом (1865—1945) и получило названиеэффекта Зеемана. Расщеп­ление уровней энергии во внешнем электрическом поле, тоже доказанное эксперимен­тально, называетсяэффектом Штарка

Хотя энергия электрона и зависит только от главного квантового числа п, но каждому собственному значению Е_n (кроме Е₁) соответствует несколько собственных функций 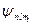, отличающихся значениями l и m_l. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном п орбитальное квантовое число l может изменяться от 0 до п–1 (см. (3.8.5)), а каждому значению l соответствует 2l+1 различных значений m_l (3.8.7), то число различных состояний, соответствующих данному п, равно

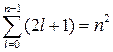(3.8.8)

Так как при движении электрона в атоме существенны волновые свойства электрона, то квантовая механика вообще отказывается от клас­сического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема. Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в раз­личных точках объема атома. Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число m_l характеризует ориентацию электронного облака в пространстве.

Состояние электрона, харак­теризующееся квантовыми числами l=0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l=1 — p-состоянием, l=2 — d-состоянием, l=3 — f-состоянием и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n=2 и l=0 и 1 обозначаются соответственно символами 2s и 2р.

Спектр. Квантовые числа n, l и m_l позволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора (см. рис. 3.14).

В квантовой механике вводятсяправила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света.

1) изменение орбитального квантового числа Dl удовлетворяет условию

Δl = ± 1 (3.8.9а)

2) изменение магнитного квантового числа Dm_l удовлетворяет условию

Δm =0, ± 1 (3.8.9б)

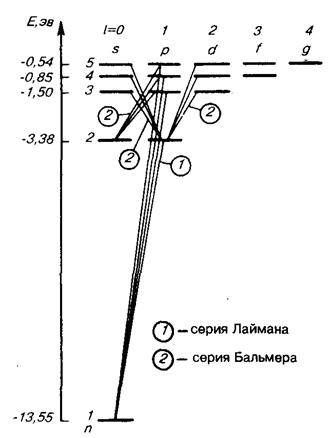
Учитывая число возможных состояний, соответствующих данному n, и правило отбора (3.8.9), рассмотрим спектральные линии Рис. 3.14

атома водорода (рис.3.14 ):

серии Лаймана соответствуют переходы np → 1s (n=2, 3, …);

серии Бальмера — np →2s, ns → 2p, nd → 2p (n=3, 4, …); и т. д.

3.9. Принцип неразличимости тождественных частиц.

Фермионы и бозоны

Если перейти от рассмотрения движения одной микрочастицы (одного электрона) к многоэлектронным системам, то проявляются особые свойства, не имеющие аналога в классической физике. Пусть квантово-механическая система состоит из одинаковых частиц, например электронов. Все электроны имеют одинаковые физические свойства — массу, электрический заряд, спин и другие внутренние характеристики (например, квантовые числа). Такие частицы называют тождественными.

Необычные свойства системы одинаковых тождественных частиц проявляются в фундаментальном принципе квантовой механики — принципе неразличимости тож­дественных частиц, согласно которому невозможно экспериментально различить тож­дественные частицы.

В классической механике даже одинаковые частицы можно различить по положе­нию в пространстве и импульсам. Если частицы в какой-то момент времени пронуме­ровать, то в следующие моменты времени можно проследить за траекторией любой из них. Классические частицы, таким образом, обладают индивидуальностью, поэтому классическая механика систем из одинаковых частиц принципиально не отличается от классической механики систем из различных частиц.

В квантовой механике положение иное. Из соотношения неопределенностей вытека­ет, что для микрочастиц вообще неприменимо понятие траектории; состояние микроча­стицы описывается волновой функцией, позволяющей вычислять лишь вероятность (|y|²) нахождения микрочастицы в окрестностях той или иной точки пространства. Если же волновые функции двух тождественных частиц в пространстве перекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно лишь говорить о вероятности нахождения в данной области одной из тождест­венных частиц. Таким образом, в квантовой механике тождественные частицы полно­стью теряют свою индивидуальность и становятся неразличимыми. Следует подчерк­нуть, что принцип неразличимости тождественных частиц не является просто следстви­ем вероятностной интерпретации волновой функции, а вводится в квантовую механику как новый принцип, который, как уже указывалось, является фундаментальным.

Принимая во внимание физический смысл величины |y|², принцип неразличимости тождественных частиц можно записать в виде

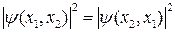(3.9.1)

где x₁ и х₂ — соответственно совокупность пространственных и спиновых координат первой и второй частиц. Из выражения (3.9.1) вытекает, что возможны два случая:

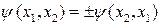(3.9.2)

т. е. принцип неразличимости тождественных частиц ведет к определенному свойству симметрии волновой функции. Если при перемене частиц местами волновая функция не меняет знака, то она называется cимметричной, если меняет — антисимметричной. Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса. Частицы с полуцелым спином (например, электроны, протоны, нейтроны) описываются ан­тисимметричными волновыми функциями и подчиняются статистике Ферми — Дира­ка; эти частицы называютсяфермионами. Частицы с нулевым или целочисленным спином (например, p-мезоны, фотоны) описываются симметричными волновыми функ­циями и подчиняются статистике Бозе — Эйнштейна; эти частицы называются бозонами. Сложные частицы (например, атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спив — полуцелый), а из четно­го — бозонами (суммарный спин целый).

Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули (1900—1958), что явилось еще одним доказательством того, что спин является фун­даментальной характеристикой микрочастиц.

3.10. Принцип Паули.

Распределение электронов в атоме по состояниям

Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:

главного n (n = 1, 2, 3, …),

орбитального l (l = 0, 1, 2, …, n-1)

магнитного m_l (m_l = -l, …, -1, 0, + 1,, …, +l)

магнитного спинового m_s (m_s = +1/2, -1/2)

Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел п, l, m_l и т_s т. е.

Z(n, l, m_l , m_s ) = 0 или 1, (3.10.1)

где Z(п, l, m_l, т_s) — число электронов, находящихся в квантовом состоянии, описыва­емом набором четырех квантовых чисел: п, l, m_l, т_s. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно формуле, данному n соответствует n² различных состояний, от­личающихся значениями l и m_l. Квантовое число т_s может принимать лишь два значения (± ½). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

(3.10.2)

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются поподоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n–1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке опреде­ляется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l+1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 3.1.

Главное квантовое число n

Символ оболочки

K

L

M

N

O

Максимальное число электронов в оболочке

Орбитальное квантовое число l

Символ подоболочки

1s

2s

2p

3s

3p

3d

4s

4p

4d

4f

5s

5p

5d

5f

5g

Максимальное число электронов в подоболочке

Таблица 3.1

Принцип Паули, лежащий в основе систематики заполнения электронных состояний в атомах, позволяет объяснитьПериодическую систему элементов Д. И. Менделеева (1869) —фундаментального закона природы, являющегося основой современной химии, атомной и ядерной физики.

Так как химические и некоторые физические свойства элементов объясняются внешними (валентными) электронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах. Поэтому для объяснения таблицы будем считать, что каждый последующий элемент образован из предыдущего прибавлением к ядру одного прото­на и соответственно прибавлением одного электрона в электронной оболочке атома. Взаимодействием электронов пренебрегаем, внося, где это необходимо, соответст­вующие поправки. Рассмотрим атомы химических элементов, находящиеся в основном состоянии.

Единственный электрон атома водорода находится в состоянии 1s, характеризу­емом квантовыми числами п=1 , l=0, m_l=0 и m_s=± ½; (ориентация его спина произвольна). Оба электрона атома Не находятся в состоянии 1s, но с антипараллельной ориентацией спина. Электронная конфигурация для атома Не записывается как 1s²(два 1s-электрона). На атоме Не заканчивается заполнение K-оболочки, что соответствует завершению I периода Периодической системы элементов Менделеева (табл. 3.2).

Пери- од

Z

Эле- мент

K

L

M

Пери- од

Z

Эле- мент

K

L

M

N

1s

2s

2p

3s

3p

1s

2s

2p

3s

3p

3d

4s

4p

I

H

IVa

K

-

He

Ca

-

II

Li

Sc

Be

Ti

B

V

C

Cr

N

Mn

O

Fe

F

Co

Ne

Ni

III

Na

IVb

Cu

Mg

Zn

Al

Ga

Si

Ge

P

As

S

Se

Cl

Br

Ar

Kr

Таблица 3.2

Таким образом, открытая Менделеевым периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов. Так, инертные газы имеют одинаковые внешние оболочки из 8 электронов (заполненные s- и p-состояния); во внешней оболочке щелочных металлов (Li, Na, К, Rb, Cs, Fr) имеется лишь один s-электрон; во внешней оболочке щелочноземельных металлов (Be, Mg, Ca, Sr, Ba, Ra) имеется два s-электрона; галоиды (F, О, Br, I, At) имеют внешние оболочки, в которых недостает одного электрона до оболочки инертного газа, и т. д.

3.11. Спонтанное и вынужденное излучения

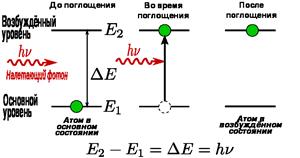
Как отмечалось выше, атомы могут находиться лишь в квантовых состояниях с дискрет­ными значениями энергии Е₁, Е₂, Е₃, ... Ради простоты рассмотрим только два из этих состояний (1 и 2) с энергиями Е₁ и Е₂. Если атом находится в основном состоянии 1, то под действием внешнего излучения может осуществиться вынужденный переход в воз­бужденное состояние 2 (рис. 3.15а), приводящий к поглощению излучения. Вероят­ность подобных переходов пропорциональна плотности излучения, вызывающего эти переходы.

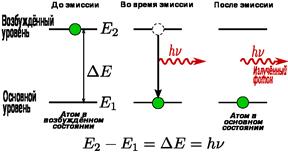
Атом, находясь в возбужденном состоянии 2, может через некоторый промежуток времени спонтанно, без каких-либо внешних воздействий, перейти в состояние с низшей энергией (в нашем случае в основное), отдавая избыточную энергию в виде электромаг­нитного излучения (испуская фотон с энергией hn=E₂–Е₁). Процесс испускания фотона возбужденным атомом (возбужденной микросистемой) без каких-либо внешних воз­действий называется спонтанным (или самопроизвольным) излучением (рис. 3.15б). Чем больше вероятность спонтанных переходов, тем меньше среднее время жизни атома в возбужденном состоянии. Так как спонтанные переходы взаимно не связаны, то спонтанное излучение некогерентно.

a b

Рис. 3.15

В 1916 г. А. Эйнштейн для объяснения наблюдавшегося на опыте термодинамичес­кого равновесия между веществом и испускаемым и поглощаемым им излучением постулировал, что помимо поглощения и спонтанного излучения должен существовать третий, качественно иной тип взаимодействия. Если на атом, находящийся в возбуж­денном состоянии 2, действует внешнее излучение с частотой, удовлетворяющей усло­вию hv=E₂–E₁, то возникаетвынужденный (индуцированный) переход в основное состояние 1 с излучением фотона той же энергии hv=E₂–E₁ (рис. 3.16). При подобном переходе происходит излучение атомом фотона, дополнительно к тому фотону, под действием которого произошел переход. Возникающее в результате таких переходов излучение называетсявынужденным (индуцированным) излучением. Таким образом, в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызыва­ющий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Существенно, что вторичные фотоны неотличимы от первичных, являясь точной их копией.

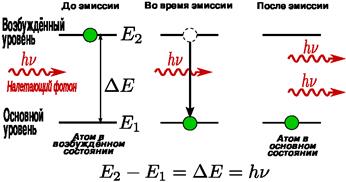
Рис. 3.16

Эйнштейн и Дирак показали, что вынужденное излучение (вторичные фотоны) тождественно вынуждающему излучению (первичным фотонам): оно имеет такие же частоту, фазу, поляризацию и направление распространения, как и вынуждающее излучение. Следовательно, вынужденное излучение строго когерентно с вынуждающим излучением, т. е. испущенный фотон неотличим от фотона, падающего на атом.

Испущенные фотоны, двигаясь в одном направлении и встречая другие возбужден­ные атомы, стимулируют дальнейшие индуцированные переходы, и число фотонов растет лавинообразно. Однако наряду с вынужденным излучением возможен и кон­курирующий процесс — поглощение. В системе атомов, находящейся в термодинамическом равновесии, поглощение падающего излучения будет преобладать над вынужденным, т. е. падающее излучение при прохождении через вещество будет ослабляться.

Чтобы среда усиливала падающее на нее излучение, необходимо создать неравновесное состояние системы, при котором число атомов в возбужденных состояниях было бы больше, чем их число в основном состоянии. Такие состояния называются состояниями с инверсией населенностей. Процесс создания неравновесного состояния вещества (перевод системы в состояние с инверсией населенностей) называется накачкой. Накачку можно осуществить оптическими, электрическими и другими способами.

3.12. Оптические квантовые генераторы (лазеры)

Практически инверсное состояние среды осуществлено в принципиально новых источ­никах излучения —оптических квантовых генераторах, илилазерах (от первых букв английского названия Light Amplification by Stimulated Emission of Radiation — усиление света с помощью вынужденного излучения). Важнейшими из существующих типов лазеров являютсятвердотельные, газовые, полупроводниковыеижидкостные (в основу такого деления положен тип активной среды). Лазер обязательно имеет три основных компонента (рис 3.17):

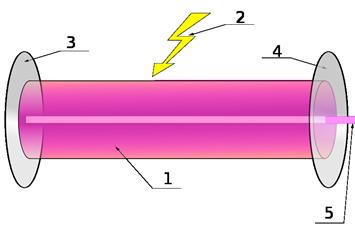1) активную среду, в которой создаются состояния с инверсией населенностей;

2) систему накачки (устройство для создания инверсии в активной среде);

3) оптический резонатор (устройство, выделя­ющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).

Рис. 3.17

1 — активная среда; 2 — энергия накачки лазера;

3 — непрозрачное зеркало; 4 — полупрозрачное зеркало; 5 — лазерный луч.

Первым твердотельным лазером (1960; США), работающим в видимой области спектра (длина волны излучения 0,6943 мкм), был рубиновый лазер. В нем инверсная населенность уровней осуществляется по трехуровневой схеме, предложенной в 1955 г. Н. Г. Басовым и А. М. Прохоровым. Кристалл рубина представляет собой оксид алюминия Аl₂О₃, в кристаллической решетке которого некоторые из атомов Аl замещены трехвалентными ионами Cr³⁺ (0,03 и 0,05% ионов хрома соответственно для розового и красного рубина). Для оптической накачки используется импульсная газоразрядная лампа.

При интенсивном облучении рубина светом мощной импульсной лампы атомы хрома переходят с нижнего уровня 0 на уровни широкой полосы 2 (рис. 3.18а). Так как время жизни атомов хрома в возбужден­ных состояниях мало (меньше 10^–7 с), то осуществляются либо спонтанные переходы 2®0 (они незначительны), либо наиболее вероятные безызлучательные переходы на уровень 1 (он называется метастабильным) с передачей избытка энергии решетке кристалла рубина. Переход 1®0 запрещен правилами отбора, поэтому длительность возбужденного состояния 1 атомов хрома порядка 10^–3 с, т. е. примерно на четыре порядка больше, чем для состояния 2. Это приводит к «накоплению» электронов на уровне 1.

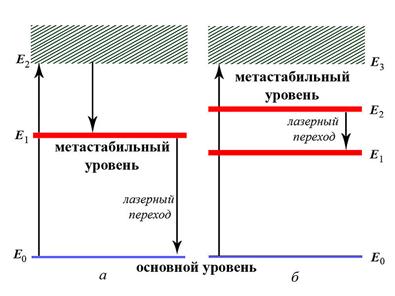
Рис. 3.18

В гелий-неоновом лазере реализуется, так называемая, четырехуровневая схема (рис 3.18б): гелий служит носителем энергии возбуждения, а неон дает лазерное излучение. Электроны, образующиеся в разряде, при столкновениях возбуждают атомы гелия, которые переходят в возбуж­денное состояние 3s. При столкновениях возбужденных атомов гелия с атома­ми неона происходит их возбуждение и они переходят на один из верхних уровней неона, который расположен вблизи соответствующего уровня гелия. Переход атома неона с верхнего уровня 3s на один из нижних уровней 2p приводит к лазерному излучению с l=632,8 нм. (рис 3.19)

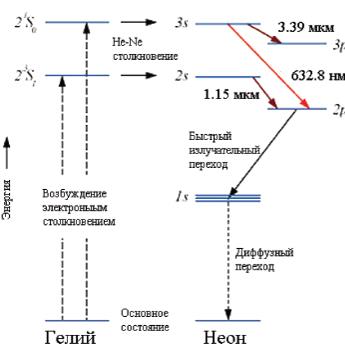
Рис 3.19

Для выделения направления лазерной генерации используется принципиально важ­ный элемент лазера —оптический резонатор. В простейшем случае им служит пара обращенных друг к другу параллельных зеркал на общей оптической оси, между которыми помещается активная среда. Как правило, зеркала изготовляются так, что от одного из них излучение полностью отражается, а второе — полупрозрачно. Фотоны, движущиеся под углами к оси кри­сталла или кюветы, выходят из активной среды через ее боковую поверхность. Те же из фотонов, которые движутся вдоль оси, многократно отразятся от противоположных торцов, каждый раз вызывая вынужденное испускание вторичных фотонов. Многократно усиленный поток фотонов выходит через полупрозрачное зеркало, создавая строго направленный световой пучок огромной яркости. Таким образом, оптический резонатор «выясняет» направление (вдоль оси) усиливаемого фотонного потока.

Лазерное излучение обладает следующими свойствами:

1. Временная и пространственная когерентность. Время когерентности составляет 10^–3 с, что соответствует длине когерентности порядка 10⁵ м (l_ког = сt_ког), т. е. на семь порядков выше, чем для обычных источников света.

2. Строгая монохроматичность (Dl<10^–11 м).

3. Большая плотность потока энергии. Если, например, рубиновый стержень при накачке получил энергию W=20 Дж и высветился за 10^–3 с, то поток излучения Ф_е=20/10^–3 Дж/с=2×10⁴ Вт. Фокусируя это излучение на площади 1 мм², получим плотность потока энергии Ф_е/S = 2×10⁴/10^–6 Вт/м² = 2×10¹⁰ Вт/м².

4. Очень малое угловое расхождение в пучке. Например, при использовании специ­альной фокусировки луч лазера, направленный с Земли, дал бы на поверхности Луны световое пятно диаметром примерно 3 км (луч прожектора осветил бы поверхность диаметром примерно 40 000 км).

У большинства лазеров к.п.д. составляет 0,1—1%. СО₂-лазер непрерывного действия, генериру­ющий инфракрасное излучение (l=10,6 мкм), к.п.д. которого (30%) превосходит к.п.д. существующих лазеров, работающих при комнатной температуре.

Необычные свойства лазерного излучения находят в настоящее время широкое применение. Лазеры применяются для обработки, резания и микросварки твердых материалов. Лазеры применяются для скоростного и точного обнаружения дефектов в изделиях, для тончайших операций (например, луч СО₂-лазера в качестве бескровного хирургического ножа), для исследования механизма химических реакций и влияния на их ход, для получения сверхчистых веществ. Применения лазеров в настоящее время столь обширны, что даже их перечисление в объеме настоящего курса просто невозможно.

Очень перспективны полупроводниковые лазеры, так как они облада­ют широким рабочим диапазоном (0,4—30 мкм) и возможностью плавной перестрой­ки частоты их излучения. Их важнейшее преимущество состоит в большом быстродействии и высоком к.п.д., превышающем 70%. Именно это определяет применение полупроводниковых лазеров в системах оптоволоконной связи, устройствах записи и считывания информации с комакт-дисков. Полупроводниковые лазеры определили появление в офисах высокопроизводительной копировальной техники.