Условия наблюдения интерференции

Рассмотрим несколько характерных случаев:

1. Ортогональность поляризаций волн.

При этом 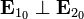и . И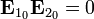нтерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.

2. В случае равенства частот волн 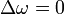и контраст полос не зависит от времени экспозиции .

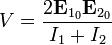3. В случае значение функции 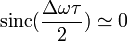и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0

4. В случае 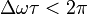контраст полос существенным образом зависит от разности частот и времени экспозиции.

В физике когерентностью называется скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени и при сложении колебаний получается колебание той же частоты.

Классический пример двух когерентных колебаний — это два синусоидальных колебания одинаковой частоты.Опыт Юнга — эксперимент, проведённый Томасом Юнгом и ставший экспериментальным доказательством волновой теории света. Результаты эксперимента были опубликованы в 1803 году.

В опыте пучок света направляется на непрозрачный экран-ширму с двумя параллельными прорезями, позади которого устанавливается проекционный экран. Этот опыт демонстрирует интерференцию света, что является доказательством волновой теории. Особенность прорезей в том, что их ширина приблизительно равна длине волны излучаемого света. Ниже рассматривается влияние ширины прорезей на интерференцию.

Если исходить из того, что свет состоит из частиц (корпускулярная теория света), то на проекционном экране можно было бы увидеть только две параллельных полосы света, прошедших через прорези ширмы. Между ними проекционный экран оставался бы практически неосвещенным.

С другой стороны, если предположить, что свет представляет собой распространяющиеся волны (волновая теория света), то, согласно принципу Гюйгенса, каждая прорезь является источником вторичных волн.

Если вторичные волны достигнут линии в середине проекционного экрана, находящейся на равном удалении от прорезей, синхроннои в одной фазе, то на серединной линии экрана их амплитуды прибавятся, что создаст максимум яркости. То есть, максимум яркости окажется там, где согласно корпускулярной теории, яркость должна быть практически нулевой. Корпускулярная теория света является неверной, когда прорези достаточно тонкие, создавая тем самым интерференцию.

На определенном удалении от центральной линии, напротив, волны окажутся в противофазе — их амплитуды компенсируются, что создаст минимум яркости (темная полоса). По мере дальнейшего удаления от средней линии яркость периодически изменяется, возрастая до максимума и снова убывая.

На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.

Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника.

1. Метод Юнга. Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников.

2. Зеркала Френеля. Свет от источника S падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180°. Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S₁ и S₂ лежат на одной и той же окружности радиуса r с центром в О.

3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.

Подставив найденное значение в условия, получим, что максимумы интенсивности будут наблюдаться в случае, если а минимумы — в случае, если Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно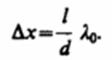

6. Интерференция в тонких плёнках. Полосы равной толщины и равного наклона

Интерференция света в тонких плёнках

Интерференция в тонкой плёнке. Альфа — угол падения, бета — угол отражения, жёлтый луч отстанет от оранжевого, они сводятся глазом в один и интерферируют.

Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга^[1]. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной 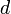, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при , где — длина волны. Если нм, то толщина плёнки равняется 550:4=137,5 нм.

Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности хода лучей, для двух лучей

— условие максимума;

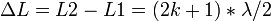— условие минимума,

где k=0,1,2... и — оптическая длина пути первого и второго луча, соответственно.

Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльяхбабочек, в цветах побежалости, и т. д.

Дифракция света

Дифракция — совокупность явлений, которые объясняются волновой природой света, и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью. И-ия и д-ия заключаются в перераспределении световой энергии и получении max и min. Но инт-ия при конечном числе источников. Для наблюдения д-ии надо создать спец условия. Два вида дисперсии: 1)Френеля или дисперсия в сходящихся лучах 2)Фраунгофера или в параллельных лучах.

Принцип Гюйгенса — Френеля: каждая т. фронта волны является источником новых вторичных волн. Новое положение фронта волны представляет собой поверхность огибающую вторичные волны. Вторичные волны сферические и при расчете амплитуды световых колебаний в какой либо т. находящейся на каком-то расстоянии можно заменить эквивалентной ему системе вторичных источников малых участков. Фазы всех вторичных источников строго согласованы и они все когерентны и когерентны основному источнику. Каждый источник вторичных волн служит источником света и сферической волны. Ее амплитуда dE=KA₀dScos(ωt-kx+φ)/r — математическая запись принципа Гюйгенса. Результат колебаний это суперпозиция по всей поверхности. E=∫(S)(k(φ)(A₀cos(ωt-kx+φ)/r))dS. Если часть поверхности занята экраном, то вторичные волны не излучают.

Метод зон Френеля.Согласно Френеля амплитуда световых колебаний в определенной т. можно рассчитать используя метод: Наблюдатель в т. М. Фронт разбивают на зоны. Одна зона от другой находится на λ/2. Зоны 1, 2, 3 — зоны Френеля. Если четные , то светлые. Колебания приходящие в т. М от 2-х соседних зон находятся в противофазе и результирующая фаза колебания отличается на π. Результирующая амплитуда А=А₁-А₂+А₃ Это выражение можно записать так: А=А₁/2+(А₁/2-А₂+А₃/2)+(А₃/2-А₄+А₅/2)+… А=А₁/2. Вычислим площадь зон: ΔS_m=S_m-S_m-1, r_m²=a²-(a-h_m)²=(b-mλ/2)²-(b+h_m)², h_m=(bmλ+m²λ²/4)/2(a+b). При λ→0 h_m=bmλ/2(a+b), S=2πRh, S_m=2πah_m=πabmλ/(a+b), ΔS=πλab/(a+b). Площадь зон Френеля постоянна. Амплитуда колебаний в т. М зонами Френеля образуют монотонно убывающую последовательность А₁>А₂>А₃… Радиус n-ой зоны определяется так: r_m=√(abmλ/(a+b)). Основные параметры: высота зоны h_m, радиус зоны r_m, площадь S_m. Т.о. амплитуда создаваемая в т. М всей поверхностью = половине амплитуды создаваемой в центре.

Д-ия на круглом отверстии. Без преграды А=А₁/2 и т.о. отверстие которое открывает не > число зон приводит к >> амплитуды в 2 раза, а интенсивности в 4. Д-ая картина от круглого отверстия имеет вид чередующихся светлых и светлых концентрических колец. В центре либо светлое, либо темное пятно. Если падает белый, то кольца имеют радужную окраску. Если щель открывает > число зон, то чередование наблюдается в очень маленькой области.

Дифракция Фраунгофера

Пусть на щель шириной b нормально падает плоская монохроматическая волна. Все точки волновой поверхности, открытые щелью, являются источниками вторичных волн, которые когерентны и распространяются по всем направлениям. Поставим между щелью и экраном наблюдения линзу, которая собирает параллельные лучи в одну точку. Дифракция в параллельных лучах называется дифракцией Фраунгофера. В результате интерференции вторичных волн на экране получится дифракционная картина.

В центре дифракционной картины будет светлая полоса - центральный максимум, так как при φ = 0 все волны придут на экран в точку М₀ в одинаковой фазе и усилят друг друга. Чтобы определить результат интерференции вторичных волн при φ ≠ 0, разобьем открытый участок волновой поверхности на ряд зон Френеля. В данном случае они будут представлять собой узкие полоски, параллельные краям щели.

При четном числе зон Френеля m₁= 2k будет наблюдаться минимум интенсивности, при нечетном m₁= 2k +1 - максимум. Условие дифракционного минимума для одной щели имеет вид

где k = 1, 2, 3, ...

"Плюс-минус" показывает, что картина симметрична относительно центрального максимума.

Условие дифракционного максимума от щели имеет следующий вид k называется порядком максимума или минимума, k = 1, 2, 3

Дифракционная решетка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность.