Интерференция в тонких пленках

Рассмотрим прозрачную однородную пластинку толщиной d. Пусть на нее от точечного источника падает пучок параллельных лучей (Рис.1.26).

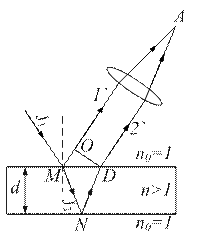
Рис. 1.26

Падающий луч частично отразится от верхней поверхности пластинки в точке М, частично, пройдя через пластинку, отразится от ее нижней поверхности в точке N. Таким образом, из одного луча получается два когерентных I^′ и 2^′. Если эти лучи свести в точку А, то они интерферируют и в зависимости от разности хода Δ дают максимум или минимум. Определим разность хода Δ лучей I^′ и 2^′. Для этого покажем фронт отраженных лучей ОD.

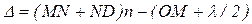
Учет λ/2 здесь связан с тем, что при отражении луча I^′ в точке М от оптически более плотной среды (n>n₀) происходит изменение фазы его колебаний на противоположную (Δφ=π), что равносильно дополнительной разности хода на λ/2. Выражая отрезки: МN, ND и ОМ через толщину d пластинки, получим:

;

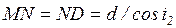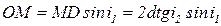
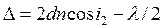или 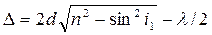(1.50)

Если Δ равна четному числу полуволн 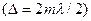, то будет наблюдаться максимум в точке А, если 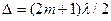-минимум. Величина m определяет порядок интерференционного максимума (или минимума).

Как следует из (1.50), при неизменных n, d, λ каждому значению угла падения лучей i₁ (наклону) в интерференционной картине соответствует своя интерференционная полоса (полосы равного наклона).

При интерференции от пленки переменной толщины d оптическая разность хода Δ (1.50) меняется с толщиной d пленки: условия max и min соответствуют одинаковым толщинам d. В этом случае интерференционная картина образует т.н. полосы равной толщины.

В предыдущих выводах мы считали λ = const (монохроматический свет). Естественный же свет в видимом диапазоне представляет набор семи основных цветов с разными λ. В этом случае интерференционные максимумы (полосы) для разных λ оказываются смещенными, так что поверхность пластинки будет иметь радужную окраску. Такую окраску имеют, например, на поверхности воды тонкие пленки масла, мыльные пленки, крылья стрекоз, цвета побежалости на поверхности металла после нагрева и т.д.

Реально на пленках меняются как α так и угол падения i₁, поэтому наблюдаются интерференционные картины смешанного типа.

Явление интерференции в тонких пленках находит применение для определения длин волн излучения источников света, для контроля чистоты обработки полированной поверхности, коэффициента расширения тел при нагревании и т.д. Существуют специальные приборы-интерферометры, предназначенные для этих целей. Существуют также методы просветления оптики - нанесение на поверхность линз или призм оптических приборов тонких прозрачных пленок толщиной равной λ/4, чтобы отраженные от линзы лучи, проходя дважды через толщину пленки, приобретали разность хода Δ=λ/2 и гасились. Благодаря этому потери светового потока на отражение объективов будут минимальными.

Частным случаем интерференционных полос равной толщины являются кольца Ньютона. Они образуют от воздушной прослойки между поверхностями стеклянной плоскопараллельной пластинки и линзой (Рис.1.27) и представляет собой чередующиеся светлые и темные кольца (исследованы были Ньютоном). Рассмотрим их.

Рис.1.27

Луч 1 отражается в точке А от верхней границы воздушной прослойки, луч 2-в точке В от нижней границы прослойки. Лучи 1 и 2 когерентны. В связи с интерференцией интенсивность света, воспринимаемая наблюдателем, будет или максимальной или минимальной. Это зависит от оптической разности хода Δ лучей, приходящих в точку наблюдения

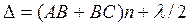
Показатель преломления для воздушной прослойки n≈1. Прибавление λ/2 к разности хода лучей в уравнении (1.50) объяснено выше. Обозначим толщину воздушной прослойки в месте отражения лучей через d и с учетом того, что АВ≈ВС≈d, запишем:

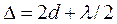(1.51)

Из рисунка 4.10 видно, что 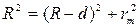, где R-радиус кривизны линзы; r_m-радиус кольца Ньютона .

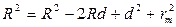Так как d мало по сравнению с R, то величиной d² можно пренебречь и считать, что 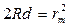, откуда

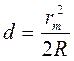
Подставляя d в формулу (1.25), получим:

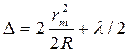(1.51)

Условие минимума света, т.е. наблюдения темного кольца Ньютона в отраженном свете, будет выполняться, если оптическая разность хода лучей будет равна нечетному числу полуволн. Приравнивая уравнения (1.44) и (1.51), получим:

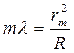(1.52)

откуда радиусы r_m темных колец Ньютона

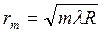(1.53)

m - номер темного кольца Ньютона.

Приравнивая (1.51) и (1.43), получим уравнение для определения радиусов светлых колец Ньютона в отраженном свете. Аналогичную картину можно наблюдать и в проходящем свете.