Термодинамические свойства чистых

РЕАЛЬНЫХ ВЕЩЕСТВ

8.1 Термическое уравнение состояния. р,u, T – поверхность

Термодинамический анализ реальных процессов, работы технических устройств по преобразованию энергии одного вида в другие требует знания теплофизических свойств веществ, обобщаемых термическим, либо калорическим уравнениями состояния. Задача определения вида термического уравнения состояния достаточно сложна и в аналитическом виде при определенных допущениях может быть решена с использованием основных положений молекулярно-кинетической теории.

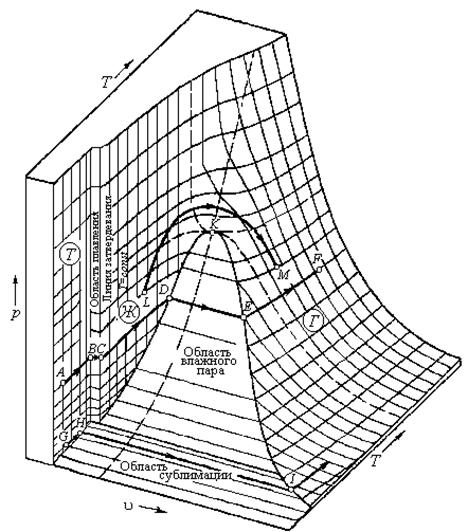
Рисунок 8.1 – р, u, T – диаграмма чистого вещества

Для простых термодинамических систем, используя Первый и Второй законы термодинамики, можно записать

.

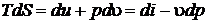Если известно термическое уравнение состояния, то используя записанное выражение, можно вычислить калорические свойства веществ.

Рассмотрим чистые вещества, для равновесных состояний каждой из фаз которых имеется определенное термическое уравнение состояния

.

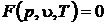Конкретный вид уравнения чаще всего определяется на основе анализа опытных данных. Записанное в неявном виде уравнение состояния термодинамической системы, состоящей из чистого вещества геометрически может быть представлено в виде пространственной поверхности состояния, в основании которой лежит u,T – плоскость, а давление 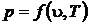играет роль третьей координаты. На поверхности обозначены области, отображающие поведение системы в каждой из трех наиболее распространенных при нормальных условиях фаз веществ – газообразной, жидкой и твердой. Кроме областей однофазного состояния системы (гомогенные области) можно отметить существование областей двухфазных-гетерогенных состояний. Такими двухфазными областями является область насыщения: область влажного пара, область плавления и область сублимации. Малым удельным объемам соответствует область твердого тела (твердой фазы вещества), в которой даже при сравнительно больших перепадах по давлению и температуре объем тела изменяется весьма незначительно. При переходе по изобаре из окружности точки А в окресность точки В наблюдается небольшое изменение объема и рост температуры, что соответствует нагреву твердой фазы вещества. В точке В температура достигает температуры плавления. В процессе плавления температура и давление остаются неизменными, то есть процесс плавления – это изобарно-изотермический процесс. В точке С плавление завершено и вещество находится в жидком состоянии. Граничная линия из точек типа “С” называется линией отвердевания. С дальнейшем нагреванием при постоянном давлении жидкость расширяется. В точке D на линии кипения происходит следующий фазовый переход при повторном изобарно-изотермическом процессе с существенным ростом объема, в процессе которого вещество переходит в паровую фазу. В точке Е выкипает вся жидкость и вещество находится в газообразной (паровой) фазе. Правую границу, на которой вещество находится в виде сухого насыщенного пара принято называть линией конденсации. Вправо от этой границы состояние вещества принято называть перегретым паром. Смесь кипящей жидкости с содержащимся в ней паром принято называть влажным паром. Если к твердому телу подводить тепло при низком давлении, то в точке Н тело достигает пограничной кривой, которую называют линией сублимации (или возгонки). В этом случае тело не плавится, а начинает испаряться. Процесс непосредственного перехода из жидкой фазы в паровую принято называть сублимацией. Обратный процесс непосредственного перехода из паровой фазы в твердую фазу принято называть десублимацией. При температуре и давлении превышающим точку К двухфазной области не существует и наблюдается непрерывный переход из жидкого в паровое состояние с непрерывным накапливанием паровых свойств. Эта область состояний вещества впервые была обнаружена Эндрюсом и правильно объяснена в 1869 г.

Линии конденсации и испарения сходятся в точке К, которую принято называть критической. Изобару и изотерму, проходящие через критическую точку, принято называть критическими: Т = Т_кр, Р = Р_кр.

Критические давление, температура и удельный объем для каждого из веществ являются характеристическими величинами. Равновесие между жидкой и газовой фазами возможно лишь при температуре и давлениях ниже критических.

8.2 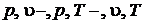– диаграммы

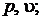
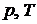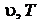Проекция р,u, T – поверхности на плоскости и представляет собой диаграммы, на которых также возможно выделить три области существования основных фаз веществ, разделяемых тремя кривыми – плавления, парообразования и сублимации (рисунок 8.2).

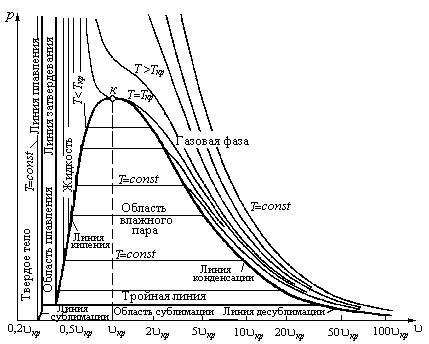
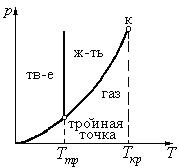
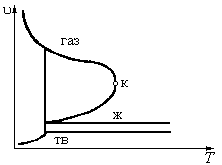
Рисунок 8.2

Возможные проекции р, u, T – диаграммы на соответствующие плоскости

В связи с тем, что отмеченные процессы относятся к числу изобарно-изотермических процессов, их проекции на р, T – диаграмме сливаются в одну линию, на которой можно отметить две характерные точк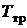и и 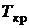. В точке 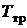сходятся все три кривые фазовых переходов, следовательно в тройной точке имеет место равновесное состояние всех трех фаз: жидкой, твердой паровой. Для воды в тройной точке 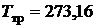К, 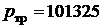Па. Кривая парообразования заканчивается в критической точке 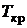, где сходятся кривые кипения и конденсации. При 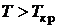четко выраженная граница между жидким и парообразным состояниями отсутствует. Это позволяет жидкости и газы объединить под общим названием – сплошная (текучая) среда, которая способна воспринимать лишь сжимающие усилия (напряжения) и не в состоянии противостоять растягивающим усилиям.

Опыты Эндрюса

Опыты показывают, что некоторые вещества при комнатной температуре, находящиеся в газообразном состоянии, можно перевести в жидкое путем повышения давления с отводом тепла. Физика этого процесса достаточно проста. В процессе изотермического сжатия растет давление газа (пара) до тех пор, пока оно не достигает давления насыщающих паров 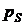, после чего начинается изобарно-изотермический процесс конденсации газа, ход которого, например, для углекислоты, представлен на рисунке 8.3.

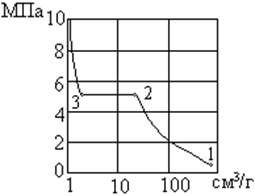
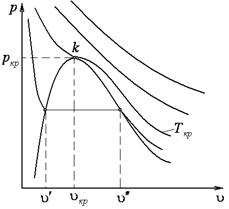
Рисунок 8.3 Изотерма фазовых переходов СО2

Рисунок 8.4 Экспериментальные изотермы Эндрюса

Проведя эксперименты для углекислоты, находящейся при различных начальных температурах, Эндрюс Томас впервые установил, что чем выше начальная температура вещества, тем меньше разница между удельными объемами паровой и жидкой фаз. Протяженность горизонтального участка процесса фазового перехода пропорциональна теплоте фазового перехода вещества (теплота парообразования или теплота конденсации). При критической температуре – горизонтальный участок стягивается в точку 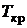, в которой исчезают различия между жидкой и паровой фазами. Критические давление и температура – максимальные значения для области возможного равновесного двухфазного состояния.

В критической точке 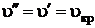. В этой точке обращается в нуль и теплота парообразования 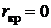, что видно из уравнения Клапейрона-Клазиуса:

.

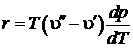В критической точке изотерма претерпевает перегиб в результате чего она имеет горизонтальную касательную, а первые и вторые производные от давления по удельному объему, взятые по температуре, в критической точке равны нулю.

, .

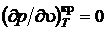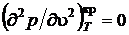Для различных веществ критические параметры в критической точке различны.

Ван-дер-Ваальсовский газ

Модель идеального газа предполагает отсутствие столкновений между молекулами, т. е. отсутствие сил межмолекулярного взаимодействия. Кроме того, допускается, что молекулы одноатомны, атомы представляют собой материаьные точки. Это в принципе означает, что газ раз выведенный из состояния равновесия, никогда не сможет в него вернуться.

Необходимо знать каким изменениям в уравнении состояния приведет учет столкновений и наличие конечного объема у молекул газа?

Если молекулы притягиваются друг к другу, то энергия газа должна быть равна сумме кинетической энергии его молекул и потенциальной энергии их взаимодействия. Реальный газ должен обладать несколько меньшим давлением, чем идеальный, находясь при одних и тех же значениях объема и температуры. Кроме того, наличие собственного объема, в отличие от точечной идеализации, приведет к уменьшению объема, в котором перемещаются молекулы в процессе теплового движения, а, следовательно, чуть меньше будут и расстояния между молекулами. Этот эффект также изменяет потенциальную энергию системы, и, как оказывается, облегчает процесс расширения газа.

Перечисленные отличительные факты приводят к тому, что поведение реального газа отклоняется от уравнения состояние. Причем величина отклонения тем больше, чем выше давление и ниже температура.

Попытки многих ученых создать универсальное для всех газов уравнение состояния потерпели неудачу. Такое уравнение может быть создано лишь для сильно разреженных газов, когда они теряют свои индивидуальные макроскопические свойства и могут служить моделью любого разреженного газа. Наиболее удачно свойства реального газа описывает уравнение, предложенное Ван-дер-Ваальсом. Оно удобно тем, что достаточно хорошо качественно описывает свойства жидкой, паровой фаз и двухфазной области. Ван-дер-Ваальс предложил в уравнение Клапейрона-Менделеева ввести две поправки, учитывающие реальные свойства чистых веществ:

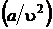– поправка, учитывающая наличие межмолекулярных сил – внутреннее давление; b – поправка, учитывающая конечный объем молекул.

Поправку b можно вычислить, допуская, что молекулы – сферы. С учетом этого предположения она оказалась равной

,

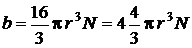где r – радиус молекулы, N – число молекул, т. е. поправка равна примерно учетверенному собственному объему всех молекул. Константа а – коэффициент пропорциональности, численное значение которого зависит от характера сил притяжения между молекулами. В настоящее время надежного способа его вычислить нет.

Уравнение Ван-дер-Ваальса

Для описания поведения реальных газов предложено большое число различных уравнений. Самым простым и хорошо описывающим качественную картину поведения веществ в жидкой и газообразной фазах является уравнение, предложенное нидерландским физиком Яном Дидериком Ван-дер-Ваальсом в 1873 г.

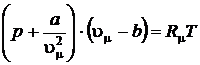, (8.1)

где р – внешнее давление, Па; a [Па×м⁶/моль], b [м³/моль].

Поправка 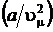по своей сути является добавкой к внешнему давлению, обусловленную взаимодействием между молекулами. Взаимное притяжение между молекулами как бы дополнительно сжимает объем.

Поправка к объему «b» как бы учитывает собственный суммарный объем молекул, недоступный для их теплового движения.

Уравнение Ван-дер-Ваальса можно записать для произвольного количества вещества в термодинамической системе

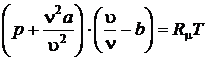, (8.2)

или умножив его на число молей n

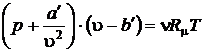, (8.3)

где , , , .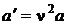

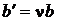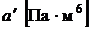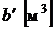Реальные газы следуют уравнению Ван-дер-Ваальса приближенно. Хотя оно и лучше чем уравнение Клапейрона-Менделеева описывает их состояние. Газ, строго подчиняющийся уравнению Ван-дер-Ваальса, принято называть Ван-дер-Ваальсовским.