Баланс энтропии для стационарного поточного процесса
Рассмотрим закрытую систему, ограниченную контрольной поверхностью, состоящую из вещества, находящегося в момент времени 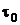 в объеме, ограниченном контрольной поверхностью, и небольшого количества вещества массой
в объеме, ограниченном контрольной поверхностью, и небольшого количества вещества массой  на входе в систему. За промежуток времени
на входе в систему. За промежуток времени  эта масса вещества поступает в контрольную поверхность и равная ей масса газа покидает контрольную поверхность. В соответствии со Вторым законом термодинамики изменение энтропии в этом процессе может быть найдено как
эта масса вещества поступает в контрольную поверхность и равная ей масса газа покидает контрольную поверхность. В соответствии со Вторым законом термодинамики изменение энтропии в этом процессе может быть найдено как
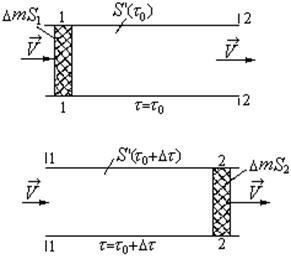 Рисунок 7.12 Баланс энтропии для стационарного поточного процесса Рисунок 7.12 Баланс энтропии для стационарного поточного процесса |
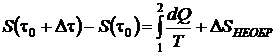 .
.
Теплота к системе не подводится и не отводится 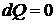 , следовательно, и
, следовательно, и
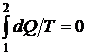 .
.
В момент времени 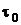 энтропия системы и вводимой массы равны
энтропия системы и вводимой массы равны
 .
.
В момент времени 
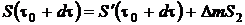 ,
,
где 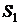 и
и 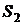 – удельные энтропии вещества во входном и выходом сечениях.
– удельные энтропии вещества во входном и выходом сечениях.
Поточный процесс стационарен, поэтому энтропия вещества в контрольной поверхности не изменяется со временем
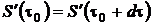 .
.
Тогда в общем случае при наличии теплообмена можно записать баланс энтропии в виде
 .
.
Если разделить его на промежуток времени  , за который протекает через контрольный объем масса
, за который протекает через контрольный объем масса  , то получим
, то получим
 ,
,
или переходя к удельным величинам, т.е. разделив на поток массы G
 .
.
Для адиабатного случая  и
и
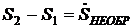 или
или  .
.
Энтропия вещества, протекающего через адиабатное контрольное пространство не может убывать, она возрастает за счет необратимости процесса при производстве энтропии.
Пример 1:
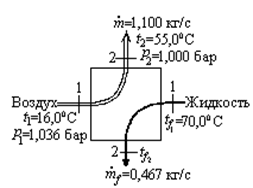 Рисунок 7.13 Рисунок 7.13 |
В адиабатном теплообменнике воздух нагревается от  °С до
°С до  °С. Массовый расход воздуха составляет
°С. Массовый расход воздуха составляет 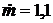 кг/с; давление воздуха в теплообменнике снижается от
кг/с; давление воздуха в теплообменнике снижается от  Па до
Па до 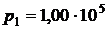 Па. Нагрев осуществляется горячей жидкостью с массовым расходом
Па. Нагрев осуществляется горячей жидкостью с массовым расходом 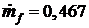 кг/с, поступающей в теплообменник при
кг/с, поступающей в теплообменник при 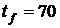 °С. Жидкость несжимаема, ее удельная теплоемкость
°С. Жидкость несжимаема, ее удельная теплоемкость 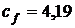 кДж/(кг×К) постоянна, изменение состояния жидкости предполагается изобарным. Изменение кинетической и потенциальной энергии пренебрежимо малы. Определить поток энтропии, произведенной в теплообменном аппарате.
кДж/(кг×К) постоянна, изменение состояния жидкости предполагается изобарным. Изменение кинетической и потенциальной энергии пренебрежимо малы. Определить поток энтропии, произведенной в теплообменном аппарате.
Поток, произведенной в нем энтропии выражается суммой изменений энтропии обоих потоков вещества.
 ;
;
 .
.
Воздух принимаем за идеальный газ с постоянной теплоемкостью 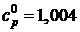 кДж/(кг×К).
кДж/(кг×К).
Энтропия воздуха в процессе теплообмена возрастает, а энтропия воды снижается.
Найдем температуру воды на выходе из теплообменного аппарата, для чего воспользуемся Первым началом термодинамики и составим баланс энергии
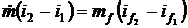 .
.
Тепло, воспринятое воздухом равно теплу отданному жидкостью.
Для воздуха запишем
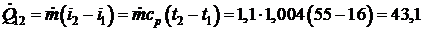 кВт;
кВт;
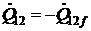 ;
;
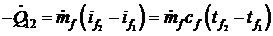 ;
;
откуда
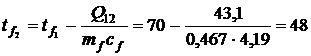 °С.
°С.
Определим произведенную в теплообменном аппарате энтропию
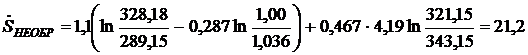 Вт/К.
Вт/К.
Этот поток энтропии порождается двумя факторами – двумя необратимыми процессами: теплообменом при конечной разности температур между потоками воздуха и вязкостной диссипацией по воздушному тракту, приводящей к снижению давления воздуха по мере его продвижения по «холодному» тракту.
Разделим полученный поток необратимой энтропии на указанные две составляющие. Для неадиабатного контрольного пространства, включающего в себя только движущийся воздух из уравнения баланса энтропии выделим энропию, произведенную в движущемся потоке:
 ,
,
учитывая, что поток тепла  , получим
, получим  .
.
После подстановки и интегрирования получим следующее выражение
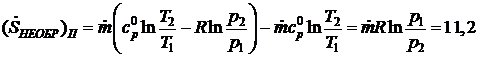 Вт/к – поток энтропии за счет вязкой диссипации.
Вт/к – поток энтропии за счет вязкой диссипации.
Пример 2:
Найти приращение энтропии в поточном процессе энергоразделения в термотрансформаторе Ранка.
Дано: Полное давление на входе –  МПа. Полная температура –
МПа. Полная температура –  К. Полное давление охлажденного потока –
К. Полное давление охлажденного потока –  МПа. Полная температура охлажденного потока –
МПа. Полная температура охлажденного потока –  К. Относительная доля охлажденного потока
К. Относительная доля охлажденного потока 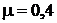 . Полное давление подогретого потока
. Полное давление подогретого потока 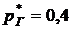 МПа. Найти приращение энтропии в системе.
МПа. Найти приращение энтропии в системе.
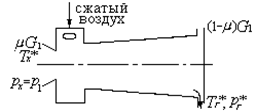

Рисунок 7.14
Приращение энтропии в системе может быть найдено по изменению энтропии в политропных процессах для охлажденной и подогретой составляющих. Из закона сохранения вещества имеем
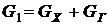 ;
;  ,
,
тогда
 ;
;  .
.
В этом случае выражение для 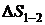 вихревой трубы в случае адиабатной оболочки примет вид
вихревой трубы в случае адиабатной оболочки примет вид
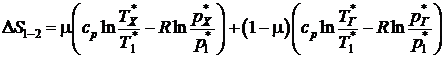 .
.
В записанном выражении нам известна температура подогретого потока  . Ее можно найти, записав закон сохранения энергии открытой адиабатной системы
. Ее можно найти, записав закон сохранения энергии открытой адиабатной системы
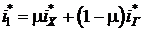 .
.
Предполагая, что изобарная теплоемкость остается неизменной, получим
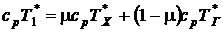 или
или  .
.
Решим последнее выражение относительно 
 К.
К.
Тогда для энтропии, подставив численное значение величин получим
 .
.
