Логарифмическая термодинамическая
Шкала температуры
Второй закон термодинамики позволяет установить температурную шкалу, не зависящую от термометрических свойств вещества. Запишем КПД цикла Карно:
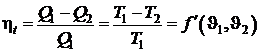 или
или
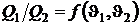 ,
,
где 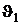 и
и 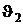 – температуры высокотемпературного и низкотемпературного источников.
– температуры высокотемпературного и низкотемпературного источников.
Пусть имеются три источника тепла с температурами 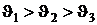 .
.
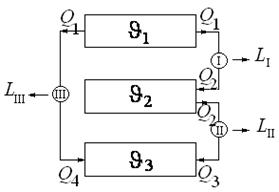 Рисунок 6.4 К выводу термодинамической шкалы температур Рисунок 6.4 К выводу термодинамической шкалы температур |
Возьмем три идеальные машины работающие по циклу Карно и осуществляющие между имеющимися источниками тепла три цикла Карно, как показано на рисунке 6.4. Составим для каждого из циклов соответствующие соотношения:
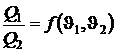 ,
, 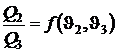 ,
, 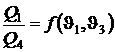 .
.
Циклы I и II образуют совокупную машину Карно, работающую в интервале температур 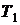 и
и 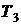 . Запишем термические КПД циклов Карно для совокупной машины I-II и машины III
. Запишем термические КПД циклов Карно для совокупной машины I-II и машины III
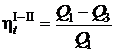 ;
; 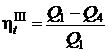 .
.
Поскольку машина III и составная машина I-II работают в одном интервале температур, то их КПД равны 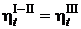 и их тепловые эффекты тоже одинаковы, следовательно,
и их тепловые эффекты тоже одинаковы, следовательно, 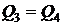 .
.
Разделим отношения теплот третьей и второй машины:
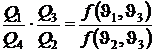 ;
; 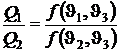 .
.
Ранее было показано, что 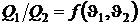 . Это возможно лишь в том случае, когда
. Это возможно лишь в том случае, когда
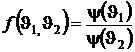 ,
,
т. е. значения функций 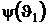 и
и 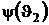 не должны зависеть от температуры Т3.
не должны зависеть от температуры Т3.
Тогда 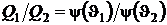
и выражение для термического КПД цикла Карно перепишется в виде
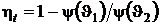 .
.
Для обратимого цикла Карно, реализуемого в бесконечно малом интервале температуры 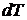 , т. е. при
, т. е. при 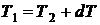 последнее выражение будет иметь вид
последнее выражение будет иметь вид
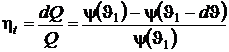 .
.
Разложим 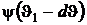 в ряд Тейлора
в ряд Тейлора
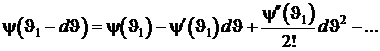 .
.
Ряд сходящийся и, ограничиваясь первыми его двумя слагаемыми, получим
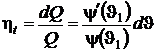 .
.
Выбор температуры 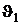 произволен, обозначая ее впредь как u, введем обозначение
произволен, обозначая ее впредь как u, введем обозначение 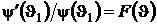 . Следовательно,
. Следовательно,
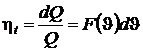 .
.
Получим дифференциальное уравнение, однозначно связывающее КПД обратимого цикла Карно с температурой J, которую называют термодинамической. Т. к. КПД цикла Карно не зависит от свойств рабочего тела, так и термодинамическая температура не будет зависеть от термических свойств вещества. Проинтегрировав, получим
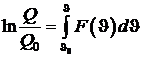 , (6.5)
, (6.5)
где 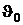 – некоторая постоянная температура,
– некоторая постоянная температура, 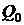 – теплота, соответствующая этой температуре.
– теплота, соответствующая этой температуре.
Из последнего выражения (6.5) следует, что можно ввести множество различных шкал термодинамической температуры, варьируя выбором типа функции 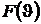 и начальной температурой
и начальной температурой 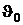 .
.
Кельвин предложил 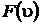 выбрать такой, чтобы температурные интервалы шкалы были пропорциональны
выбрать такой, чтобы температурные интервалы шкалы были пропорциональны 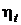 . В этом случае
. В этом случае 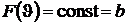 , тогда
, тогда
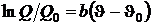 . (6.6)
. (6.6)
Пусть температурам 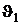 и
и 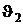 соответствуют тепловые эффекты
соответствуют тепловые эффекты 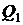 и
и 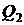 , тогда можно записать соответствующие выражения
, тогда можно записать соответствующие выражения
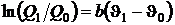 , а
, а 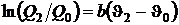 .
.
Разность температуры 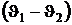 пусть будет равна известному температурному интервалу, например между температурами кипения воды и таяния льда
пусть будет равна известному температурному интервалу, например между температурами кипения воды и таяния льда
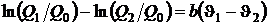 ;
; 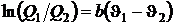 ,
,
то есть 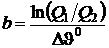 , где
, где 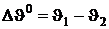 .
.
С учетом выражения для расчета константы “b”, решая (6.6) относительно температуры 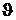 , получим
, получим
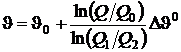 . (6.7)
. (6.7)
Таким образом, выражение (6.7), позволяет составить температурную шкалу. Такая температурная шкала получила название логарифмической. Следуя, лорду Кельвину будем считать 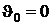 , а интервал равным 100 °С. Очевидно, что в этом случае
, а интервал равным 100 °С. Очевидно, что в этом случае 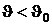 ,
, 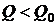 , следовательно, эта шкала предполагает наличие отрицательных температур. При
, следовательно, эта шкала предполагает наличие отрицательных температур. При 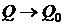 ;
; 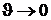 , а при
, а при 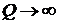 ,
, 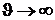 ,
, 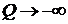 ,
, 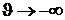 . Это означает, что в логарифмической термодинамической шкале температурный интервал равен (-¥; ¥). Однако в виду неудобства использования такая шкала температуры не получила распространения.
. Это означает, что в логарифмической термодинамической шкале температурный интервал равен (-¥; ¥). Однако в виду неудобства использования такая шкала температуры не получила распространения.
