Гоу впо рыбинская государственная авиационая
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОНАЯ
ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ ИМ. П. А. СОЛОВЬЕВА
ПИРАЛИШВИЛИ Ш. А.
ТЕРМОДИНАМИКА
ТЕРМОДИНАМИКА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
УЧЕБНОЕ ПОСОБИЕ
РЫБИНСК 2007
ОГЛАВЛЕНИЕ
| 1. Термодинамика. Основные понятия и определения | |
| 1.1 Введение в предмет и методы термодинамики | |
| 1.2 Термодинамическая система и ее состояние | |
| 1.3 Параметры состояния | |
| 1.4 Тепловое равновесие. Нулевое начало термодинамики | |
| 1.5. Термометр и эмпирическая температура | |
| 1.6 Термические и калорические параметры состояния | |
| 1.7 Термодинамический процесс | |
| 1.8 Обратимые и необратимые процессы | |
| 1.9 Стационарные поточные процессы | |
| 1.10 Круговой процесс или цикл. Прямой и обратный цикл | |
| 2. Первое начало термодинамики | |
| 2.1 Энергия системы. Внутренняя энергия | |
| 2.2 Работа в термодинамике. Работа. Механическая работа и механическая энергия | |
| 2.3 Работа изменения объема | |
| 2.4 р, u – диаграмма | |
| 2.5 Уравнение первого закона термодинамики | |
| 2.6 Энтальпия | |
| 2.7 Теплоемкость газов. Уравнение Майера | |
| 2.8 Зависимость теплоемкости от температуры | |
| 2.9 Основы молекулярно-кинетической и квантовой теории теплоемкости | |
| 2.10 Расчет газовой смеси. Способы задания газовых смесей | |
| 2.11 Термическое уравнение состояния газовой смеси | |
| 2.12 Теплоемкость смеси газов | |
| 3. Второй закон термодинамики | |
| 3.1 Энтропия и второй закон термодинамики | |
| 3.2 Применение Первого и Второго законов термодинамики к изолированным системам | |
| 3.3 Энтропия и энтальпия несжимаемой среды | |
| 3.4 T, S – диаграмма | |
| 4. Политропные процессы | |
| 4.1 Анализ политропного процесса | |
| 4.2 Частные случаи политропных процессов | |
4.2.1 Изохорный процесс 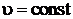 | |
4.2.2 Изобарный процесс 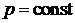 | |
4.2.3 Изотермический процесс 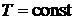 | |
4.2.4 Адиабатный процесс 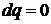 | |
| 4.3 Взаимное расположение политропных процессов в р, u –и T, S – диаграммах. С, Т – диаграмма | |
| 4.4 Экспериментальные методы определения показателя политропы | |
| 4.5 Цикл Карно. Термодинамика цикла | |
| 4.6 Теорема Карно | |
| 4.7 Логарифмическая термодинамическая шкала температуры | |
| 4.8 Шкала термодинамической температуры Кельвина | |
| 5. Второе начало и необратимость процессов преобразования энергии | |
| 5.1 Необратимость теплообмена | |
| 5.2 Перенос и производство энтропии | |
| 5.3 Диссипация энергии | |
| 5.4 Эксергия и анергия | |
| 5.5 Преобразование тепла в полезную работу | |
| 5.6 Эксергия и анергия стационарного потока | |
| 5.7 Определение потерь эксергии | |
| 5.8 Диаграмма потоков эксергии и анергии | |
| 5.9 Влияние окружающей среды на преобразование энергии | |
| 5.10 Баланс энтропии для стационарного поточного процесса | |
| 6. Термодинамические свойства чистых реальных веществ | |
| 6.1 Термическое уравнение состояния. р,u, T – поверхность | |
| 6.2 р, Т – диаграмма | |
| 6.3 Опыты Эндрюса | |
| 6.4 Ван-дер-Ваальсовский газ | |
| 6.5 Уравнение Ван-дер-Ваальса | |
| 6.6 Внутренняя энергия Ван-дер-Ваальсовского газа | |
| 6.7 Выражение критических параметров через коэффициенты a и b | |
| 6.8 Экспериментальные изотермы | |
| 6.9 Фазовые превращения | |
| 6.10 Приведенное уравнение Ван-дер-Ваальса | |
| 6.11 Термическое уравнение состояния для жидкостей и газов | |
| 6.12 Условия равновесия в гетерогенной области | |
| 6.13Свойства вещества в критическом состоянии | |
| 7 Влажный пар | |
| 7.1 Процесспарообразования | |
| 7.2 Параметры состояния в области насыщения. Правило «рычага» | |
| 7.3 Изохорный процесс. Процесс изменения состояния пара | |
| 7.4 Изобарный процесс изменения состояния водяного пара | |
| 7.5 Изотермический процесс изменения состояния водяного пара | |
| 7.6 Адиабатный процесс изменения состояния водяного пара | |
| 8 Влажный газ. | |
| 8.1 Основные понятия и определения | |
| 8.2 Экстенсивные свойства влажного воздуха | |
| 8.3 Характерные особенности изменения состояния влажного воздуха | |
| 8.4 i, d – диаграмма влажного воздуха | |
| 8.5 Основные процессы влажного воздуха | |
| 8.6 Процессы в конвективной сушилке | |
| 8.7 Примеры решения задач на влажность | |
| 9. Третье начало и элементы статической термодинамики | |
| 9.1 Третье начало термодинамики | |
| 9.2 Недостижимость абсолютного нуля | |
| 9.3 Статистическая природа второго начала термодинамики | |
| 9.4 Формула Больцмана | |
| 9.5 Статистическая формулировка второго и третьего начала | |
| 9.6 Состояние с отрицательной температурой | |
| 10. Флуктуация | |
| 10.1 Флуктуации плотности в газе | |
| 10.2 Броуновское движение | |
| 10.3 Уравнение Ланжевена | |
| 10.4 Уравнение Фоккера-Планка | |
| 11 Термодинамические потенциалы | |
| 11.1 Внутренняя энергия и уравнение Эйлера | |
| 11.2 Энтальпия как термодинамический потенциал | |
| 11.3 Функция Гельмгольца | |
| 11.4 Функция Гиббса | |
| 11.5 Порядок вычисления термодинамических параметров | |
| 11.6 Способы выравнивания частных производных через непосредственно измеренную величину |
ТЕРМОДИНАМИКА. ОСНОВНЫЕ ПОНЯТИЯ
И ОПРЕДЕЛЕНИЯ
Параметры состояния
Макроскопические величины, характеризующие физические свойства изучаемой термодинамической системы, принято называть параметрами состояния системы.
Каждому состоянию системы соответствует определенное сочетание параметров по величине, поэтому их называют функциями состояния.
Если состояние термодинамической системы не меняется со временем и свойства системы, а, следовательно, и ее термодинамические параметры, сравниваемые в различные моменты времени, одинаковы, то говорят, что система находится в состоянии равновесия.
Равновесие может быть локальным, если оно имеет место лишь в отдельных частях системы, а в других нет. Равновесие термодинамической системы обуславливается внутренними факторами и однозначно определяется совокупностью интенсивных внутренних параметров.
Параметры, выбранные в качестве определяющих состояние равновесия системы, называются независимыми. Все другие параметры могут быть выражены через эти независимые параметры. Число независимых параметров, определяющих равновесие, различно для разных систем. Они устанавливаются либо из опыта, либо теоретически исходя из молекулярно-кинетической теории строения вещества.
Для однородных термодинамических систем число независимых параметров равно двум. Это не означает обратного, т. е. что для неоднородных систем оно не может быть равным двум. В частности, любая двухфазная система в равновесном состоянии тоже однозначно определяется двумя параметрами.
Термодинамический процесс
Любая термодинамическая система, находящаяся в неравновесном состоянии обязательно через некоторое время переходит в равновесное состояние. Такие процессы изменения состояния принято называть самопроизвольными, а время перехода из неравновесного в равновесное состояние – временем релаксации.
Термодинамическая система, находясь в состоянии равновесия, выйти из него может лишь под воздействием со стороны окружающей среды. В этом случае через границы системы необходимо подвести либо отвести энергию. Всякий термодинамический процесс связан с изменением состояния термодинамической системы. Если в начале процесса система находилась в равновесном состоянии, то его изменение приводит к существенно неравновесным состояниям, когда температура и плотность по объему, занимаемому системой, становятся неодинаковыми. Таким образом, любое изменение состояния, строго говоря, протекает через неравновесные состояния. Такие процессы принято называть неравновесными либо нестатическими.
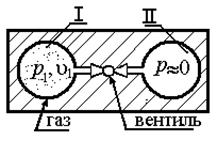 Рисунок 1.5 Процесс заполнения объема Рисунок 1.5 Процесс заполнения объема |
Рассмотрим изолированную систему, представленную на рисунке 1.5. Если открыть вентиль, то начнется процесс истечения из сосуда I и заполнение сосуда II.
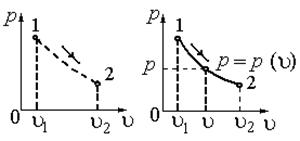 а) б) Рисунок 1.6 Представление процессов в р, u – диаграмме: а – условное изображение нестатического процесса; б – процесс квазистатического (равновесного) изменения состояния а) б) Рисунок 1.6 Представление процессов в р, u – диаграмме: а – условное изображение нестатического процесса; б – процесс квазистатического (равновесного) изменения состояния |
При этом за счет отрывных явлений в потоке газа будут возникать завихрения, создающие значительную разность давления и температуры у различных областей как втекающего потока, так и во всей области, занимаемой вторым сосудом. Переход начального равновесного состояния в конечное равновесное состояние системы будет происходить через некоторую совокупность промежуточных неравновесных состояний, описание которых уравнением состояния системы невозможно. Любое уравнение состояния справедливо лишь для равновесных состояний. Следовательно, нестатический, неравновесный процесс не может быть изображен в р,u – диаграмме.
Процессы, протекающие из начального равновесного в конечное равновесное состояние через совокупность промежуточных равновесных состояний, будем называть квазистатическими или равновесными процессами изменения состояния.
Строго говоря, равновесных или статических процессов в природе существовать не может. Для их реализации необходимо, чтобы механические или термические воздействия на систему были бесконечно малы.
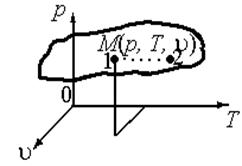 Рисунок 1.7 Термодинамическое пространство Рисунок 1.7 Термодинамическое пространство |
Таким образом, квазистатическое (квазиравновесное) состояние необходимо рассматривать как идеализированный предельный случай, когда система постоянно находится вблизи равновесных состояний, так что все ее состояние с достаточной степени точности можно описать общими для всей системы параметрами состояния.
Если соединить начальное, все промежуточные и конечное состояния линией, то на диаграмме получим кривую процесса изменения состояния, для каждой точки которой применимо термическое уравнение состояния.
Круговой процесс или цикл.
Прямой и обратный цикл
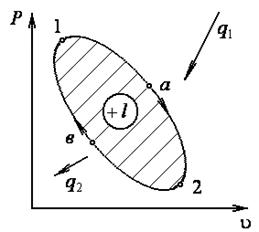 Рисунок 1.11 Цикл (круговой процесс) Рисунок 1.11 Цикл (круговой процесс) |
Если при реализации совокупности нескольких термодинамических процессов система возвращается в свое первоначальное состояние, то имеем пример кругового процесса или цикла (рисунок 1.11).
Циклом называется замкнутый круговой процесс. Если он состоит из равновесных обратимых процессов, то мы имеем случай обратимого кругового процесса, при реализации которого параметры состояния в конце цикла совпадают с их первоначальными значениями. Цикл бывает прямым и обратным. Если процессы расширения расположены над процессами сжатия, то это прямой цикл. Если наоборот, процессы сжатия расположены над процессами расширения, то это обратный цикл. По прямому циклу работают тепловые машины, по обратному холодильные установки.
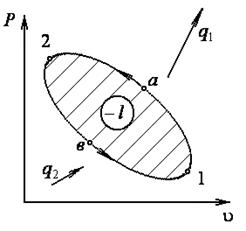 Рисунок 1.12 Обратный цикл Рисунок 1.12 Обратный цикл |
При реализации прямого цикла площадь, охваченные реализуемыми процессами численно равна работе расширения термодинамической системы. Она совершается ею над окружающей средой и поэтому имеет положительный знак 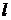 >
> 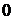 .
.
При реализации обратного цикла как видно из рисунка 1.12 процессы сжатия расположены над процессами расширения работа отрицательна. По таким циклам работают холодильные машины, тепловые насосы и некоторые устройства термостатирования. При этом для возможности реализации таких циклов необходимо работу подводить из вне. Т. е. окружающая среда совершает работу над термодинамической системой и поэтому такая работа расширения отрицательна 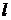 <
< 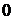 .
.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики выражает принцип сохранения энергии и приводит к определению энергоресурсов в формах, не проявляющихся в механике – внутренней энергии и теплоте. Таким образом, термодинамика расширяет круг понятий, включая в анализ такие виды энергии как химическая, электрическая, ядерная. При применении Первого закона термодинамики необходимо различать энергию, накопленную системой и энергию, переходящую границы системы при совершении процесса. Принцип сохранения энергии, в конечном счете, приводит к энергетическому балансу, связывающему изменение запаса энергии системы с энергией, переходящей в форме работы или тепла ее границы.
Накопленная системой энергия является параметром ее состояния. Этот энергетический запас представляет собой сумму кинетической, потенциальной и внутренней энергии.
Энергия, переходящая через границы системы, подразделяется на работу и теплоту, которые не являются параметрами состояния, а относятся к функциям процесса, по своей сути представляя различные формы передачи энергии.
Работа в термодинамике.
Работа изменения объема
Если силы действуют перпендикулярно границе термодинамической системы, то это может вызвать перемещение границ системы, а, следовательно, вызвать изменение ее объема.
Чаще всего это можно наблюдать в жидкостях и особенно в газах. Поршень действует на термодинамическую систему с силой (рисунок 2.2)
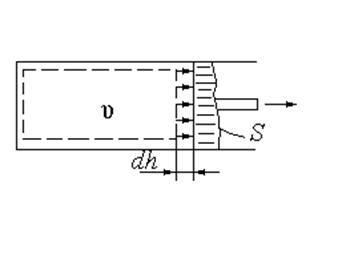 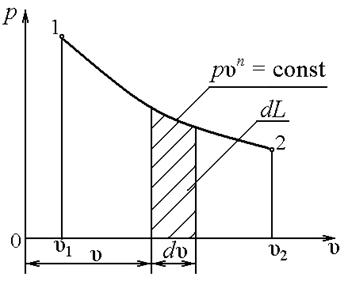 Рисунок 2.2 Рисунок 2.3 Работа расширения Работа расширения в Рисунок 2.2 Рисунок 2.3 Работа расширения Работа расширения в 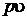 – диаграмме – диаграмме |
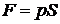 ,
,
где р – давление, Па; S – площадь поршня, м2.
При этом поршень перемещается на величину dh. В этом случае объем системы изменяется на 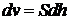 . Работа силы может быть выражена в виде
. Работа силы может быть выражена в виде 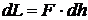 . Подставляя
. Подставляя 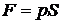 , получим
, получим
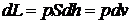 . (2.15)
. (2.15)
Для обратимых процессов вычисление конечной работы достаточно просто.
Конечная работа может быть найдена в этом случае интегрированием
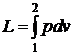 . (2.16)
. (2.16)
Интеграл берется, если известна зависимость 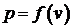 .
.
2.4 р, u – диаграмма
В термодинамике широкое распространение получила р, u – диаграмма, которую еще называют диаграммой работ. Действительно, в этой системе координат удельная работа изображается площадью под кривой процесса 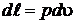 . Удельная работа при конечном изменении параметров системы может быть найдена интегралом
. Удельная работа при конечном изменении параметров системы может быть найдена интегралом
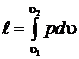 . (2.17)
. (2.17)
Проще всего этот интеграл взять для изобарного процесса. В этом случае 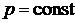 и его можно вынести за знак интеграла
и его можно вынести за знак интеграла
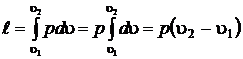 . (2.18)
. (2.18)
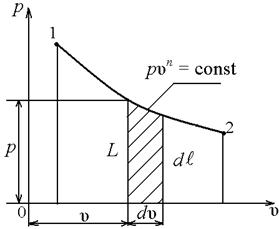 а) работа расширения а) работа расширения 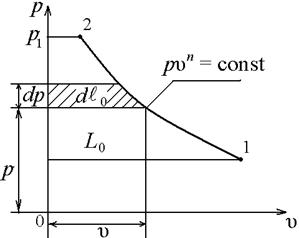 б) располагаемая работа Рисунок 2.4 б) располагаемая работа Рисунок 2.4 |
Если работа совершается термодинамической системой, то она положительна, если работа совершается над системой, то она отрицательна (рисунок 2.4, а).
При изучении термодинамики потока жидкости и лопаточных машин (компрессоров, турбин) большую роль играет располагаемая работа. В компрессоре это работа, затрачиваемая на повышения давления рабочего тела. Если при объеме uизолировать давление на dр, то элементарная работа, затраченная на сжатие составит:
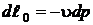 . (2.19)
. (2.19)
Для конечного процесса работа найдется как интеграл:
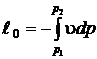 . (2.20)
. (2.20)
В р, u – диаграмме располагаемая техническая работа – 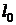 она изображается площадью между кривой процесса и осью давлений (рисунок 2.4,б).
она изображается площадью между кривой процесса и осью давлений (рисунок 2.4,б).
Энтальпия
Под энтальпией понимается тепловая функция представляющая собой полную энергию системы, состоящую из внутренней энергии u и работы затраченной на проталкивание 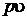 .
.
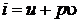 . (2.31)
. (2.31)
Энтальпия включает в себя все слагаемые, являющиеся параметрами состояния, поэтому ее дифференциал будет полным, а циркуляция от него по замкнутому контуру равна нулю.
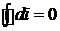 .
.
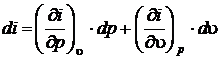
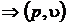
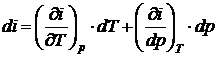
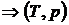 (2.32)
(2.32)
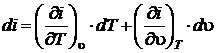
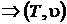
Энтальпия подчиняется закону аддитивности по сути своей являясь экстенсивным параметром 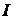 ,[Дж]. Чаще всего в расчетах используют удельную энтальпию i, [Дж/кг]
,[Дж]. Чаще всего в расчетах используют удельную энтальпию i, [Дж/кг]
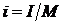 , [Дж/кг], (2.33)
, [Дж/кг], (2.33)
где М – масса вещества в системе.
Уравнение первого начала термодинамики может быть записано через энтальпию и располагаемую работу. Запишем выражение для полного дифференциала энтальпии
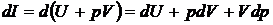 .
.
Первое начало термодинамики имеет вид
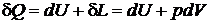
Из выражения для дифференциала энтальпии выразим сумму 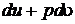
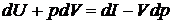
Тогда после подстановки получим
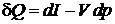 (2.34)
(2.34)
или для 1 кг вещества в системе
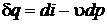 (2.35)
(2.35)
Подведенная теплота расходуется на изменение энтальпии системы и на совершение располагаемой (технической) работы.
Теплоемкость газов
Одним из проявлений взаимодействия термодинамической системы с окружающей средой является изменение температуры термодинамической системы (исключение – изотермический процесс). Обмен теплом между системой и средой оценивается экстенсивным параметром состояния – теплоемкостью, истоки которого идут еще от теплорода.
Под теплоемкостью понимают количество теплоты, которое необходимо подвести (отвести) к термодинамической системе по какому-либо процессу с тем, чтобы изменить ее температуру на 1 Кельвин.
Теплоемкость конкретного вещества зависит от его физических свойств, агрегатного состояния в котором оно находится, от температуры и в некоторой степени от давления.
В газообразном состоянии основное влияние на теплоемкость веществ оказывает температура. В этом случае разумно ввести в рассмотрение среднюю и истинную теплоемкости, понимая под последней теплоемкость при данной конкретной температуре.
Под средней теплоемкостью в интервале температур 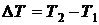 понимается отношение:
понимается отношение:
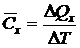 , [Дж/К] (2.36)
, [Дж/К] (2.36)
где 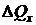 – количество теплоты, полученное телом в процессе изменения ее температуры на величину
– количество теплоты, полученное телом в процессе изменения ее температуры на величину 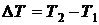 . Индекс “x” указывает на характер процесса подвода теплоты.
. Индекс “x” указывает на характер процесса подвода теплоты.
Под истиной теплоемкостью будем понимать предел отношения
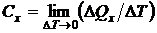 ;
; 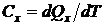 , [Дж/К] (2.37)
, [Дж/К] (2.37)
Теплоемкость системы является экстенсивным параметром. Интенсивные свойства отражают удельные теплоемкости, т. е. теплоемкости отнесенные к единице измерения количества вещества.
Массовая теплоемкость:
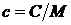 . [Дж/кг×К] (2.38)
. [Дж/кг×К] (2.38)
Объемная теплоемкость
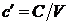 . [Дж/м3×К] (2.39)
. [Дж/м3×К] (2.39)
Мольная теплоемкость
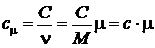 . [Дж/моль×К] (2.40)
. [Дж/моль×К] (2.40)
Между объемной и мольной теплоемкостями существует, очевидная взаимосвязь:
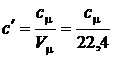 . [Дж/м3×К] (2.41)
. [Дж/м3×К] (2.41)
Аналогично можно записать зависимость, связывающую объемную и удельную (массовую) теплоемкости
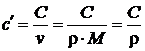 или
или 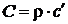
Таким образом, справедливы соотношения:
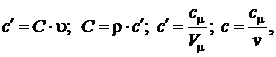
где 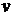 – количество вещества (число молей)
– количество вещества (число молей) 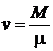 .
.
Мольная теплоемкость удобна при использовании, т. к. она зависит от особенностей структуры отдельных молекул. Введение ее дает возможность сравнить теплоемкости разных газов, ибо в 1 моле любого вещества при нормальных условиях содержится одно и тоже число молекул: 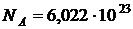 .
.
Теплота Q – есть функция процесса, а число всевозможных процессов бесчисленно велико, следовательно, и теплоемкость тела может изменяться неограниченно от 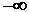 до
до 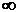 .
.
Наиболее часто используются изохорная 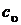 и изобарная
и изобарная 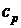 теплоемкости. Причем изобарная теплоемкость всегда больше изохорной ср > сu на величину тепла, затраченного на совершение работы расширения в изобарном процессе при изменении температуры на 1 К. Рассмотрим систему, содержащую 1 кг вещества.
теплоемкости. Причем изобарная теплоемкость всегда больше изохорной ср > сu на величину тепла, затраченного на совершение работы расширения в изобарном процессе при изменении температуры на 1 К. Рассмотрим систему, содержащую 1 кг вещества.
В соответствии с первым началом термодинамики для изохорного процесса 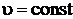 ,
, 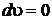 , следовательно
, следовательно
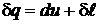
или иначе 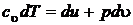 , т. к.
, т. к. 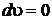 , то
, то 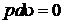 и
и
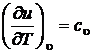 или
или 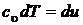 . (2.42)
. (2.42)
Для изобарного процесса, используя параметр состояния энтальпии, можно также записать 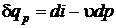 ,
, 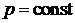 ,
, 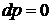 , следовательно,
, следовательно, 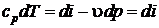
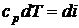 ,
, 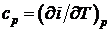 . (2.43)
. (2.43)
Уравнение Майера
Найдем зависимость между изобарной и изохорной теплоемкостями.
Воспользуемся первым началом термодинамики
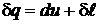 .
.
Для параметра состояния u, считая независимыми переменными u и T, можно записать выражение полного дифференциала в виде
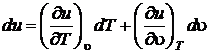 . (2.44)
. (2.44)
Подставим du в первое начало термодинамики
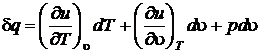 или
или
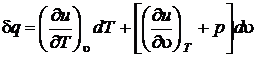 или
или
с учетом того, что 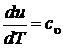 , получим
, получим 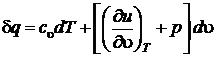 .
.
Предполагая процесс подвода тепла изобарным, после деления на dT получим
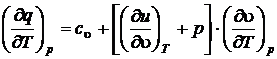 ;
; 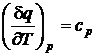 .
.
Величину 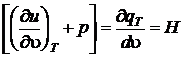 принято называть теплотой расширения – количество теплоты необходимое для изотермического увеличения объема тела на единицу объема.
принято называть теплотой расширения – количество теплоты необходимое для изотермического увеличения объема тела на единицу объема.
Тогда 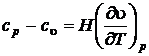 . (2.45)
. (2.45)
Для твердых и жидких фаз, слабо расширяющихся при нагревании, теплота расширения Н невелика. Мало и изменение объема 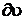 .
.
В этом случае 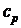 практически не отличается от
практически не отличается от 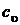
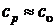 .
.
Для идеальных газов 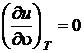 . В этом случае уравнение первого начала сводится к виду
. В этом случае уравнение первого начала сводится к виду
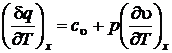 .
.
Если процесс изобарный 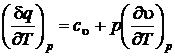 .
.
Продифференцируем уравнение состояния идеального газа при 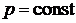
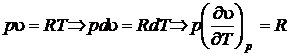 ,
,
тогда после подстановки, получим
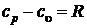 ,
, 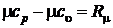 . (2.46)
. (2.46)
где 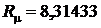 – универсальная газовая постоянная, Дж/моль×К;
– универсальная газовая постоянная, Дж/моль×К; 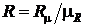 – индивидуальная газовая постоянная, Дж/кг×К. Индивидуальная газовая постоянная
– индивидуальная газовая постоянная, Дж/кг×К. Индивидуальная газовая постоянная 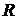 практически всегда используется в технических расчетах и в какой то степени она характеризует свойства конкретного газа.
практически всегда используется в технических расчетах и в какой то степени она характеризует свойства конкретного газа.
Теории теплоемкости
Основной предпосылкой кинетической теории газов является установленный Максвеллом и Больцманом закон о равномерном распределении энергии по степеням свободы поступательного и вращательного движений молекул газа. Из молекулярно-кинетической теории известно, что у одноатомного газа молекула имеет i = 3 степени свободы поступательного движения, у двухатомной молекулы газа к трем степеням свободы поступательного движения добавляются еще две степени свободы вращательного движения и их общее число равно 5. У трехатомных молекул и многоатомных вращательных степеней свободы 6. Для идеального газа (совершенного газа – газа подчиняющегося уравнению Клапейрона-Менделеева) внутренняя энергия однозначно определяется температурой и рассчитывается по зависимости, полученной из анализа основного уравнения молекулярно-кинетической теории. Запишем выражение для расчета внутренней энергии одного моля идеального газа:
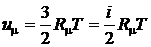 . (2.53)
. (2.53)
где 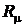 = 8,3142 [Дж/моль×К] – универсальная газовая постоянная; i – число степеней свободы. Тогда после постановки численного значения универсальной газовой постоянной для идеального газа получим
= 8,3142 [Дж/моль×К] – универсальная газовая постоянная; i – число степеней свободы. Тогда после постановки численного значения универсальной газовой постоянной для идеального газа получим
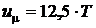 .
.
Продифференцируем внутреннюю энергию по температуре при постоянном объеме, считая, что 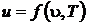
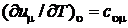 ;
; 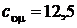 Дж/моль×К.
Дж/моль×К.
Очевидно, что на каждую степень свободы молекулы приходится одна треть от рассчитанной выше
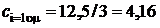 Дж/моль×К.
Дж/моль×К.
Теперь можно рассчитать теплоемкости двухатомных, трех и многоатомных газов, считая их совершенными, т. е. подчиняющимися уравнению Клапейрона-Менделеева.
Для двухатомного газа 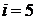 , а
, а 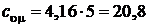 Дж/(моль×К);
Дж/(моль×К);
Для трехатомного газа 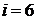 , а
, а 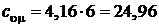 Дж/(моль×К);
Дж/(моль×К);
Однако при сравнительно высоких температурах экспериментально полученные значения теплоемкостей заметно отличаются от рассчитанных на основе положений МКТ. Это связано с тем, что в приведенной модели не учитывалась энергия, приходящаяся на степени свободы внутримолекулярного и внутриатомного движений, а также энергия, связанная с взаимодействием молекул, зависящая от изменения объема при изменении температуры. Попытка учета этих составляющих связана с тем, что атомы в молекуле не всегда жестко связаны друг с другом и могут совершать колебания друг относительно друга. Тогда для определения конфигурации молекулы требуется ввести еще одну координату. Это координата – расстояние между молекулами. Таким образом двухатомная молекула будет обладать 6-ю степенями свободы: 3 – поступательные, 2 – вращательные и 1 – колебательная степень свободы.
Если молекула состоит из n атомов, нежестко связанных между собой, то она имеет 3n степени свободы, из которых 3 – поступательные, 3 – вращательные, а остальные колебательные. Таким образом, нелинейная молекула из n атомов имеет 3n – 6 колебательных степеней свободы, а у линейных 3n – 5.
Колебательные степени свободы возбуждаются при высоких температурах. При достаточно малых амплитудах колебания атомов можно считать гармоническими осцилляторами.
Для гармонического осциллятора средние значения потенциальной и кинетической энергии равны между собой. Если в молекуле возбуждаются гармонические колебания, то по закону равнораспределения на каждую колебательную степень свободы приходится 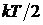 в виде кинетической и
в виде кинетической и 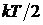 в виде потенциальной энергии. Тогда формула для подсчета числа степеней свободы будет иметь вид
в виде потенциальной энергии. Тогда формула для подсчета числа степеней свободы будет иметь вид
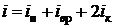 (2.45)
(2.45)
Эйнштейн, воспользовавшись квантовой теорией Планка, получил следующее выражение для мольной теплоемкости, достаточно точное для температур, применяемых в теплотехнике.
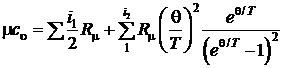 , (2.46)
, (2.46)
где 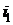 – число степеней свободы поступательного движения и вращательного;
– число степеней свободы поступательного движения и вращательного;
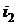 – число степеней свободы внутримолекулярных колебаний;
– число степеней свободы внутримолекулярных колебаний;
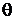 – характеристическая температура колебательного движения,
– характеристическая температура колебательного движения, 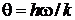
( 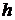 – постоянная Планка);
– постоянная Планка);
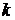 – постоянная Больцмана;
– постоянная Больцмана;
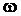 – частота колебаний в секунду;
– частота колебаний в секунду;
е – основание натуральных логарифмов;
Т – температура.
В приведенной выше формуле первый член учитывает количество теплоты, расходуемое на увеличение поступательного и вращательного движения молекул и определяется числом степеней свободы этих движений. Второй член учитывается количество теплоты, расходуемое на увеличение внутримолекулярных колебаний.
ГАЗОВЫЕ СМЕСИ
Практически во всех сферах деятельности мы сталкиваемся не с веществами в чистом виде, а с их химическими соединениями, либо с механически перемешенными веществами или растворами. К примеру, рабочие тела почти всех тепловых машин представляют собой некоторую газовую смесь. Не составляет исключение и воздух, которым мы дышим и используем в большинстве случаев как окислитель в камерах сгорания двигателей, топках различных топливосжигающих устройств. Как известно, воздух состоит из 78,08 % азота N2, 20,95 % кислорода О2, и где-то около 1 % составляют примеси других газов. С экологической точки зрения хотелось бы, чтобы процент примесей не возрастал в результате не всегда разумного вмешательства человечества в естественные массообменные процессы природы.
При термодинамических расчетах рабочих процессов тепловых машин мы сталкиваемся с необходимостью определения термодинамических параметров рабочих тел, в подавляющем большинстве случаев представляющих собой газовую смесь продуктов сгорания углеводородных топлив, что требует умения и навыков расчета газовых смесей. Следовательно, должны быть разработаны методы их расчета и способы задания газовых смесей.
3.1 Способы задания газовой смеси
Под смесью идеальных газов понимается механическая смесь химически обособленных исходных газов, подчиняющихся уравнению состояния идеального газа. Тогда будем считать, что и смесь представляет из себя некоторый самостоятельный идеальный газ, термодинамические свойства которого определяются количественным соотношением входящих в него исходных компонентов, т. е. свойства газовой смеси однозначно определяются ее составом.
Состав газовой смеси определяется количественным соотношением входящих в него компонентов и может быть задан массовыми, объемными или мольными долями.
Пусть Мсм – масса газовой смеси, а тi – масса i-го компонента, входящего в смесь. Согласно закону сохранения массы будем иметь очевидное равенство:
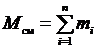 , (3.1)
, (3.1)
где n – число компонентов смеси.
Под массовой долей i-го компонента будем понимать отношение:
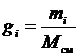 или в процентах
или в процентах 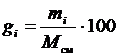 %. (3.2)
%. (3.2)
На основании закона сохранения вещества, запишем уравнение баланса массы:
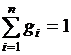 . (3.3)
. (3.3)
Если массовые доли заданы в процентах, то
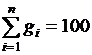 %. (3.4)
%. (3.4)
Объемные доли представляют собой отношение парциальных объемов компонентов к объему газовой смеси:
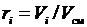 , (3.5)
, (3.5)
где Vi – парциальный объем i-го компонента; Vсм – объем газовой смеси.
Под парциальным объемом будем понимать тот объем, которым бы обладал i-й компонент, находясь при температуре 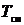 и давлении
и давлении 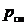 газовой смеси.
газовой смеси.
Нетрудно показать, что парциальные объемы газов прямо пропорциональны их парциальным давлениям. Парциальным называется давление, которое создавал бы i-й газ смеси, если бы он один занимал весь объем смеси, находясь в нем при температуре смеси. Запишем уравнение Бойля-Мариотта для компонента смеси:
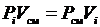 , т. е. (3.6)
, т. е. (3.6)
