Математическая модель процесса

β(Сп-С₀) = w(Cп)

Концентрация у поверхности зерна для реакции первого порядка:

Сп = C₀/(1+ k/β)

Наблюдаемая скорость превращения:

Wн = k C₀/(1+ k/β)

Влияние условий процесса (концентрации (парциального давления), температуры, скорости газового потока), режимы и лимитирующие стадии – такие же, как для процесса «сжимающаяся сфера»

Влияние условий процесса

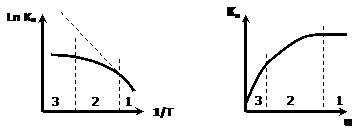Зависимость наблюдаемой константы Кн скорости превращения в гетерогенном процессе

«сжимающаяся сфера» от температуры Т и скорости обтекания частицы u режимы процесса:

1 – кинетический; 2 - переходный; 3 - диффузионный

ХП в пористом катализаторе

Принимаем, что перенос вещества из потока к поверхности катализатора достаточно интенсивен, т.е. концентрация реагентов в потоке и к поверхности одинаковы. Тогда схема процесса следующая. Исходные вещества диффундируют по «порам» катализатора внутрь пористого зерна. Одновременно происходит превращение (протекает каталитическая реакция) на стенках пор. Поскольку размер пор много меньше зерна катализатора, последнее можно представить как квазигомогенное диффузионно-проницаемое тело. Тогда диффузию в нем можно характеризовать эффективным коэффициентом диффузии D_эф , а скорость реакции относить к единице объема зерна катализатора. Предположим, что зерно катализатора – плоское тело толщиной 2R₀ с закрытыми боковыми гранями, так что диффузия протекает только в одном направление, между противоположными гранями. Процесс описывается диффузионным уравнением с источником вещества, записанным для одной половины зерна, поскольку последнее симметрично относительно плоскости симметрии, где находится начальная точка координаты R по толщине зерна:

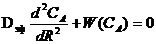
с граничными условиями

dC_A/dR=0 при R=0

C_A=C₀ при R=R₀

Пусть протекает реакция первого порядка, тогда уравнение имеет решение:

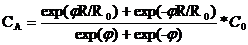
Наблюдаемую скорость превращения определим как среднеинтегральную скорость превращения в пористом зерне, отнесенную к единице объема зерна:

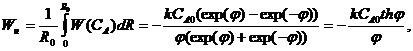здесь

thφ=( 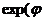) - )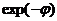/( ) 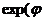+ )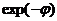, φ=R₀ 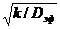- определяющий параметр (модуль Зельдовича-Тиля)

Степень использования внутренней поверхности η – отношение наблюдаемой скорости превращения, определенной при концентрации

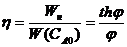
Теория химических реакторов

Химические реакторы.

Изотермические процессы в химических реакторах

Процессы протекающие при постоянной температуре, называются изотермическими процессами. При расчетах ХР, работающих в изотермическом и стационарном режиме, используются балансовые уравнения массы.

Реакторы непрерывного действия (реакторы, работающие в режиме идеального смешения и вытеснения)

РИС

Реактор непрерывного действия работает в режиме идеального смешения, если хим. состав, температура, давление и др параметры, характеризующие свойства реакционной массы, имеют одинаковые значения во всех точках реактора. Уравнение материального баланса для компонента А смеси имеет вид:

(n_A-n_A0)/v_p = W_A

Если объем реакционной смеси не меняется в результате протекающей реакции, то уравнение преобразуется к виду:

(C_A – C_A0)/τ = W_A или C_A0 *(X_A/τ) = -W_A где τ= v_p/V₀ – условное время пребывания смеси в реакторе; С_А – концентрация компонента А в смеси.

РИВ

Реакционная смесь движется в режиме идеального вытеснения, если скорости всех элементов смеси в произвольном сечении реактора равны между собой (поршневой режим), т.е. отсутствует осевое перемешивание, а радиальное перемешивание считается идеальным.

Уравнение материального баланса для модели идеального вытеснения имеет вид:

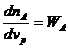, при v_p=0, n_A=n_A0

Если объемный расход реакционной смеси V – величина постоянная, тогда уравнение можно преобразовать к след выражению.

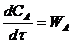, при τ = 0, С_A=С_A0

«исходная модель», в которую входят химические и физические величины и параметры – концентрация, объем реактора, величина потока, коэффициенты переноса и т.д.

«расчетная модель», в которую входят параметры в виде комбинаций первоначальных химических и физических величин. Расчетная модель получена преобразованием исходной модели и используется в программе.

Математические модели процесса в хим реакторе (простая реакция )

Режим процесса	Исходная модель	Расчетная модель
Идеальное смешение, изотермический
Идеальное вытеснение, изотермический
Идеальное смешение, неизотермический
Идеальное вытеснение, неизотермический

Математические модели процесса в хим реакторе (сложная реакция )

Режим процесса	Расчетная модель
Идеальное смешение, изотермический
Идеальное вытеснение, изотермический
Идеальное смешение, неизотермический
Идеальное вытеснение, неизотермический

ХТС представляет собой совокупность аппаратов, машин и др устройств, связанных между собой трубами, газопроводом, электротранспортом результатом которого является получение продукта. Система – совокупность элементов и связей между ними и функций как единое целое. Элемент в системе изменяет свойства входящих в него потоков. В системе можно выделить совокупность аппаратов – подсистему, например, реакторный узел. Отдельный аппарат или подсистему будем называть «расчетным элементом ХТС» или просто элементом. В элемент входят потоки («входные потоки») и выходят из него («выходные потоки»). Расчетным элементом может быть ХТС в целом.

Смеситель. Входят два потока и выходит один. В элементе происходит простое смешение потоков.

Делитель. Входит один и выходят два. Если происходит только разветвление потока, делитель называют простым, - покомпонентный составы входящих и выходящих потоков не меняются. В таких процессах, как испарение, адсорбция, ректификация, фильтрация, составы входящих и выходящих потоков различаются, и такой элемент называют делителем пропорциональным.

Реактор. Проходит один поток, но его компонентный состав принципиально меняется вследствие протекающих в элементе хим превращений.

Классификация элементов ХТС

Проводится по их назначению

- механические и гидродинамические элементы перемещают и изменяют форму и размер материала, объединяют и разделяют потоки эти операции операции осуществляются дробилками, сепараторами, насосами, фильтрами и т.д.

- теплообменные элементы изменяют температуру и теплосодержание потока, переводят вещества в другое фазовое состояние. Для этих целей служат испарители, конденсаторы, сублиматоры.

- массообменные элементы осуществляют межфазный перенос компонентов, изменение компонентного состава потоков без появления новых веществ. Эти операции проводят в дистиллятах, абсорберах, адсорберах, ректификационных колоннах, кристаллизаторах и т.д.

- реакционные элементы реализуют химические превращения кардинально изменяется состав потоков и материала. Эти процессы проходят в реакторах.

- энергетические элементы осуществляют преобразование энергии и получение энергоносителей. К ним относятся турбины, генераторы, привод для выработки механической энергии и др.