Криволинейное движение мат. точки
Криволинейное движение мат. точки
В зависимости от формы траектории различают прямолинейное движение, движение по окружности и криволинейное движение. Криволинейное движение – это движение по криволинейной траектории.При криволинейном движении вектор ускорения описывает изменение величины и направления скорости.
Ускорение – это величина, определяемая формулой w=dv/dt.
Тангенциальное ускорение –вектор,характеризующий изменение скорости по времени,направленный по касательной к траектории,численно равный 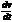
 Нормальное ускорение-вектор,характеризующий изменение скорости по направлению и направленный по разиусу к центру криволин.траектории.Численно равен
Нормальное ускорение-вектор,характеризующий изменение скорости по направлению и направленный по разиусу к центру криволин.траектории.Численно равен 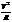
Предел отношения 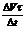 при
при 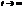 называется тангенциальным(касательным ускорением).
называется тангенциальным(касательным ускорением).
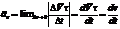
Предел отношения 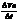 при
при 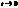 называется нормальным(центростремительным ускорением).
называется нормальным(центростремительным ускорением).
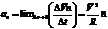 или
или 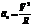
где R-радиус кривизны траектории.
Т.К. ускорения взаимно перпендикулярны:
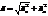
3.Движение точки по окружности.Угловое перемещение,скорость,ускорение.Связь между линейными и угловыми характеристиками.
 1)Вращательное движение-движение тела вокруг неподвижной оси,при котором все точки тела движутся по окружности,центры которых лежат на одной прямой-ось вращения
1)Вращательное движение-движение тела вокруг неподвижной оси,при котором все точки тела движутся по окружности,центры которых лежат на одной прямой-ось вращения
Угловая скорость
Угловая скорость –векторная
величина W, характеризующая
быстроту вращения твердого тела
и направленная по правилу
правого винта.
W=lim dФ/dt при dtà0, где Ф- угол поворота, t-время. Единица измерения (рад/с). Вращение с постоянной угловой скоростью называется равномерным. Если вращение является равномерным, тоW=Ф/t, где Ф- конечный угол поворота за время t.
Угловое ускорение
Угловое ускорение - векторная величина Е, Характеризующая быстроту изменения угловой скорости твердого тела. E=lim dW/dt при dtà0, где W-угловая скорость, t-время. Единица измерения(рад/с).
Равномерное вращение можно характеризовать периодом обращения T, под которым понимают время, за которое тело делает один оборот. dt=T, dФ=2П, то W=2П/Т откуда Т=2П/W, v=W/2П => W=2Пv
Первый закон Ньютона (закон инерции)
Всякое тело сохраняет состяние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.
Момент импулься и момент силы.Уравнение моментов.Закон сохранения моментов импульса.Гироскопические явления.
Если на тело действует М(момент силы), то 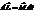 ,
,
L- импульс момента силы. 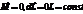 .
.
В замкнутой системе полный момент импульса тела постоянная величина.
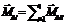
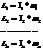 =>
=> 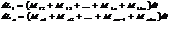
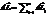
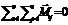
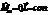
Свободные оси вращения тел.Для любого тела можно выделить 3 оси его вращения. Любое тело обладающее большой массой, способное вращаться относительно одной из своих осей называется гироскоп. Применение гироскопа (самолеты, ракеты корабли)

M=mgl*sin 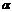 ; M
; M 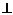 h
h 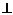 mg;
mg; 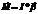 ; Mdt=dL; M и L сонаправлены
; Mdt=dL; M и L сонаправлены 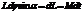
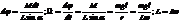
Скорость процессии(поворот вокруг вертикальной оси)
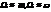
И абсолютно твердого тела.
Механическая энергия – это мера движения частиц механической системы. Она складывается из энергии движения (кинетической) и энергии взаимодействия (потенциальной)
Кинетическая энергия тела – это энергия, представляющая меру его механического движения и измеряемая той работой, которую может совершить тело при его торможении до полной остановки.
Поступательное движение
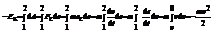 ;
; 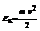 ,кинетическая энергия поступательно движущегося тела равна половине произведения массы этого тела на квадрат его скорости.
,кинетическая энергия поступательно движущегося тела равна половине произведения массы этого тела на квадрат его скорости.
Вращательное движение 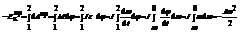 ;
; 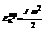 , кинетическая энергия вращающегося тела равна половине произведения момента инерции этого тела на квадрат его угловой скорости.
, кинетическая энергия вращающегося тела равна половине произведения момента инерции этого тела на квадрат его угловой скорости.
Барометрическая формула
Давление на высоте h равно 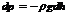
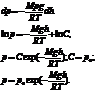
Распределение Больцмана
Заменим в показателе экспоненты отношение M/R равным ему отношением m/k(m масса молекулы, k-пост Больцмана).Заменим p на nkT.Сократим на kT:
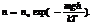
При Абсолютном нуле все молекулы расположились бы на земной поверхности.
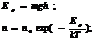
Виды теплоемкости
Если нагревать тело при постоянном давлении, то оно будет расширяться и совершать работу. Для нагревания тела на 1К при постоянном давлении ему нужно передать большее количество теплоты, чем при таком же нагревании при постоянном объеме. Для жидких и твердых тел эта разница несущественна, а вот газы сильно расширяются, и поэтому для газов различают теплоемкость при постоянном объеме и теплоемкость при постоянном давлении.
А) Теплоемкость газа при постоянном объеме
С=Q/ ΔT (определение)
Для процесса при постоянном объеме:
Qv=CvΔT
При постоянном объеме работа не совершается. Поэтому первый закон термодинамики запишется так:
CvΔT= ΔU
Для одного моля разреженного газа ΔU=1,5RΔT.Следовательно теплоемкость при постоянном объеме одноат. газа равна: Cv=1,5R
Б) Теплоемкость газа при постоянном давлении
Qp=CpΔT
Работа, которую совершит 1моль идеального газа, расширяющегося при постоянном давлении, равна A´=RΔT.
Это следует из выражения для работы газа при постоянном давлении A´=pΔVи уравнения состояния (для 1моля) идеального газа pV=RT.
Внутренняя энергия ид. газа от объема не зависит. Поэтому и при постоянном давлении изменение внутр. энергии ΔU=CvΔT, как и при постоянном объеме. Применяя первый закон термодинамики, получим:
CpΔT=CvΔT+RΔT
Следовательно, Cp=Cv+R
В случае идеального одноатомного газа Cp=1,5R+R=2,5R
Пуассона
Энтропия. Свойства энтропии
Клаузиус предложил связь между теплотой и температурой:
dS = dQ / T. dS – энтропия
dQ = dU + dA; dQ = CvdT + PdV; dQ = CvdT + RTdV/V;
dQ/ T = CvdT/ T + RdV/V; dS = Cvd(ln T) + Rd(ln V); TdS=dU+dA;
Свойства энтропии:
1) Энтропия изолированной системы при протекании необратимого процесса возрастает
2) Энтропия системы, находящейся в равновесном состоянии, максимальна
Энтропия при необратимом процессе:
Формула dS = dQ / T применима только к обратимым процессам. Для того чтобы найти изменение энтропии при необратимом процессе, поступают след образом. Рассматривают какой-либо обратимый процесс, приводящий систему в то же конечное состояние, что и данный необратимый процесс, и вычисляют для этого процесса приращение энтропии по формуле
S2 – S1 = 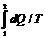
37.Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реальных газов. Эффект Джоуля-Томсона. Фазовые превращения.
Прежде всего надо принять во внимание то, что если частицы имеют конечные размеры, то сжать газ так, чтобы объем области, в котором он находился, уменьшился до нуля, уже нельзя. Если представить молекулы в виде шариков конечных размеров и рассмотреть газ в цилиндре под поршнем, то легко понять, что двигать поршень в сторону дна цилиндра можно только до тех пор, пока под ним не окажется совокупность плотно уложенных шариков - молекул. Для того чтобы еще дальше уменьшать свободный объем под поршнем, надо начать сжимать сами эти шарики, что, конечно, потребует несравненно больших усилий.
Уравнение состояния идеального газа pV = RT, можно сохранить и в том случае, когда предполагается, что частицы обладают определенным общим объемом. Для этого надо учесть, что реальное изменение объема под поршнем в цилиндре может проводиться не до нуля, а только до некоторой величины b, Уравнение состояния тогда перепишется в виде p(V - b) = RT.
Другим отличием реальных газов от идеального является наличие межмолекулярных взаимодействий, среди которых основную роль играют электростатические взаимодействия.
Уравнение состояния для реальных газов надо записать в следующей форме:
(р + Δр)(V - b) = RT.
Необходимо, чтобы частицы в среднем могли находиться на достаточно малых расстояниях друг от друга, что, очевидно, возможно только тогда, когда n0 достаточно велико. Напомним, что n0 - концентрация частиц. Следовательно, Δр должно возрастать с увеличением n0.
Так как число поверхностных частиц равно n0, то дополнительное давление Δр пропорционально n20 или 1/V2. Значит, в разложении Δр по обратным степеням объема прежде всего следует сохранить член a/V2. Таким образом, уравнение состояния газа может быть переписано в форме
(р + a/V2) (V - b) = RT
уравнение состояния реального газа в форме Ван - дер - Ваальса.
где а и b - некоторые постоянные коэффициенты, зависящие от сорта газа (b - коэффициент, пропорциональный общему объему всех частиц газа. а - коэффициент, связанный с межмолекулярными взаимодействиями между частицами газа).
При больших V это уравнение переходит в уравнение идеального газа.
Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
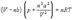 (1.5)
(1.5)
или для одного моля
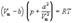 . (1.6)
. (1.6)
Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление
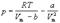 (1.7)
(1.7)
или объем
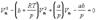 (1.8)
(1.8)
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.

На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3).
Эффект Джоуля – Томсона внутренняя энергия зависит только от температуры.
Криволинейное движение мат. точки
В зависимости от формы траектории различают прямолинейное движение, движение по окружности и криволинейное движение. Криволинейное движение – это движение по криволинейной траектории.При криволинейном движении вектор ускорения описывает изменение величины и направления скорости.
Ускорение – это величина, определяемая формулой w=dv/dt.
Тангенциальное ускорение –вектор,характеризующий изменение скорости по времени,направленный по касательной к траектории,численно равный 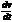
 Нормальное ускорение-вектор,характеризующий изменение скорости по направлению и направленный по разиусу к центру криволин.траектории.Численно равен
Нормальное ускорение-вектор,характеризующий изменение скорости по направлению и направленный по разиусу к центру криволин.траектории.Численно равен 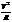
Предел отношения 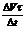 при
при 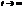 называется тангенциальным(касательным ускорением).
называется тангенциальным(касательным ускорением).
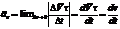
Предел отношения 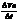 при
при 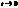 называется нормальным(центростремительным ускорением).
называется нормальным(центростремительным ускорением).
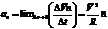 или
или 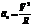
где R-радиус кривизны траектории.
Т.К. ускорения взаимно перпендикулярны:
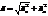
3.Движение точки по окружности.Угловое перемещение,скорость,ускорение.Связь между линейными и угловыми характеристиками.
 1)Вращательное движение-движение тела вокруг неподвижной оси,при котором все точки тела движутся по окружности,центры которых лежат на одной прямой-ось вращения
1)Вращательное движение-движение тела вокруг неподвижной оси,при котором все точки тела движутся по окружности,центры которых лежат на одной прямой-ось вращения
Угловая скорость
Угловая скорость –векторная
величина W, характеризующая
быстроту вращения твердого тела
и направленная по правилу
правого винта.
W=lim dФ/dt при dtà0, где Ф- угол поворота, t-время. Единица измерения (рад/с). Вращение с постоянной угловой скоростью называется равномерным. Если вращение является равномерным, тоW=Ф/t, где Ф- конечный угол поворота за время t.
Угловое ускорение
Угловое ускорение - векторная величина Е, Характеризующая быстроту изменения угловой скорости твердого тела. E=lim dW/dt при dtà0, где W-угловая скорость, t-время. Единица измерения(рад/с).
Равномерное вращение можно характеризовать периодом обращения T, под которым понимают время, за которое тело делает один оборот. dt=T, dФ=2П, то W=2П/Т откуда Т=2П/W, v=W/2П => W=2Пv
