Работа. Первое начало термодинамики. Циклы.
65. Какая работа А совершается при изотермическом расширении водорода массой m=5 г, взятого при температуре Т=290 К, если объем газа увеличивается в три раза?
66. Определить работу А адиабатного расширения водорода массой m=4 г, если температура газа понизилась на 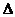 Т = 10 К.
Т = 10 К.
67. Баллон вместимостью V=20 л содержит водород при температуре Т=300 К под давлением р = 0,4 МПа. Каковы будут температура 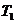 и давление
и давление 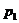 . Если газу сообщить количество теплоты Q= 6 кДж?
. Если газу сообщить количество теплоты Q= 6 кДж?
68. Кислород при неизменном давлении р = 80кПа нагревается. Его объем увеличивается от 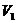 =1 м
=1 м 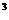 до
до 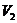 = 3 м
= 3 м 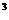 . Определить: 1) изменение
. Определить: 1) изменение 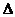 U внутренней энергии кислорода; 2) работу А, совершенную им при расширении; 3) количество теплоты Q , сообщенное газу.
U внутренней энергии кислорода; 2) работу А, совершенную им при расширении; 3) количество теплоты Q , сообщенное газу.
69. При изотермическом расширении водорода массой m=1 г, имевшего температуру Т= 280 К, объем газа увеличился в три раза. Определить работу А расширения газа и полученное газом количество теплоты Q.
70. Углекислы газ СО 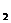 массой m=400 г был нагрет на
массой m=400 г был нагрет на 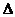 Т = 50 К при постоянном давлении. Определить изменение
Т = 50 К при постоянном давлении. Определить изменение 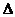 U внутренней энергии газа, количество теплоты Q , полученное газом, и совершенную им работу А.
U внутренней энергии газа, количество теплоты Q , полученное газом, и совершенную им работу А.
71. Кислород массой m=800 г, охлажденный от 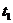 =100 С до температуры
=100 С до температуры 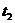 = 20 С, сохранил неизменный объем V. Определить: 1) количество теплоты Q , полученное газом; 2) изменение
= 20 С, сохранил неизменный объем V. Определить: 1) количество теплоты Q , полученное газом; 2) изменение 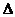 U внутренней энергии; 3) совершенную газом работу А.
U внутренней энергии; 3) совершенную газом работу А.
72. Азот массой m = 200 г расширяется изотермически при температуре Т= 280 К, причем объем газа увеличивается в два раза. Найти: 1) изменение 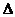 U внутренней энергии газа; 2) совершенную при расширении газа работу А; 3) количество теплоты Q , полученное газом.
U внутренней энергии газа; 2) совершенную при расширении газа работу А; 3) количество теплоты Q , полученное газом.
73. Какое количество теплоты Q выделится, если азот массой m=1 г, взятый при температуре Т= 280 К под давлением 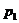 = 0,1 МПа, изотермически сжать до давления
= 0,1 МПа, изотермически сжать до давления 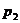 = 1 МПа?
= 1 МПа?
74. При адиабатном расширении кислорода с начальной температурой 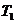 = 320 К внутренняя энергия уменьшилась на
= 320 К внутренняя энергия уменьшилась на 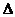 U= 8,4 кДж, а его объем увеличился в n=10 раз. Определить массу m кислорода.
U= 8,4 кДж, а его объем увеличился в n=10 раз. Определить массу m кислорода.
75. Идеальный газ совершает цикл Карно. Температура 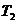 охладителя равна 290 К. Во сколько раз увеличится КПД цикла, если температура нагревателя повысится от
охладителя равна 290 К. Во сколько раз увеличится КПД цикла, если температура нагревателя повысится от 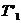 = 400 К до
= 400 К до 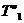 =600 К?
=600 К?
76. Идеальный газ, совершающий цикл Карно, получив от нагревателя количество теплоты Q 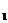 = 4,2 кДж, совершил работу А=590 Дж. Найти термический КПД
= 4,2 кДж, совершил работу А=590 Дж. Найти термический КПД 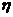 этого цикла. Во сколько раз температура
этого цикла. Во сколько раз температура 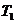 нагревателя больше температуры
нагревателя больше температуры 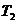 охладителя?
охладителя?
77. Совершая замкнутый процесс, газ получил от нагревателя количество теплоты Q 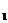 = 4 кДж. Определить работу А газа при протекании цикла, если его термический КПД
= 4 кДж. Определить работу А газа при протекании цикла, если его термический КПД 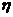 =0,1.
=0,1.
Энтропия
78. Найти изменение 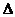 S энтропии при изобарном расширении азота массой m=4 г от объема V
S энтропии при изобарном расширении азота массой m=4 г от объема V 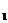 =5 л до объема V
=5 л до объема V 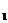 =9 л.
=9 л.
79. Лед массой m 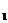 =2 кг при температуре t
=2 кг при температуре t 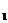 =0
=0 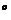 C был превращен в воду той же температуры с помощью пара, имеющего температуру t
C был превращен в воду той же температуры с помощью пара, имеющего температуру t 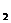 =100
=100 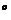 C. Определить массу m
C. Определить массу m 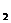 израсходованного пара. Каково изменение
израсходованного пара. Каково изменение 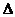 S энтропии системы лед-пар?
S энтропии системы лед-пар?
80. Кислород массой m=2 кг увеличил свой объем в n=5 раз один раз изотермически, другой - адиабатно. Найти изменения энтропии в каждом из указанных процессов.
81. Водород массой m=100 г был изобарно нагрет так, что объем его увеличился в n=3 раза, затем водород был изохорно охлажден так, что его давление уменьшилось в n=3 раза. Найти изменение 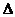 S энтропии в ходе указанных процессов.
S энтропии в ходе указанных процессов.
Реальные газы. Жидкости.
82. В сосуде вместимостью V=0,3 л находится углекислый газ, содержащей количество вещества 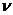 =1 моль при температуре Т=300 К. Определить давление р газа: 1)по уравнению Менделеева – Клапейрона; 2) по уравнению Ван-дер-Ваальса.
=1 моль при температуре Т=300 К. Определить давление р газа: 1)по уравнению Менделеева – Клапейрона; 2) по уравнению Ван-дер-Ваальса.
83. Давление р кислорода равно 7 МПа, его плотность 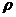 =100 кг/м
=100 кг/м 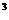 . Найти температуру Т кислорода.
. Найти температуру Т кислорода.
84. Трубка имеет диаметр d 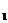 =0,2 см. На нижнем конце трубки повисла капля воды, имеющая в момент отрыва вид шарика. Найти диаметр d
=0,2 см. На нижнем конце трубки повисла капля воды, имеющая в момент отрыва вид шарика. Найти диаметр d 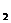 этой капли.
этой капли.
85. Какую работу А нужно совершить, чтобы, выдувая мыльный пузырь, увеличить его диаметр от d 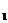 =1 см до d
=1 см до d 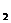 =11 см? Считать процесс изотермическим.
=11 см? Считать процесс изотермическим.
86.Капиллярная трубка диаметром d=0,5 мм наполнена водой. На нижнем конце трубки вода повисла в виде капли. Эту каплю можно принять за часть сферы радиуса r=3 мм. Найти высоту h столбика воды в трубке.
87. На сколько давление р воздуха внутри мыльного пузыря больше атмосферного давления р 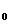 , если диаметр пузыря d=5 мм?
, если диаметр пузыря d=5 мм?
Примеры решений.
1. Колесо вращается по закону 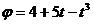 . Найти в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точек, лежащих на ооде колеса. Радиус колеса 2 см.
. Найти в конце первой секунды вращения угловую скорость колеса, а также линейную скорость и полное ускорение точек, лежащих на ооде колеса. Радиус колеса 2 см.
Решение. Согласно определению, угловая скорость
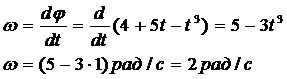 (1)
(1)
Линейная скорость
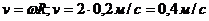
По определению, угловое ускорение 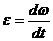 , или с учетом (1)
, или с учетом (1)
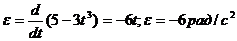 .
.
Полное линейное ускорение
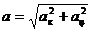 , где
, где
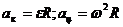 .
.
Тогда
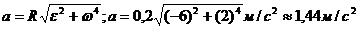
2. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
Решение. Рассмотрим движение каждого тела отдельно. На брусок действуют:
m  g- сила тяжести, N- сила нормальной реакции плоскости, Т
g- сила тяжести, N- сила нормальной реакции плоскости, Т  - сила натяжения нити, F
- сила натяжения нити, F 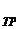 - сила трения. Запишем для бруска второй закон Ньютона:
- сила трения. Запишем для бруска второй закон Ньютона:
m  g+N+ Т
g+N+ Т  + F
+ F 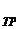 = m
= m  a
a  .
.
Спроецировав полученное уравнение на выбранные направления осей Х и Y , получим
Т  -F
-F 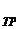 = m
= m 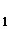 a
a  , (1)
, (1)
m  g-N=0. (2)
g-N=0. (2)
Так как из уравнения (2) следует, что N=m  g, то F
g, то F 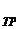 =
= 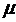 N=
N= 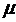 m
m  g. Тогда [см (1)]
g. Тогда [см (1)]
Т  -
- 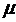 m
m  g = m
g = m  a
a  . (3)
. (3)
На груз действуют:
m  g- сила тяжести, Т
g- сила тяжести, Т  - сила натяжения нити. Запишем для груза второй закон Ньютона:
- сила натяжения нити. Запишем для груза второй закон Ньютона:
m  g+ Т
g+ Т  =m
=m  a
a  (4).
(4).
Спроецировав уравнение (4) на ось Y, получим
m  g- Т
g- Т  =m
=m  a
a  . (5)
. (5)
Складывая уравнения (3) и (5) и учитывая, что Т  = Т
= Т  =Т, а a
=Т, а a  = a
= a  =а, получаем m
=а, получаем m  g-Т+Т-
g-Т+Т- 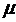 m
m  g=( m
g=( m  + m
+ m  ) а, откуда
) а, откуда
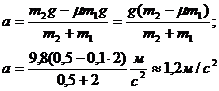 .
.
Силу натяжения нити находим из уравнения (5):
Т  =m
=m  g- m
g- m  a
a  = m
= m  (g-a);
(g-a);
T=0,5(9,8-1,2)H 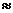 4,3H
4,3H
3. Снаряд массой 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью 500 м/с, попадает в вагон с песком массой 10 т и застревает в нем. Найти скорость вагона, если он двигался со скоростью 36 км/ч навстречу снаряду.
Решение. Запишем для снаряда и вагона с песком закон сохранения импульса при неупругом ударе:
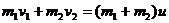 (1)
(1)
Выбирая направление оси Х совпадающим с направлением движения снаряда и проецируя на нее обе части уравнения (1), получаем
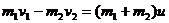 , откуда
, откуда
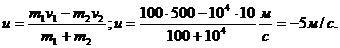
Следовательно, направление движения вагона не изменилось.
4. Маховик в виде диска массой m=50 кг и радиусом r=20 см был раскручен до частоты вращения n=480 мин 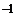 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным, если маховик остановился через t=50c.
и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным, если маховик остановился через t=50c.
Решение. По второму закону динамики вращательного движения твердого тела имеем:
M 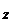 =J
=J 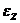 , где J- момент инерции маховика, M
, где J- момент инерции маховика, M 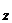 и
и 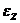 - момент силы трения и угловой ускорения, спроецированные на ось вращения.
- момент силы трения и угловой ускорения, спроецированные на ось вращения.
Движение равнозамедленное, поэтому угловая скорость изменяется по закону 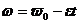 , где
, где 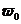 - начальная угловая скорость,
- начальная угловая скорость, 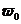 =2
=2 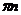 , конечная угловая скорость
, конечная угловая скорость 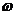 =0, отсюда,
=0, отсюда, 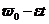 =0,
=0, 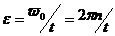 .
.
Момент инерции диска относительно оси проходящей через центр инерции равен:
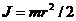 . Подставляя выражения J и
. Подставляя выражения J и 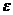 в формулу (1), получаем:
в формулу (1), получаем:
M 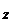 =
= 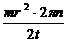
Результат расчета в СИ дает тормозящий момент сил трения M=1Hм.
5. Определить плотность смеси, состоящей из 4 г водорода и 32 г кислорода, при температуре 7 С и давлением 93 Па.
Решение. По закону Дальтона, давление смеси
р = р 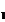 + р
+ р 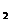 (1) , где р
(1) , где р 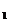 и р
и р 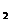 - парциальные давления водорода и кислорода при данных условиях. Запишем уравнение Клапейрона –Менделеева для каждого газа в отдельности;
- парциальные давления водорода и кислорода при данных условиях. Запишем уравнение Клапейрона –Менделеева для каждого газа в отдельности;
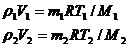
По условию задачи, V 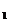 =V
=V 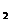 =V, T
=V, T 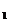 =T
=T 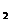 =T.
=T.
Тогда для водорода 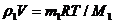 (2)
(2)
Аналогично для кислорода- 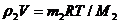 (3)
(3)
Подставим выражения (2), (3) в (1):
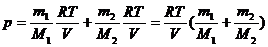
Откуда 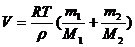 (4)
(4)
По определению, плотность смеси газов 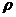 = m/V (5), где
= m/V (5), где
m=m 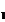 + m
+ m 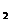 - масса смеси и газов.
- масса смеси и газов.
Подставим выражение (4) в (5):
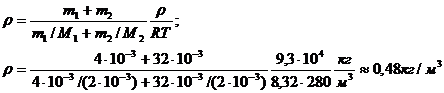
6. Средняя длина свободного пробега <l> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <v> молекул и число z соударений, которые испытывает молекула в 1 с.
Решение. Средняя арифметическая скорость молекул определяется по формуле 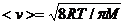 , где М- молярная масса вещества.
, где М- молярная масса вещества.
Подставив числовые значения числовые значения, получим 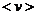 =362 м/с.
=362 м/с.
Среднее число <z> соударений молекулы в 1 с определяется отношением средней скорости <v> молекулы к средней длине ее свободного пробега <l>:
<z>=<v>/<l>.
Подставив в эту формулу значения <v>=362 м/с, <l>=40 нм=4 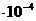 м, получим
м, получим
<z>=9,05 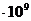 c
c 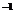
7. Углекислый газ массой 10 г нагрет от 20 до 30 С при постоянном давлении. Найти работу расширения газа и изменение его внутренней энергии.
Решение. Изменение внутренней энергии углекислого газа при его нагревании от температуры Т  до температуры Т
до температуры Т  найдем по формуле
найдем по формуле
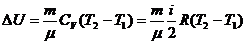 , где m- масса газа,
, где m- масса газа, 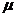 - молярная масса газа (
- молярная масса газа ( 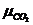 =44
=44 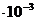 кг/моль), i- число степеней свободы, i=6 для трехатомного газа,
кг/моль), i- число степеней свободы, i=6 для трехатомного газа,
R=8,31 Дж/моль К- газовая постоянная, Т  и Т
и Т  - температура газа начальная и конечная по шкале Кельвина.
- температура газа начальная и конечная по шкале Кельвина.
Подставляя данные в СИ, получаем 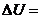 83 Дж.
83 Дж.
Работа расширения углекислого газа
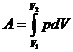 (1)
(1)
По условию задачи, давление углекислого газа p=const. Тогда давление, как постоянную величину, можно вынести из под знака интеграла и выражение (1) примет вид
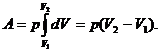
Из уравнения Клапейрона - Менделеева
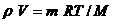
Находим объем углекислого газа при температуре Т:
V=mRT/(Mp). Следовательно, при температурах Т  и Т
и Т  углекислый газ будет занимать объемы
углекислый газ будет занимать объемы
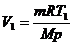 и
и 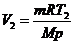 .
.
Подставим выражения (3) в (1):
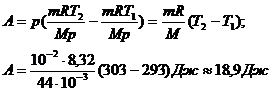
8. Определить изменение 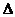 S энтропии при изотермическом расширении кислорода массой m=10 г от объема V
S энтропии при изотермическом расширении кислорода массой m=10 г от объема V 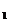 =25 л до объема V
=25 л до объема V 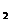 =100 л.
=100 л.
Решение. Так как процесс изотермический, то в общем выражении энтропии 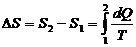 температуру выносят за знак интеграла. Выполнив это, получим
температуру выносят за знак интеграла. Выполнив это, получим 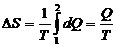 . (1)
. (1)
Количество теплоты Q, полученное газом, найдем по первому началу термодинамики 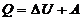 . Для изотермического процесса
. Для изотермического процесса 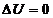 , следовательно, Q=A, (2)
, следовательно, Q=A, (2)
а работа А для этого процесса определяется по формуле
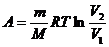 . (3)
. (3)
С учетом (2) и (3) равенство (1) примет вид
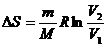 . (4)
. (4)
Подставив в (4) числовые значения и произведя вычисления, получим 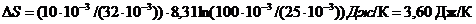
9. Определить изменение свободной энергии 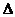 Е поверхности мыльного пузыря при изотермическом увеличении его объема V
Е поверхности мыльного пузыря при изотермическом увеличении его объема V 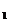 =10 см
=10 см 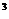 до V
до V 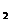 =2V
=2V 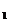 .
.
Решение. Свободная энергия Е поверхности жидкости пропорциональна площади S этой поверхности: E= 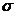 S, (1)
S, (1)
где 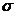 - поверхностное натяжение.
- поверхностное натяжение.
У мыльного пузыря имеются две поверхности – внешняя и внутренняя, площади которых фактически равны из-за малой толщины мыльной пленки. Поэтому свободная энергия поверхности (внешней и внутренней вместе) мыльного пузыря:
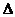 E=2
E=2 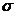
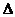 S (2)
S (2)
Где 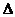 S- изменение поверхности пузыря (одной – внутренней или внешней).
S- изменение поверхности пузыря (одной – внутренней или внешней).
Считая, что мыльный пузырь имеет форму сферы, найдем изменение площади поверхности:
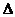 S=
S= 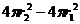 , (3)
, (3)
где r 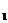 и r
и r 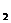 - радиусы сфер, соответствующие изначальному V
- радиусы сфер, соответствующие изначальному V 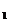 и конечному V
и конечному V 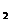 объемам:
объемам: 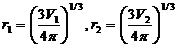 . Теперь формула (3) примет вид
. Теперь формула (3) примет вид 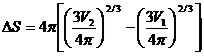 . Учитывая, что V
. Учитывая, что V 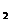 =2V
=2V 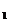 :
: 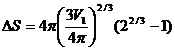 .
.
Подставим выражение 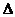 S в формулу (2):
S в формулу (2):
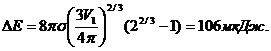
Ответы 

Кинематика
1) 8,7 м/с
2) 40 с, 80 м, - 0,1 м/с 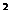
3) 14,1 м/с, -10 м/с 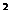 , 7,07 м/с
, 7,07 м/с 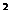 , -7,07 м/с
, -7,07 м/с 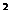
4) 2 м/с 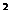 , 1 м/с
, 1 м/с 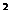 , 2,24 м/с
, 2,24 м/с 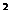
5) 7 м/с, 8,5 М
6) 9б62 м, 14,6 м/с
7) 1,53 км, 3,53 км, 1,02 км
8) 3,58 м/с, 5,37 м/с 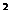 , 8,22 м/с
, 8,22 м/с 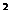
9) -0,523 м/с 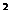 , 150
, 150
10) 1,261 1/с