Кинетическая энергия вращающегося тела

Выражение для кинетической энергии 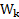вращающегося тела с учетом, что линейная скорость произвольной материальной точки, составляющей тело, относительно оси вращения равна 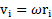имеет вид

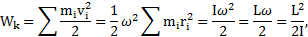
где 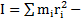момент инерции тела относительно выбранной оси вращения, 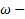его угловая скорость относительно этой оси, 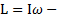момент импульса тела относительно оси вращения.

Если тело совершает поступательно вращательное движение, то вычисление кинетической энергии зависит от выбора полюса, относительно которого описывается движение тела. Конечный результат будет один и тот же. Так, если для катящегося со скоростью vбез проскальзывания круглого тела с радиусом R и коэффициентом инерции k полюс взять в его ЦМ, в точке C, то его момент инерции 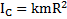, а угловая скорость вращения вокруг оси С 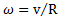. Тогда кинетическая энергия тела .

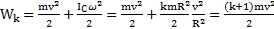Если полюс взять в точке О касания тела и поверхности, через которую проходит мгновенная ось вращения тела, то его момент инерции относительно оси О станет равным 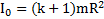. Тогда кинетическая энергия тела с учетом, что относительно параллельных осей угловые скорости вращения тела одинаковы и вокруг оси О тело совершает чистое вращение, будет равна 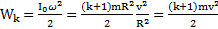. Результат тот же.

Теорема о кинетической энергии тела, совершающего сложное движение, будет иметь такой же вид, что и для его поступательного движения: .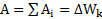

Пример 1.К концу нити, накрученной на цилиндрический блок радиуса R и массой M, привязано тело массой m. Тело поднимают на высоту h и отпускают (рис.65). После неупругого рывка нити тело и блок сразу же начинают двигаться совместно. Какое тепло выделится при рывке? Чему будут равны ускорение движения тела и натяжение нити после рывка? Какими будут скорость тела и пройденный им путь после рывка нити через время t?

Дано: M, R, m, h, g, t. Найти: Q -?,a - ?, T - ?,v -?, s - ?

Решение: Скорость тела перед рывком нити 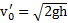. После рывка нити блок и тело придут во вращательное движение относительно оси блока О и будут вести себя как тела с моментами инерции относительно этой оси, равными 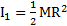и . И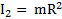х общий момент инерции относительно оси вращения .

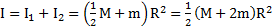Рывок нити – быстрый процесс и при рывке имеет место закон сохранения момента импульса системы блок-тело, который ввиду того, что тело и блок сразу же после рывка начинают двигаться совместно, имеет вид: 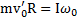. Откуда начальная угловая скорость вращения блока 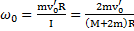, а начальная линейная скорость тела .

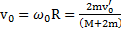Кинетическая энергия системы ввиду сохранения ее момента импульса 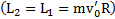сразу после рывка нити равна 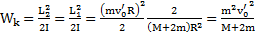. Выделившееся при рывке тепло согласно закону сохранения энергии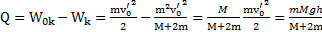

Динамические уравнения движения тел системы после рывка нити не зависят от их начальной скорости. Для блока оно имеет вид 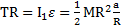или 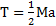, а для тела 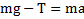. Складывая эти два уравнения, получим 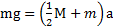. Откуда ускорение движения тела 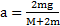. Сила натяжения нити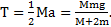

Кинематические уравнения движения тела после рывка будут иметь вид 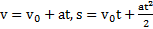, где все параметры известны.

Ответ: . .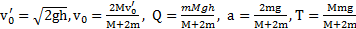

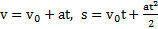Пример 2. Двум круглым телам с коэффициентами инерции 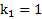(полый цилиндр) и 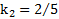(шар), находящимся в основании наклонной плоскости с углом наклона α сообщают одинаковые начальные скорости, направленные вверх вдоль наклонной плоскости. На какую высоту и за какое время поднимутся тела на эту высоту? Каковы ускорения подъема тел? Во сколько раз отличаются высоты, времена и ускорения подъема тел? Тела движутся вдоль наклонной плоскости без проскальзывания.

Рис.67

Дано: 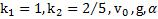. Найти: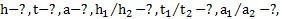

Решение: На тело действуют: сила тяжести mg, реакция наклонной плоскости N, и сила трения сцепления 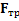(рис.67). Работы нормальной реакции и силы трения сцепления (нет проскальзывания и в точке сцепления тела и плоскости тепло не выделяется.) равны нулю: 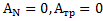, поэтому для описания движения тел возможно применение закона сохранения энергии: 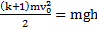. Откуда .

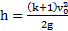Времена и ускорения движения тел найдем из кинематических уравнений 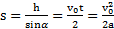. Откуда 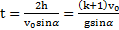, 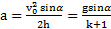. Отношение высот, времен и ускорений подъема тел: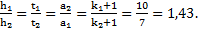

Ответ: , , , .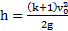

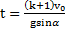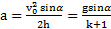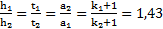Пример 3. Пуля массой 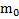, летящая со скоростью 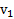, ударяет в центр шара массой M и радиусом R, прикрепленному к концу стержня массой mи длиной l, подвешенному в точке О за его второй конец, и вылетает из него со скоростью 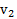(рис.68). Найти угловую скорость вращения системы стержень-шар сразу же после удара и угол отклонения стержня после удара пули.

Рис.68

Дано: 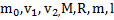. Найти: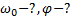

Решение:Моменты инерции стержня и шара относительно точки О подвеса стержня по теореме Штейнера: 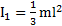и 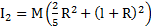. Полный момент инерции системы стержень-шар 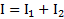. Удар пули – быстрый процесс, и имеет место закон сохранения момента импульса системы пуля-стержень-шар (тела после столкновения приходят во вращательное движение): 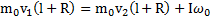. Откуда угловая скорость движения системы стержень-шар сразу же после удара .

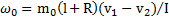Положение ЦМ системы стержень-шар относительно точки подвеса О: 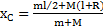. Закон сохранения энергии для ЦМ системы после удара с учетом закона сохранения момента импульса системы при ударе имеет вид 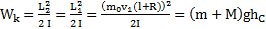. Откуда высота поднятия ЦМ системы после удара 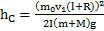. Угол отклонения стержня после удара определяется условием .

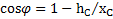Ответ: , , .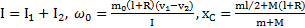

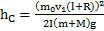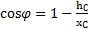Пример 4. К круглому телу массой m и радиусом R, с коэффициентом инерции k, вращающемуся с угловой скоростью 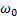, прижата с силой N колодка (рис.69). Через какое время остановится цилиндр и какое тепло выделится при трении колодки о цилиндр за это время? Коэффициент трения между колодкой и цилиндром равен .

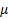Рис.69

Дано: 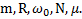Найти: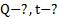

Решение: Работа силы трения до остановки тела по теореме о кинетической энергии равна 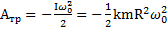. Выделившееся при вращении тепло .

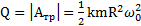Уравнение вращательного движения тела 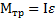имеет вид 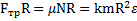. Откуда угловое ускорение его замедленного вращения 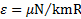. Время вращения тела до его остановки .

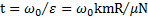Ответ: , .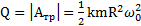

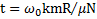Пример 5. Круглое тело массой m и радиусом R с коэффициентом инерции k раскручивают до угловой скорости 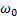против часовой стрелки и ставят на горизонтальную поверхность, стыкующуюся с вертикальной стенкой (рис.70). Через какое время тело остановится и сколько оно сделает оборотов до остановки? Чему будет равно тепло, выделившееся при трении тела о поверхности за это время? Коэффициент трения тела о поверхности равен .

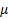Рис.70

Дано: 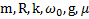. Найти: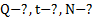

Решение: Тепло, выделившееся при вращении тела до его остановки, равно работе сил трения, которая может быть найдена по теореме о кинетической энергии тела. Имеем .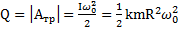

Реакция горизонтальной плоскости 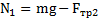. Силы трения, действующие на тело со стороны горизонтальной и вертикальной поверхностей равны: 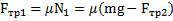и 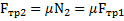.Из системы этих двух уравнений получим 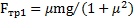и .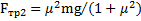

С учетом этих соотношений уравнение вращательного движения тела 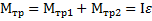имеет вид ( 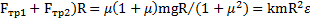. Откуда угловое ускорение вращения тела равно 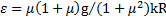. Тогда время вращения тела до его остановки 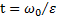, а число сделанных им при этом оборотов .

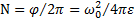Ответ: , , , .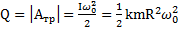

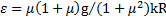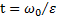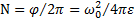Пример 6. Круглое тело с коэффициентом инерции k скатывается без проскальзывания с вершины полусферы радиусом R, стоящей на горизонтальной поверхности (рис.71). На какой высоте и с какой скоростью оно оторвется от полусферы и с какой скоростью упадет на горизонтальную поверхность?

Рис.71

Дано: k, g, R. Найти: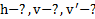

Решение: На тело действуют силы 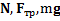. Работы 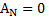и 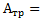0, (нет проскальзывания и тепло в точке сцепления полусферы и шара не выделяется) поэтому для описания движения тела возможно применение закона сохранения энергии. Второй закон Ньютона для ЦМ тела в точке его отрыва от полусферы с учетом, что в этой точке 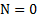имеет вид 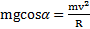, откуда 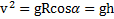. Закон сохранения энергии для начальной точки и точки отрыва тела имеет вид 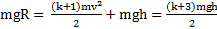. Откуда высота и скорость отрыва тела от полусферы равны , .

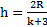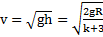После отрыва тела от полусферы изменяется только его поступательная кинетическая энергия, поэтому закон сохранения энергии для точек отрыва и падения тела на землю имеет вид 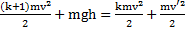. Откуда с учетом 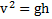получим 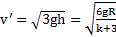. Для тела, скользящего по поверхности полусферы без трения, k=0 и , , .

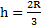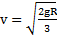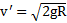Ответ: 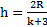, , .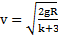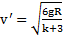