Полная механическая энергия тела. Закон сохранения полной механической энергии
Если все внешние силы, действующие на тело, разделить на консервативные и неконсервативные, то теорему о кинетической энергии тела можно переформулировать в терминах полной механической энергии тела. Учитывая, что 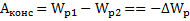 , получим для работы результирующей силы
, получим для работы результирующей силы
 .
.
Откуда
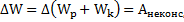 ,
,
где введена величина 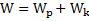 , называемая полной механической энергией тела. Полученное соотношение называют теоремой о полной механической энергии тела.
, называемая полной механической энергией тела. Полученное соотношение называют теоремой о полной механической энергии тела.
Если тело движется только в поле консервативных сил (неконсервативные силы отсутствуют или их работа равна нулю), то 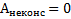 и
и 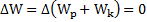 или
или  . Это закон сохранения полной механической энергии.
. Это закон сохранения полной механической энергии.
Теоремы о кинетической энергии тела 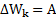 и полной энергии тела
и полной энергии тела 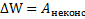 являются различными формулировками одного и того же энергетического принципа и при решении задач можно пользоваться любой из них. При этом необходимо учитывать, что кинетическую энергию
являются различными формулировками одного и того же энергетического принципа и при решении задач можно пользоваться любой из них. При этом необходимо учитывать, что кинетическую энергию 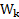 изменяют все силы, действующие на тело, а полную механическую энергию
изменяют все силы, действующие на тело, а полную механическую энергию 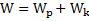 – только неконсервативные силы.
– только неконсервативные силы.
Пример 1. На наклонной плоскости, переходящей в основании в цилиндрическую поверхность радиуса R, вертикальный диаметр которой перпендикулярен основанию плоскости, находится тело (рис.44). С какой минимальной высоты оно должно скатиться, чтобы пройти верхнюю точку траектории и чему будет равна его скорость в этой точке? Трение между поверхностями и телом отсутствует.
Рис.44
Дано:R, g. Найти: 
Решение: Работа силы трения и нормальной реакции связи на всем пути движения тела равны нулю: 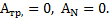 Поэтому возможно применение закона сохранения энергии. Для того чтобы тело прошло верхнюю точку, скатившись с минимальной высоты, необходимо, чтобы реакция поверхности в этой точке равнялась нулю
Поэтому возможно применение закона сохранения энергии. Для того чтобы тело прошло верхнюю точку, скатившись с минимальной высоты, необходимо, чтобы реакция поверхности в этой точке равнялась нулю  .
.
Имеем для закона сохранения энергии тела в начальной и верхней точках его траектории  и второго закона Ньютона в верхней точке
и второго закона Ньютона в верхней точке 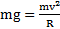 . Откуда приходим к системе двух уравнений:
. Откуда приходим к системе двух уравнений: 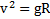 и
и  . Исключая
. Исключая  , получим
, получим  и
и  .
.
Ответ:  ,
,  .
.
Пример 2. Пружина с жесткостью k и длиной  , с прикрепленным к ней телом массой m, насажены на невесомый стержень. Второй конец стержня и пружины закреплены в одной точке (рис.45).Какую минимальную скорость надо сообщить телу, чтобы оно сделало полный оборот? Трение между телом и стержнем отсутствует.
, с прикрепленным к ней телом массой m, насажены на невесомый стержень. Второй конец стержня и пружины закреплены в одной точке (рис.45).Какую минимальную скорость надо сообщить телу, чтобы оно сделало полный оборот? Трение между телом и стержнем отсутствует.
Рис.45
Дано: m, k,  ,g. Найти:
,g. Найти: 
Решение:Чтобы тело сделало полный оборот при минимальной начальной скорости, необходимо, чтобы в верхней точке траектории реакция пружины была равна нулю  . Это означает, что в верхней точке траектории пружина не деформирована и ее длина равна
. Это означает, что в верхней точке траектории пружина не деформирована и ее длина равна  .
.
Условие равновесия тела в нижней точке  . Откуда
. Откуда 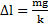 . Второй закон Ньютона для тела в верхней точке
. Второй закон Ньютона для тела в верхней точке 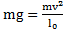 , откуда скорость тела в этой точке
, откуда скорость тела в этой точке 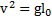 .
.
Тело находится в поле двух консервативных сил: силы тяжести и упругой силы, поэтому его полная потенциальная энергия равна 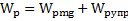 . Если выбрать нуль отсчета потенциальной энергии тела в поле силы тяжести в нижней точке его траектории, то закон сохранения для него в нижней и верхней точках траектории будет иметь вид
. Если выбрать нуль отсчета потенциальной энергии тела в поле силы тяжести в нижней точке его траектории, то закон сохранения для него в нижней и верхней точках траектории будет иметь вид
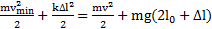 .
.
С учетом выражений для 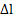 и
и  он примет вид
он примет вид 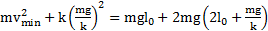 .Откуда
.Откуда
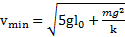 .
.
При отсутствии деформации пружины  ,
,  , и
, и  .
.
Ответ: 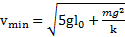 .
.
