Закон Стефана-Больцмана и закон Вина.
Задача нахождения функции Кирхгофа – это задача найти зависимость энергии излучения от температуры для различных частот. Решение было получено не сразу. Сначала был установлен теоретически и экспериментально закон зависимости суммарного излучения (энергетической светимости) черного тела от температуры (закон Стефана-Больцмана). Найден весьма точный экспериментальный вид зависимости испускательной способности от частоты и температуры (закон Вина). И, наконец, после ряда неудачных попыток, имеющих огромное значение для понимания вопроса, Планку удалось найти окончательное теоретическое решение задачи. Оно было найдено только путем решительного принципиального изменения основных положений физики, путем создания теории квантов, заложившей принципиально новую базу физической науки. Эта новая теория оказалась столь важной и плодотворной, что дальнейшее развитие ее составило главное содержание теоретической физики на все последующие годы и охватило почти все области науки.
В 1879 г. Стефан на основании анализа собственных измерений и данных других исследователей, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов.
В 1884 г. Больцман, исходя из термодинамических соображений, теоретически показал, что: энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры
 , (1.5)
, (1.5)
где σ – постоянная. Таким образом, вывод Стефана оказался справедлив лишь для абсолютно черных тел. Тщательные измерения, проведенные позднее для модели абсолютно черного тела, позволили подтвердить выводы Больцмана и определить постоянную σ. По современным измерениям σ =  . Соотношение между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана-Больцмана, а константа σ – постоянная Стефана-Больцмана.
. Соотношение между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана-Больцмана, а константа σ – постоянная Стефана-Больцмана.
В 1893 г. Вин теоретически получил ряд важных результатов. Одним из них является закон смещения Вина: частота, соответствующая максимальному значению испускательной способности абсолютно черного тела прямо пропорциональна его термодинамической температуре.
На графике (рис.1) положение максимума функции Кирхгофа смещается, согласно закону Вина, с повышением температуры в область больших частот. Площадь, охватываемая кривой, согласно соотношению (1.3), дает значение энергетической светимости абсолютно черного тела при данной температуре. Видно, что энергетическая светимость сильно

Рис.1 Распределение энергии в спектре абсолютно черного тела.
возрастает с увеличением температуры, что соответствует закону Стефана-Больцмана. Полученные Вином теоретические результаты полностью согласовывались с результатамиэкспериментов.
В практических целях часто используется другая форма закона смещения Вина: длина волны  , соответствующая максимальному значению испускательной способности абсолютно черного тела, обратно пропорциональна его термодинамической температуре
, соответствующая максимальному значению испускательной способности абсолютно черного тела, обратно пропорциональна его термодинамической температуре
 (1.6)
(1.6)
Экспериментальное значение константы b =2,90∙10-3 м∙ К.
5. Формула Рэлея-Джинса. Ультрафиолетовая катастрофа.
Окружим излучающее тело идеально отражающей оболочкой. В этом случае излучение, испускаемое телом, не будет рассеиваться по пространству, а, отражаясь стенками, сохранится в пределах полости, и, падая вновь на излучающее тело, поглотится им частично или полностью. Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы тело-излучение будет равновесным.
В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u = u(T). Спектральной распределение этой энергии можно охарактеризовать функцией 
 (1.7)
(1.7)
где duω – доля плотности энергии, приходящаяся на интервал частот dω.
Между равновесной плотностью энергии теплового излучения и испускательной способностью абсолютно черного тела существует следующая связь
 , (1.8) где c – скорость распространения электромагнитной волны в вакууме, т.е. скорость света.
, (1.8) где c – скорость распространения электромагнитной волны в вакууме, т.е. скорость света.
Д.Рэлей и Д.Джинс применили к тепловому излучению методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы получили формулу (без вывода)
 , (1.9)
, (1.9)
где kT – средняя энергия осциллятора с собственной циклической частотой.
Выражение (1.9) и называют формулой Релея-Джинса.
Эта формула удовлетворительно согласуется с экспериментальными данными лишь при малых частотах (больших длинах волн) и резко расходится для больших частот (малых длин волн). Интегрирование выражения (1.12) по ω в пределах от 0 до ∞ дает для энергетической светимости тела бесконечно большое значение (см. рис.2). Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Расхождение формулы Релея-Джинса с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики (рис.2).

Рис.2
6. Формула Планка. В 1900 г. Планку удалось найти вид функции u(ω,T) (а следовательно и f(ω,T)), в точности соответствующей опытным данным и впервые дать теоретическое обоснование спектральным закономерностям черного излучения.
В своих расчетах Планк выбрал модель излучающей системы в виде совокупности линейных гармонических осцилляторов со всевозможными собственными частотами. (Напомним, что линейный гармонический осциллятор – это система, совершающая гармонические линейные колебания. Гармоническим осциллятором можно назвать: пружинный маятник, математический маятник, колебательный контур, электрический диполь, стоячую волну внутри полости). По классическим законам излучающий осциллятор может испустить за единицу времени любое количество энергии. При расчете совокупности гармонических осцилляторов, подчиняющимся классическим законам, Планк нашел для функции Кирхгофа, выражение уже известное как формула Рэлея-Джинса. Анализируя полученные результаты, он пришел к выводу, что причина неудачи лежит в неприменимости законов классической физики к атомным осцилляторам, и выдвинул так называемую квантовую гипотезу. Гармонический осциллятор с частотой ω может обладать только таким количеством энергии, в котором содержится целое число элементарных порций ћω. В соответствии с этой гипотезой и излучение осциллятора идет в виде отдельных порций, которые получили название квантов энергии. Величина кванта пропорциональна частоте излучения: ε = ћ ω.Коэффициент пропорциональности получил название постоянной Планка. Значение ћ, определенное из экспериментов, равно: ћ = 1,054 ·10 -34 Дж · с.
Учитывая, что распределение осцилляторов по возможным энергетическим состояниям подчиняется закону распределения Больцмана, средняя энергия осциллятора в соответствии с квантовой гипотезой
 (1.10)
(1.10)
Для плотности энергии получено выражение
 , (1.11)
, (1.11)
и в соответствии с (1.8) запишем окончательный вид функции Кирхгофа, полученный Планком
 (1.12)
(1.12)
Эта формула точно согласуется с экспериментальными данными во всем интервале частот от 0 до ∞.
В области малых частот (или больших длин волн) 

в результате чего формула Планка (1.12) переходит в формулу Рэлея-Джинса (1.9). Это показывает, что в области низких частот теория Планка не противоречит классической теории.
Можно убедиться в том, что формула Планка заключает в себе все упомянутые выше законы теплового излучения абсолютно черного тела, а именно законыСтефана-Больцмана и Вина.
Энергетическую светимость R абсолютно черного тела можно найти из интегрированием по частоте:

Вычислив интеграл, получим  , т.е. формулу Стефана-Больцмана. Формула Планка позволяет также вычислить экспериментально найденные константы σ и b, используя универсальные постоянные ħ, k и с.
, т.е. формулу Стефана-Больцмана. Формула Планка позволяет также вычислить экспериментально найденные константы σ и b, используя универсальные постоянные ħ, k и с.
Таким образом, формула Планка дает исчерпывающее описание равновесного теплового излучения.
Вопросы для самоконтроля:
1. Что такое тепловое излучение?
2. Что такое абсолютно черное тело?
3. Как и во сколько раз изменится энергетическая светимость черного тела, если его термодинамическая температура увеличится втрое?
4. В область каких длин волн сместится максимум испускательной способности абсолютно черного тела при уменьшении термодинамической температуры?
5. В чем состоит ультрафиолетовая катастрофа?
6. При каких условиях из формулы Планка можно получить формулу Рэлея-Джинса?
Лекция № 2.
КВАНТОВЫЕ СВОЙСТВА СВЕТА
План
1. Фотоэлектрический эффект.
2. Фотоны.
3. Эффект Комптона.
Фотоэлектрический эффект.
Квантовая гипотеза Планка привела в дальнейшем к представлению о том, что свет не только испускается, но и поглощается отдельными порциями – квантами. Она нашла свое подтверждение и дальнейшее развитие в ряде явлений таких, как фотоэффект, эффект Комптона и др.
Внешним фотоэффектом называется испускание электронов веществом под действием света. Впервые Герц в 1887 г. обнаружил, что проскакивание искры между шариками разрядника значительно облегчается, если один из шариков осветить ультрафиолетовым светом. Это явление, как показали опыты А.Г.Столетова (1888-1890), обусловлено выбиванием под действием света отрицательных зарядов из металлического катода разрядника. На основании своих опытов Столетов пришел к следующим выводам: 1) наибольшее действие оказывают ультрафиолетовые лучи; 2) сила тока возрастает с увеличением освещенности пластины; 3) испускаемые под действием света заряды имеют отрицательный знак.
Для изучения фотоэффекта пользуются вакуумной трубкой. Катод в фотоэлементе Ф, покрытый исследуемым металлом, освещается монохроматическим светом. Внутри трубки поддерживается высокий вакуум, так как присутствие газов осложняет условия выхода и переноса зарядов. Между анодом и катодом с помощью батареи создается разность потенциалов. Электроны, освобожденные светом, под действием напряжения между анодом и катодом, движутся на анод и далее следуют по проводам через гальванометр Г, замыкая ток в цепи (см. рис.1).
 |
Рис.1
При неосвещенном катоде ток в цепи фотоэлемента отсутствует.
Зависимость фототока от напряжения можно представить в виде графика (рис.2)
 |
Рис.2
Существование фототока в области отрицательных напряжений объясняется тем, что фотоэлектроны обладают отличной от нуля кинетической энергией. За счет уменьшения этой энергии они могут совершать работу против сил задерживающего электрического поля в трубке и достигать анода. Максимальная начальная скорость фотоэлектронов υmax связана с величиной задерживающего напряжения Uзад соотношением
 (2.1)
(2.1)
где e и m – заряд и масса электрона.
При  фототок равен нулю. По мере увеличения напряжения ток постепенно возрастает, так как все большее число фотоэлектронов достигает анода. Максимальное значение силы тока Iн называется фототоком насыщения и соответствует таким значениям напряжения, при которых все электроны, выбиваемые из катода, достигают анода.
фототок равен нулю. По мере увеличения напряжения ток постепенно возрастает, так как все большее число фотоэлектронов достигает анода. Максимальное значение силы тока Iн называется фототоком насыщения и соответствует таким значениям напряжения, при которых все электроны, выбиваемые из катода, достигают анода.
Опытным путем установлены следующие основные законы фотоэффекта:
1. Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.
2. Для каждого вещества существует красная граница фотоэффекта, т.е. характерная минимальная частота света ω0 (или максимальная длина волны λ0), при которой еще возможен фотоэффект. Красная граница зависит от химической природы вещества и состояния его поверхности.
3. Количество испускаемых с катода электронов пропорционально интенсивности светового излучения (фототок насыщения пропорционален энергетической освещенности катода).
При объяснении первого и второго законов встретились серьезные трудности. Согласно электромагнитной теории, вырывание свободных электронов из металла должно являться результатом их “раскачивания” в электрическом поле световой волны. Однако в этом случае непонятно, почему максимальная начальная скорость и кинетическая энергия вылетающих фотоэлектронов зависят от частоты света, а не от амплитуды колебаний вектора напряженности электрического поля и связанной с ней интенсивностью волны. Эти факты вызывали сомнения в универсальной применимости волновой теории света.
Законы фотоэффекта находят свое объяснение в рамках квантовой теории. В 1905 году Эйнштейн, изучая проблему возникновения и превращения света, использовал явление фотоэффекта как подтверждение своих идей. Энергетический баланс при фотоэффекте выражается уравнением Эйнштейна
 , (2.2)
, (2.2)
где 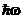 - энергия светового кванта, переданная электрону. Если эта энергия превышает энергию, необходимую для разрыва связи электрона с данным веществом (работу выхода А), то электрон покидает поверхность вещества, обладая кинетической энергией, максимально возможное значение которой определяется из уравнения Эйнштейна.
- энергия светового кванта, переданная электрону. Если эта энергия превышает энергию, необходимую для разрыва связи электрона с данным веществом (работу выхода А), то электрон покидает поверхность вещества, обладая кинетической энергией, максимально возможное значение которой определяется из уравнения Эйнштейна.
Таким образом, внешний фотоэффект возможен только в том случае, когда энергия фотона 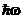 больше или, в крайнем случае, равна работе выхода А. Следовательно, соответствующая красной границе фотоэффекта частота равна
больше или, в крайнем случае, равна работе выхода А. Следовательно, соответствующая красной границе фотоэффекта частота равна  . Она зависит только от работы выхода электрона, т.е. от химической природы металла и состояния его поверхности.
. Она зависит только от работы выхода электрона, т.е. от химической природы металла и состояния его поверхности.
Фотоны.
Чтобы объяснить распределение энергии в спектре равновесного теплового излучения достаточно, как показал Планк, допустить, что свет испускается порциями 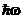 . Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Далее Эйнштейн выдвинул гипотезу, что свет распространяется в пространстве также в виде дискретных частиц - фотонов.
. Для объяснения фотоэффекта достаточно предположить, что свет поглощается такими же порциями. Далее Эйнштейн выдвинул гипотезу, что свет распространяется в пространстве также в виде дискретных частиц - фотонов.
Фотон как частица обладает особыми свойствами хотя бы потому, что он движется со скоростью света. Поэтому формулы классической механики к движению фотона неприменимы, и нужно пользоваться релятивистскими соотношениями. Помимо энергии ε = ћ ω фотон должен обладать массой и импульсом. Формула для массы фотона может быть получена из формулы, выражающей взаимосвязь массы и энергии в теории относительности и формулы энергии фотона
 (2.3)
(2.3)
Согласно теории относительности импульс и энергия частицы, движущейся со скоростью v, равны
 . (2.4)
. (2.4)
Но так как фотон движется со скоростью света, то знаменатель обращается в ноль, и получаем что p = ∞ и Е = ∞. Это означает, что никакое тело нельзя разогнать до скорости света. В случае фотона следует считать, что его масса покоя m0 = 0, т.е. в природе не существует покоящихся фотонов. Ясно, что приведенные формулы (2.4) оказываются непригодными, так как имеем неопределенности типа 0/0. Исключив из (2.4) скорость v , получим соотношение, связывающее импульс и энергию

Для фотона m0 =0 и Е= ε = ћ ω, отсюда
 . (2.5)
. (2.5)
Так как фотон обладает импульсом, то, встречая на пути какое-нибудь препятствие, поток фотонов должен оказывать на это препятствие давление, подобно тому, как молекулы газа оказывают давление на стенки сосуда. Впервые русский физик Лебедев экспериментально измерил световое давление и подтвердил существование импульса у фотонов. Однако следует заметить, что в своих исследованиях Лебедев руководствовался не корпускулярной теорией света, а электромагнитной теорией Максвелла, которая тоже приводит к выводу о существовании светового давления. Обе теории дают одну и ту же формулу для вычисления светового давления  - интенсивность света (n-количество фотонов, падающих на единицу поверхности в единицу времени), ρ – коэффициент отражения света от поверхности тела. Это объясняется тем, что связь между импульсом и энергией фотона идентична связи между энергией и импульсом электромагнитного поля p = E/c.
- интенсивность света (n-количество фотонов, падающих на единицу поверхности в единицу времени), ρ – коэффициент отражения света от поверхности тела. Это объясняется тем, что связь между импульсом и энергией фотона идентична связи между энергией и импульсом электромагнитного поля p = E/c.
Если ввести волновое число  , то выражение (2.4) можно переписать в форме
, то выражение (2.4) можно переписать в форме
 (2.6)
(2.6)
Направление импульса совпадает с направлением распространения света, характеризуемым волновым вектором k, численно равным волновому числу.
Таким образом, фотон подобно любой движущейся частице или телу, обладает энергией, массой и импульсом. Все эти три корпускулярные характеристики фотона связаны с волновыми его характеристиками – длиной волны или частотой. Корпускулярные свойства фотона не должны заставить нас забыть о том, что такие явления как дифракция и интерференция, могут быть объяснены только на основе волновых представлений.
Следовательно, свет обнаруживает корпускулярно-волновой дуализм (двойственность): в одних явлениях проявляется его волновая природа, и он ведет себя как электромагнитная волна; в других – проявляется корпускулярная природа света, и он ведет себя как поток фотонов.
Эффект Комптона.
Квантовые свойства света проявляются в эффекте, который обнаружил Комптон в 1923 г., наблюдая рассеяние монохроматического рентгеновского излучения. Схематически опыт Комптона можно изобразить следующим образом ( рис.1)
 ИРИ – источник рентгеновского излучения
ИРИ – источник рентгеновского излучения
D – фокусирующая диафрагма
РВ - рассеивающее вещество Рис.1
Θ - угол рассеивания
В опыте было установлено, что в рассеянных лучах наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ´. Разность  оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. С точки зрения классической волновой теории было невозможно объяснить эффект Комптона. Согласно этой теории, рассеяние света есть процесс переизлучения электромагнитных волн электронами. Электроны совершают вынужденные колебания под действием поля электромагнитной волны. Вынужденные колебания происходят на частоте вынуждающей силы. В результате в веществе должны возникать электромагнитные волны той же частоты (или длины волны).
оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. С точки зрения классической волновой теории было невозможно объяснить эффект Комптона. Согласно этой теории, рассеяние света есть процесс переизлучения электромагнитных волн электронами. Электроны совершают вынужденные колебания под действием поля электромагнитной волны. Вынужденные колебания происходят на частоте вынуждающей силы. В результате в веществе должны возникать электромагнитные волны той же частоты (или длины волны).
С квантовой точки зрения рассеяние можно рассматривать как процесс упругого соударения рентгеновских фотонов с практически свободными электронами. Свободными можно считать внешние электроны, энергия связи которых в атоме значительно меньше той энергии, которую фотон может передать электрону при соударении.
Пусть на покоящийся электрон падает фотон с энергией ħω и импульсом ħk( Рис.2)
Энергия электрона до столкновения 
Энергия электрона после столкновения 
 Импульс электрона до столкновения p = 0.
Импульс электрона до столкновения p = 0.
Импульс электрона после столкновения

Энергия фотона до столкновения 
Энергия фотона после столкновения 
Импульс фотона до столкновения  Рис.2
Рис.2
Импульс фотона после столкновения 
Закон сохранения энергии и импульса
 (*)
(*)
Перепишем первое уравнение в виде
 ,
,
или  (**)
(**)
Решая систему уравнений (*), с учетом преобразований (**) получим

или
 ,
,
где  - комптоновская длина волны (в данном случае, электрона).В эффекте Комптона рентгеновский фотон проявляет корпускулярные свойства.
- комптоновская длина волны (в данном случае, электрона).В эффекте Комптона рентгеновский фотон проявляет корпускулярные свойства.
Вопросы для самоконтроля:
1. Как изменится фототок насыщения с уменьшением освещенности при данной частоте?
2. Как будет уменьшаться максимальная кинетическая энергия фотоэлектрона при увеличении частоты падающего излучения? От его интенсивности?
3. Нарисуйте вольт-амперные характеристики соответствующим двум различным частотам (при заданной освещенности).
4. Нарисуйте вольт-амперные характеристики соответствующим двум различным освещенностям (при заданной частоте).
5. Найдите отношение давлений света на зеркальную и черную поверхности.
6. В чем отличие характера взаимодействия при эффекте Комптона и фотоэффекте?
7. В каких случаях свет проявляет корпускулярную, а в каких волновую природу?
Лекция № 3.
СТРОЕНИЕ АТОМА.
План
1. Явления, подтверждающие сложное строение атома.
2. Спектральные закономерности.
3. Модель атома Резерфорда.
4. Постулаты Бора.
5. Атом водорода.
1. Явления, подтверждающие сложное строение атома.
Первоначально высказанная в виде догадки идея об атомном строении вещества по мере развития науки подтверждалась все большим числом опытов и в XIX веке превратилась в общепризнанную теорию. Вплоть до конца XIX века атомы считались вечными неизменными и неделимыми частицами материи, не имеющими внутренней структуры. Однако во второй половине XIX века было обнаружено много таких явлений, которые ставили под сомнение предположение об отсутствии внутренней структуры у атомов. Перечислим основные:
1. Электризация – электрические заряды, как положительные, так и отрицательные, должны входить в состав атомов.
2. Исследование оптических спектров химических элементов – атомы каждого химического элемента дают свое собственное излучение. Из электромагнитной теории света следует, что излучение атомов имеет электромагнитную природу, т.е. должно создаваться тем или иным движением зарядов, входящих в состав атома.
3. Открытая Менделеевым в 1869 г. периодичность свойств химических элементов свидетельствовала о повторяющихся комбинациях электрических зарядов внутри атомов.
4. Законы электролиза, установленные Фарадеем.
5. При опытах с рентгеновскими лучами и по фотоэффекту были обнаружены отрицательные и абсолютно одинаковые частицы, названные в 1891 г. электронами.
6. Открытие Беккерелем в 1896 г. излучения, источником которого являлись урановые руды и природа которого была не ясна. Последующие исследования П. и М. Кюри, Резерфорда показали, что это излучение имеет сложный характер и может быть разделено на лучи трех видов - α, β, γ. α – лучи оказались состоящими из дважды ионизированных атомов гелия, получивших название α-частиц, β-лучи - потоком быстрых электронов (β-частицы), γ-лучи - очень короткими электромагнитными волнами.
