Геометрический и физический смысл определенного интеграла

1. Путь S, пройденный точкой по прямой за время T – t₀ со скоростью v=v(t) (v(t) непрерывна на [t₀; T]), есть .

2. Если переменная сила F=f(x) действует в направлении оси Ox (f(x) – непрерывна на [a; b]), то работа этой силы на отрезке [a; b] оси Ох равна .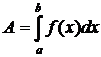

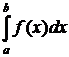3. Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), снизу – отрезком [a; b] оси Ох, с боков – отрезками прямых x=a, x=b.

Пример 3.5.11.Найти площадь фигуры, ограниченной параболой и гиперболой .

○ Найдем точки пересечения параболы и гиперболы, для этого решим систему уравнений:

;

;

;

, ; , .

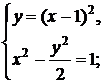
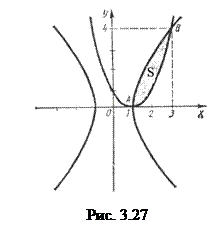
Таким образом, заданные кривые пересекаются в точках А(1; 0) и В(3; 4) (рис. 3.27). Следовательно,

4,58 (кв. ед.). ●

Замена переменной в определенном интеграле

Формула замены переменной в определенном интеграле:

,

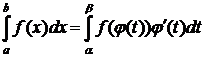где 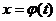, α и β определяются из условий 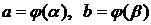соответственно.

Пример 3.5.12. Вычислить .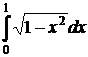

○

●

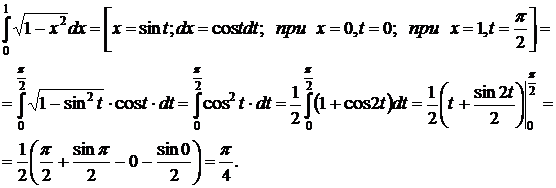
Теорема 3.5.6. (Теорема о среднем)Если функция f(x) непрерывна на отрезке [a; b], то в интервале (a; b) найдется такая точка с, что

.

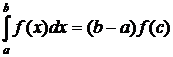Интегрирование по частям в определенном интеграле

Пусть u=u(x), v=v(x) – непрерывно дифференцируемые на отрезке [a; b] функции. Тогда

.

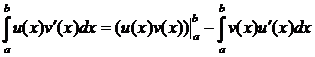Определенный интеграл с переменным верхним пределом

Пусть функция f(x) непрерывна на отрезке [a; b]. Рассмотрим интеграл

,

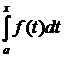где х – любая точка из [a; b].

Если F(x) – первообразная функции f(x), т.е. F′(x)=f(x), то согласно формуле Ньютона-Лейбница имеем:

.

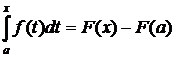Отсюда

.

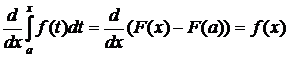Таким образом, производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции от этого предела.

Несобственные интегралы

Интегралы с одним или обоими бесконечными пределами получили название несобственных интегралов первого рода. Здесь также, как при вычислении определенных интегралов, можно на практике использовать формулу Ньютона-Лейбница, однако следует помнить, что символ ∞ – не число, а условное обозначение неограниченного возрастания (или убывания) аргумента в процессе его изменения. То есть, со строгих позиций, вычисление несобственного интеграла первого рода – это вычисление некоторого предела, с постоянным использованием теорем о бесконечно малых и бесконечно больших величинах.

Таким образом:

;

;

.

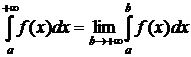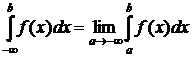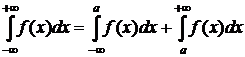То есть, символы бесконечности условно заменяются буквенными параметрами, применяется формула Ньютона-Лейбница, после чего обычным образом вычисляются указанные пределы. Если в результате такого расчета получится конечное число А (включая 0), то ответ следует записать в форме: интеграл сходится к значению А. Если же результатом будет +∞ (или –∞) или предел не существует, то ответ: интеграл расходится.

В практических вычислениях, вполне допустимо не использовать в явной форме операторы lim, но не следует забывать о том, что на самом деле вычисляются пределы, а не конкретные числовые значения.

Следующим видом несобственных интегралов являются интегралы от функций с разрывом на одном конце (или обоих концах) интервала интегрирования или с разрывом внутри интервала интегрирования. Например: 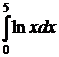, 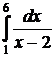и т.п. Такие интегралы носят название несобственных интегралов второго рода. Эти интегралы очень опасны, т.к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.

Вычисление несобственных интегралов второго рода осуществляется приведением к интегралам первого рода (или сумме таких интегралов), то есть, ставится задача вычисления предела относительно точки, в которой подынтегральная функция разрывна.