Расчет линий равного потенциала
Уравнением линии равного потенциала является уравнение окружности с радиусом:
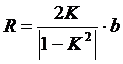 .
.
И координатами центра окружности
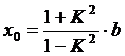 ;
; 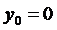 ;
;
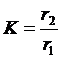 .
.
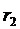 - расстояние от электрической оси, расположенной справа от оси OY до произвольной точки на линии равного потенциала;
- расстояние от электрической оси, расположенной справа от оси OY до произвольной точки на линии равного потенциала;
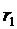 - то же для оси слева от OY .
- то же для оси слева от OY .
Таким образом, если найдено К, то для каждой линии равного потенциала могут быть вычислены 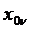 и радиус
и радиус 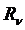 ,
,
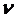 - порядковый номер линии.
- порядковый номер линии.
Расчёт 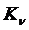 производится следующим образом, пусть Uo заданная разность потенциала между электрическими осями, тогда:
производится следующим образом, пусть Uo заданная разность потенциала между электрическими осями, тогда:
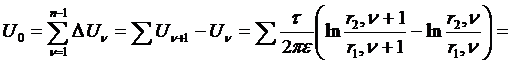
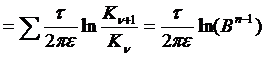
где 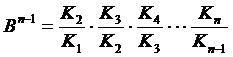 ;
;

При условии, что ΔU = const, имеем В = const, т.е. число К при возрастании порядкового номера линий изменяются в геометрической прогрессии:
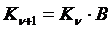
В нашем случае:
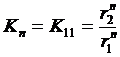 ;
; 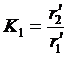
Если счет линий выполнять слева направо, из рис.1 следует:
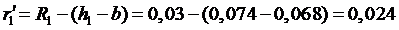 м;
м;
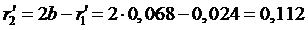 м;
м;
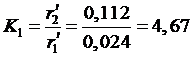 ;
;
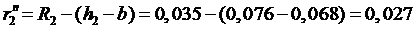 м;
м;
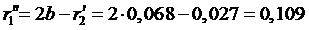 м;
м;
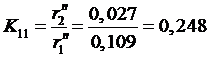 .
.
Определим В, имея ввиду, что по условию n-1=10
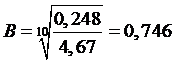 .
.
Дальнейший расчет, связанный с определением радиусов и координат центра эквивалентных окружностей, сводим в таблицу.
Таблица 1.1 Расчет линий равного потенциала
 | 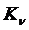 | 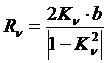 (м) (м) |  (м) (м) |
| 4,67 | 0,03 | -0,075 | |
| 3,48 | 0,043 | -0,08 | |
| 2,6 | 0,061 | -0,092 | |
| 1,94 | 0,096 | -0,117 | |
| 1,45 | 0,18 | -0,193 | |
| 1,08 | 0,89 | -0,896 | |
| 0,805 | 0,311 | 0,318 | |
| 0,6 | 0,128 | 0,145 | |
| 0,45 | 0,076 | 0,102 | |
| 0,334 | 0,051 | 0,085 | |
| 0,248 | 0,035 | 0,077 |
Радиусы первой и последней линии равны радиусам цилиндров.
Построение линий равного потенциала
По данным таблицы 1 и с учетом результатов расчета по пункту 1.1 производится построение линий равного потенциала. Построение производится на миллиметровой бумаге формата А3 (297*420 мм) для первой схемы в масштабе 1:1, для второй в масштабе 1:2. На чертеже должны быть нанесены все основные величины, полученные при расчете.
Расчет линий напряжённости Е поля
Уравнение любой линии Е поля является уравнением дуги окружности, пересекающейся с электрическими осями с координатами центра:
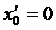 ;
; 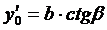 ,
,
где β – угол между линиями соединяющими точку пересечения κ-той линии напряженности Е с плоскостью нулевого потенциала с электрическими центрами цилиндров.
Линии Е поля должны быть построены так, чтобы весь поток Е был поделён ими на равное целое число трубок. Для этого, при переходе от любой линии Е к соседней необходимо изменить угол β на постоянную величину 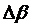 .
.
Вычисление 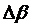 :
:
За начальную линию Е принимают линию, соединяющую электрические оси. Угол для неё равен: 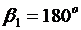 .
.
Вторую линию строят (от руки) таким образом, чтобы в результате пересечения обеих линий с эквипотенциальной линией получался квадрат.
Соединяя любую точку отрезка второй линии, являющегося верхней стороной квадрата, с электрическими осями находят угол β2 и вычисляют 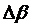 :
:
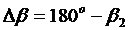
Поскольку диапазон изменения 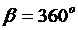 , то число линий Е поля:
, то число линий Е поля:
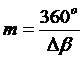
Полученный результат округляется до ближайшего целого чётного 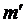 .
.
После этого уточняется 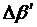 :
:
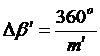 ;
; 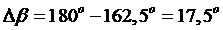 ;
; 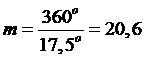 .
.
Округляем до ближайшего чётного числа 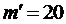 ;
; 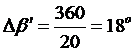
Расчет координат 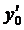 сведен в таблицу 1.2.
сведен в таблицу 1.2.
Таблица 1.2 Расчет линий напряженности поля
| κ | 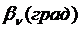 | 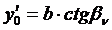 , (м) , (м) | 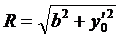 , (м) , (м) |
| ∞ | ∞ | ||
| 0,209 | 0,22 | ||
| 0,094 | 0,116 | ||
| 0,049 | 0,084 | ||
| 0,022 | 0,071 | ||
| 0,068 | |||
| -0,022 | 0,071 | ||
| -0,049 | 0,084 | ||
| -0,094 | 0,116 | ||
| -0,209 | 0,22 | ||
| ∞ | ∞ |
Начиная с 1800 значения 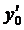 будут повторяться по величине и знаку.
будут повторяться по величине и знаку.
