Стационарное уравнение Шредингера.

Стационарное уравнение Шредингера для электрона в водородопо-добном ионе

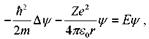
где: Z - зарядовое число

(Z = 1 для водорода, Z = 2 для He⁺ , Z = 2 для Li⁺⁺), m = 9,11·10^–31 кг - масса электрона, е = 1,6·10^–19 Кл - заряд электрона, ε ₀ = 8,85·10 ¹² Ф/м - электрическая постоянная, h = 1,056·10-³⁴ Дж·с - постоянная Планка, r - расстояние от ядра до электрона, Е - энергия электрона,

- волновая функция, зависящая только от координат.

Так как поле, в котором движется электрон, является центрально-симметричным, то для решения данного уравнения обычно используют сферическую систему координат

В теории дифференциальных уравнений показано, что уравнение

имеет решения, удовлетворяющиетребованиям однозначности, конеч-ности и непрерывности волновой функции ψ, только при собственных значениях энергии

где n = 1, 2, 3, … - главноеквантовое число.

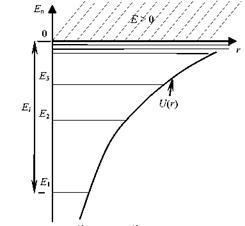
Таким образом, решение уравнения Шредингера для атома водоро-да (Z = 1) приводит к появлению дискретных энергетических уровней E₁, E₂, E₃, … , показанных на рисунке в виде горизонтальных прямых.

Состояниес наименьшей энергией является основным

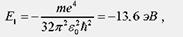все остальные состоянияназываются возбуждённые.

По мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = ∞ энергия E_∞ = 0. При E > 0 движение электрона является свободным.

Энергия ионизации атома водорода

Из решения уравнения Шредингера вытекает, что момент импуль­са электрона не может быть произвольным, а принимает дискретные значения

где l - орбитальное квантовое число, которое при заданном n принима­ет значения l = 0, 1, 2, …, (n - 1), т.е. всего n значений.

Из решения уравнения Шредингера следует также, что вектор мо­мента импульса электрона может иметь лишь такие ориентации в про­странстве, при которых его проекция на направление oz внешнего маг­нитного поля принимает квантованные значения, кратные h

где ml - магнитное орбитальноеквантовое число, которое при задан­ном l может принимать значения m_l = 0,±1,±2,...,± l., т.е. всего 2l + 1

значений.

Спинэлектрона - это собственный механический момент импуль­са электрона, не связанный с движением электрона в пространстве.

Спин электрона (и всех других микрочастиц) - квантовая величина, у неё нет классического аналога; это внутреннее неотъемлемое свойст­во электрона, подобное его заряду и массе.

Собственный механический момент импульса (спин) Ls согласно общим выводам квантовой механики квантуется по закону

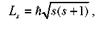где s =1\2 спиновое квантовое число.

Проекция спина на направление внешнего магнитного поля при­нимает квантованные значения,кратные h

где m_s - магнитное спиновое квантовое число, которое имеет только два

значения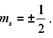

Хотя энергия электрона и зависит только от главного квантового числа n, но каждому собственному значению энергии E _n (кроме E ₁) со­ответствует несколько собственных функций отличаю­щихся значениями квантовых чисел l, ml и m_s Следовательно, атом во­дорода может иметь одно и тоже значение энергии, находясь в несколь­ких различных состояниях, соответствующих данному n.