Прямолинейный проводник с током

Линии магнитной индукции представляют собой концентрические окружности с центром на проводнике

Круговой ток

Направление вектора магнитной индукции связано с направлением ток в контуре правилом правого винта

Постоянный магнит — изделие различной формы из магнитотвёрдого материала с высокой остаточной магнитной индукцией, сохраняющее состояние намагниченности в течение длительного времени. Постоянные магниты применяются в качестве автономных (не потребляющих энергии) источников магнитного поля.

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 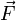магнитное поле действует на заряд 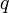, движущийся со скоростью 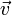, т.е. действие магнита на объект без механического вмешательства.

43.При помещении провода с током в магнитное поле действующая на носители тока магнитная сила передается проводу. Получим выражение для магнитной силы, действующей на элементарный отрезок провода длиной dl в магнитном поле с индукцией В.

Обозначим заряд одного носителя q₁, концентрацию носителей n , скорость упорядоченного движения носителей u , скорость хаотического движения v. Магнитная сила, действующая на один носитель

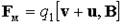, (4.2.1)

Ее среднее значение равно

.

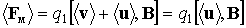Здесь 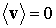, так как все направления скорости хаотического движения равновероятны.

Пусть площадь сечения провода S , тогда объем отрезка провода равен Sdl и общее число носителей nSdl. Суммарная магнитная сила, действующая на элементарный отрезок провода, равна

.

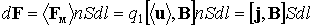Здесь 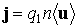плотность тока.

Величина плотности тока j связана с силой тока I и площадью сечения S: j=I/S . Введем вектор элемента длины проводника dl , сонаправленный с вектором плотности тока j, тогда jSdl=Idl и для магнитной силы, действующей на элемент тока, получаем

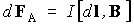. (4.2.2)

Это соотношение было получено экспериментально Ампером и называется законом Ампера. Исторически оно было получено раньше, чем выражение для магнитной части силы Лоренца. В действительности, Лоренц получил выражение для магнитной силы, основываясь на законе Ампера.

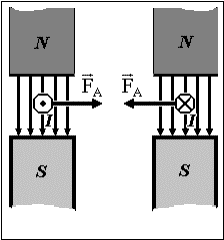
Для прямого отрезка провода с током I, помещенного в однородное магнитное поле B, сила Ампера равна

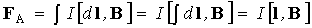. (4.2.3)

Здесь вектор l направлен по току (в сторону переноса положительного заряда), а его модуль равен длине провода. Направление амперовой силы определяется так же, как направление магнитной силы для положительного заряда (см. рис. 4.2.3).

Элементарная работа dА, совершаемая силой Ампера dF_А при перемещении на dr в магнитном поле элемента проводника dl, равна

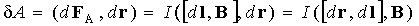. (4.2.4)

Здесь мы, подставив выражение для амперовой силы (4.2.2), вынесли скалярную величину – силу тока I и воспользовались известным свойством смешанного произведения векторов: оно не изменяется при циклической перестановке сомножителей. Векторное произведение перемещения и элемента проводника есть вектор площадки, прочерченной проводником при его перемещении (см. рис. 4.2.4):

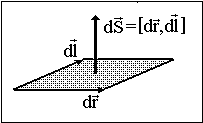
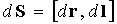. (4.2.5)