Векторные диаграммы для представления гармонических колебаний.

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.

Гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса).

Гармонические колебания описываются уравнением типа:

x =A cos (₀ t +) ,

где

x – смещение колеблющейся точки от положения равновесия.

А - максимальное значение колеблющейся величины, называемое амплитудой колебания,

0 - круговая (циклическая) частота,

 -начальная фаза колебания в момент времени t=0,

(₀ t +) - фаза колебания в момент времени t.

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.

Для этого из произвольной точки О, выбранной на оси x под углом ,равнымначальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания.

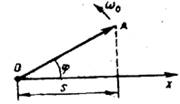
Если этот вектор привести во вращение с угловой скоростью ₀, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от -А до +А , а колеблющаяся величина будет изменяться со временем по закону s =A cos (₀ t +). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом , равным начальной фазе, и вращающегося с угловой скоростью ₀ вокруг этой точки.

Дифференциальное уравнение гармонических колебаний материальной точки.

, или , где m – масса точки, k – коэффициент квазиупругой силы (k=mw²).

Решение:

кинематическое уравнение гармонических колебаний

Энергия колебательного движения.

Динамика гармонических колебаний:

Пружинный и физический маятники.

Пружинный маятник

Колебательная система в этом случае представляет собой совокупность некоторого тела и прикрепленной к нему пружины. Пружина может располагаться либо вертикально (вертикальный пружинный маятник), либо горизонтально (горизонтальный пружинный маятник).

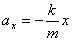
где а_х – ускорение, m - масса, х - смещение пружины, k – жесткость пружины.

Это уравнение называют уравнением свободных колебаний пружинного маятника. Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)силы трения, действующие на тело, пренебрежимо малы и поэтому их можно не учитывать;

2) деформации пружины в процессе колебаний тела невелики, так что можно их считать упругими и в соответствии с этим пользоваться законом Гука.

Закон Гука, устанавливает линейную зависимость между упругой деформацией твердого тела и приложенным механическим напряжением. Напр., если стержень длиной l и поперечным сечением S растянут продольной силой F, то его удлинение = Fl/ ES, где E — модуль упругости (модуль Юнга).