Метод расчета дифракции рентгеновских лучей.формула Вульфа-Брэгга

Если поставить две дифракционные решетки одна за другой так, чтобы их щели были перпендикулярны, то первая решетка дает ряд максимумов, положение которых определяется условием

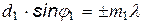
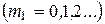
Вторая решетка разобьет каждый из образовавшихся пучков на расположенные максимумы, перпендикулярные максимумам от первой решетки и удовлетворяющие условию:

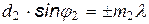
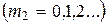
Даваемая таким образом картина будет представлять вид правильно расположенных пятен, каждое из которых будет удовлетворять указанным условиям и и каждому будет соответствовать пара чисел m₁, m₂. (Та же картина получится, если разделить пластинку на систему взаимно перпендикулярных штрихов.Такая пластина называется двумерной периодической структурой).

Дифракция наблюдается и на трехмерных структурах, обнаруживающим периодичность по трем пространственным направлениям. К таким структурам относятся кристаллические тела. Однако для видимого света 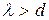( 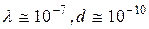), так как период кристаллической решетки 10^-10м. Условие 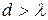будет выполняться для рентгеновских лучей. В 1913 году Лауэ, Фридрих обнаружили дифракцию на рентгеновских лучах. Русский ученый Вульф и английский Брегги независимо друг от друга предложили простой метод расчета дифракционной картины от кристаллической решетки. Этот метод основан на интерференции отраженных от атомных слоев плоских вторичных волн, которые будут усиливать друг друга в определенных направлениях, определяемых условием

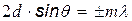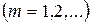, - формула Вульфа-Бреггов

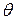- угол скольжения

d – период идентичности кристалла в направлении, перпендикулярном слоям.

Получается на фотопластине картина в виде точек, взаимное расположение которых отражает симметрию кристалла. По расстоянию между пятнышками и интенсивности определяют расположение атомов.

По дифракционной картине от различно направленных в кристалле атомным слоям можно выяснить кристаллическую структуру. Атомные слои, густо населенные атомами, дают более интенсивные максимумы.

Дифракция рентгеновских лучей на кристаллах используется:

1. Для определения спектрального состава рентгеновских лучей на кристаллах с известной кристаллической структурой (рентгеновская спектроскопия)

2. Для рентгеноструктурного анализа (определения структуры кристаллов)

Понятие о голографии

Голография – переводится «полна запись» - это система методов записи и воспроизведения структуры световой волны, отраженной предметом на фотопластинке. При освещении голограммы пучком света зафиксированная на ней волна восстанавливается почти в первоначальном виде (зрительное впечатление такое же, как и от реального предмета).

Идея голографии принадлежит Габоргу (1947 г). Первая голограмма была получена в 1963 году американцами Лейтом и Упатнисксом. Денисюк предложил метод, позволяющий на толстослойной эмульсии зафиксировать цветную голограмму.

Основное требование при голографии – высокая когерентность световых лучей, которая достигается при использовании лазерных лучей. На тонкослойной эмульсии получение голограмм заключается в разделении расширенного лазерного пучка с помощью линз на две части: одна часть, отразившись от зеркала 3 образует опорный пучок 1, падающий на фотопластинку, другая часть образует предметный пучок 2, отразившись от предмета. Их интерференционная картина фиксируется фотопластиной. После восстановления голограмма освещается опорным пучком 1, который дифрагирует на голограмме, создавая световую волну, с такой же структурой, как и отраженный от предмета, и создает мнимое изображение. (Оно является объемным, нужно по разному аккумулировать глаз). Действительное изображение псевдоскопично.

Применение: голографическое кино, телевидение, микроскоп, контроль качества обработки изделий.

5. Дисперсия света

Явление зависимости показателя преломления вещества от длины волны называют дисперсией света

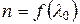
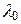- длина световой волны в вакууме.

Дисперсией вещества называют производную n по 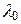: D = .

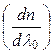Для всех прозрачных сред для видимого света с увеличением длины волны 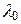показатель преломления n уменьшается, откуда следует

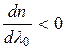
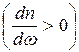(5.0)

Это нормальная дисперсия.

Если 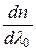>0, то дисперсия является аномальной. Среды, в которых скорость световой волны зависит от 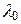, называются диспергирующими.

Формула Вульфа — Брэггов2dsinq=ml (m=1, 2, 3, ...),

38.дифракционная решетка как спектральный аппарат.критерии Рэлея

Дифракционная решетка является важнейшим спектральным прибором, предназначенным для разложения света в спектр и измерения длин волн. Из формулы (3.9.4), определяющей направления на главные фраунгоферовы максимумы, видно, что эти направления 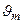зависят от длины световой волны l (за исключением максимума нулевого порядка, m = 0). Поэтому решетка в каждом порядке m ¹ 0 разложит падающий на нее свет в спектр различных порядков. Причем наибольшее отклонение в каждом порядке испытывает красная часть спектра (более длинноволновая).

Основными характеристиками любого спектрального прибора являются угловая дисперсия, разрешающая способность и область дисперсии.

1.Угловая дисперсия D характеризует степень пространственного (углового) разделения волн с различными длинами l. По определению,

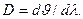(3.9.10)

где 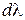- разность длин волн, дающих максимум данного порядка, 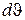- разность углов под которыми эти максимумы наблюдаются.

Дифференцируя формулу (3.9.4) при данном m находим для решетки 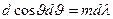, откуда

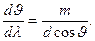(3.9.11)

Видно, что для заданного порядка m спектра угловая дисперсия тем больше, чем меньше период d решетки. Кроме того, 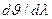растет с увеличением угла дифракции .

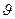2. Разрешающая способность R. По определению,

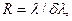(3.9.12)

где 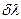— наименьшая разность длин волн спектральных линий, при которой эти линии воспринимаются еще раздельно, т. е. разрешаются. Величина R не может быть по ряду причин определена точно, а лишь ориентировочно (условно). Такой условный критерий был предложен Рэлеем.

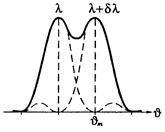
Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, Рис.3.9.8.

считаются разрешенными, если главный максимум одной спектральной линии совпадает с первым минимумом другой (рис.3.9.8). В этом случае между двумя максимумами возникает провал, составляющий около 20% от интенсивности в максимумах, и линии еще воспринимаются раздельно.

Итак, согласно критерию Рэлея и формуле (3.9.9), необходимо, чтобы максимум m-го порядка (m’ = mN) линии с длиной волны l + dl (рис.3.9.8) совпадал по направлению с первым минимумом линии l (m’ = mN + 1), т. е.

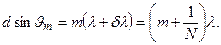
Отсюда следует, что

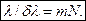(3.9.13)

Критерии Рэлея - два близлежащих одинаковых точеч­ных источника или две близлежащие спектральные линии с равными интенсивностями условно считаются полностью разрешенными (наблюдаемыми порознь), если максимум интенсивности одного источ­ника (линии) совпадает с первым миниму­мом интенсивности другого