Опытные законы идеального газа.

Закон Бойля—Мариотта*: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: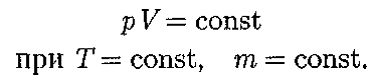

Законы Гей-Люссака*:1) объем данной массы газа при постоянном давлении изменяется линейно с температурой: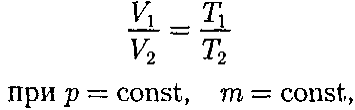

2) давление данной массы газа при постоянном объеме изменяется линейно с тем­пературой:

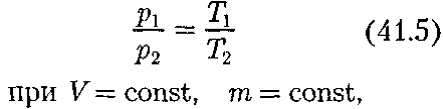
Закон Авогадро*: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41×10^–3 м³/моль.

По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:

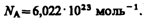
Закон Дальтона*: давление смеси идеальных газов равно сумме парциальных давлений p₁, p₂,..., р_n входящих в нее газов:

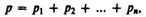
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.

Уравнение Клайперона - Менделеева.

Уравнению

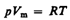(42.4)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева.

Уравнение Клапейрона — Менделеева для массы т газа

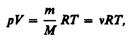(42.5)

где n =m/M — количество вещества

Основное уравнение МКТ идеального газа.

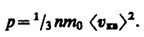(43.3)

Выражение (43.3) называетсяосновным уравнением молекулярно-кинетической те­ории идеальных газов.

Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения.

Применяя методы теории вероятностей, Максвелл нашел функцию f(v) —закон распределения молекул идеального газа по скоростям:

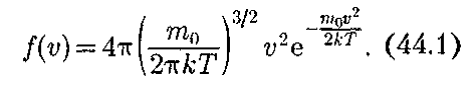
функция распределения молекул по энергиям теплового движения

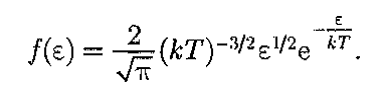
Барометрическая формула

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Выражение (45.2) называется барометрической формулой

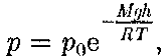
40. Среднее число столкновений и средняя длина свободного пробега молекул

средняя длина свободного пробега молекул (l)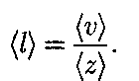

Таким образом, среднее число столкновений Расчеты показывают, что при учете движения других молекул

Тогда средняя длина свободного пробега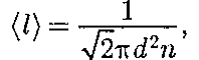

41. Опытное обоснование МКТ

1. Броуновское движение. Шотландский ботаник Р. Броун (1773—1858), наблюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что частицы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что подобное сложное зигзагообразное движение характерно для любых частиц малых размеров (1 мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды, с уменьшением вязкости и размеров частиц (независимо от их химической природы). Причина броуновского движения долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффекта ему было дано объяснение: броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены. Так как молекулы движутся хаотически, то броуновские частицы получают толчки с разных сторон, поэтому и совершают движение столь причудливой формы. Таким образом, броуновское движение является подтверждением выводов молекулярно-кинетической теории о хаотическом (тепловом) движении атомов и молекул.

2. Опыт Штерна. Первое экспериментальное определение скоростей молекул выполнено немецким физиком О. Штерном (1888—1970). Его опыты позволили также оценить распределение молекул по скоростям. Схема установки Штерна представлена на рис. 70. Вдоль оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О. Если прибор привести во вращение вокруг общей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние s. Изображение щели получается размытым. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.

Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя s, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Результаты опыта показали, что средняя скорость атомов серебра близка к той, которая следует из максвелловского распределения молекул по скоростям.

3. Опыт Ламмерта. Этот опыт позволяет более точно определить закон распределения молекул по скоростям. Схема вакуумной установки приведена на рис. 71. Молекулярный пучок, сформированный источником, проходя через щель, попадает в приемник. Между источником и приемником помещают два диска с прорезями, закрепленных на общей оси. При неподвижных дисках молекулы достигают приемника, проходя через прорези в обоих дисках. Если ось привести во вращение, то приемника достигнут только те прошедшие прорезь в первом диске молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска. Другие же молекулы задерживаются вторым диском. Меняя угловую скорость вращения дисков и измеряя число молекул, попадающих в приемник, можно выявить закон распределения молекул по скоростям. Этот опыт также подтвердил справедливость максвелловского распределения молекул по скоростям.

4. Опытное определение постоянной Авогадро. Воспользовавшись идеей распределения молекул по высоте (см. формулу (45.4)), французский ученый Ж. Перрен (1870—1942) экспериментально определил значение постоянной Авогадро. Исследуя под микроскопом броуновское движение, он убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцмановское распределение, можно записать

где т—масса частицы, т1—масса вытесненной ею жидкости; m=4/3r3, m1=4/3r31 (r — радиус частицы,  — плотность частицы, 1 — плотность жидкости).

Если n1 и n2 — концентрации частиц на уровнях h1 и n2, a k=R/NA, то

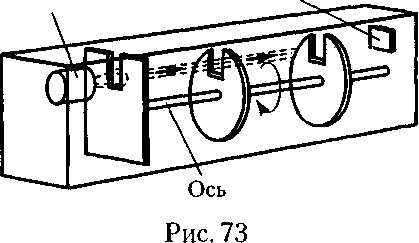
Значение NA, получаемое из работ Ж. Перрена, соответствовало значениям, полученным в других опытах, что подтверждает применимость к броуновским частицам распределения (45.4).

42. Явления переноса в термодинамически неравновесных системах.

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса.

Явление, обусловленные переносом энергии, называется теплопроводностью.

Явление, обусловленное переносом массы, называется диффузией.

Явление, обусловленное переносом импульса, называется внутренним трением.

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени, вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, процесс выравнивания температур.

Теплопроводность λ численно равна плотности теплового потока при градиенте температуры равном единице.

Можно показать, что:

(47.2)

где

c_V – удельная теплоёмкость при постоянном объёме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объёме);

ρ- плотность газа;

<v> - средняя скорость теплового движения молекул;

<l> - средняя длина свободного пробега.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твёрдых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности.

Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.

Согласно кинетической теории газов:

D=(1/3)<υ><l>

(47.4)

Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Динамическая вязкость η числено равна плотности потока импульса при градиенте скорости, равном единице.

Её можно вычислить по формуле:

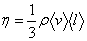(47.7)

Из сопоставления формул (47.2), (47.4) и (47.7), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти зависимости были установлены задолго до выводов молекулярно-кинетической теории. Из этих формул вытекают простые зависимости между η, D, λ:

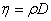(47.8)

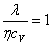(47.9)

Используя эти формулы, можно по найденным из опыта одним величинам определить другие.