Потенциальный барьер. Туннельный эффект

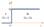
Потенциальный барьер – область пространства, в которой находится максимум потенциальной энергии частицы. Рассмотрим потенциальный барьер прямоугольной формы, шириной l и высотой U0 (РИС. 39.1).

Рассмотрим сначала бесконечный барьер (l → ∞).

Пусть на него налетает (из области I) частица массы m с энергией W < U0. Запишем стационарное уравнение Шрёдингера в виде (38.7 ) . (Задача одномерная, поэтому .)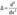

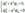Область I : 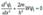Обозначим

Область II : Обозначим

Получим систему дифференциальных уравнений

Ищем решение каждого из этих уравнений в общем виде ψ = e^λx. Тогда ψˊ = λe^λx, ψˊˊ = λ2e^λx;

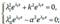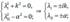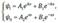® ® (39.1)

Здесь i – мнимая единица, A1, B1, A2, B2 – постоянные.

Коэффициент A1 характеризует набегающую волну (налетающую частицу), B1 – отражённую волну (отлетающую от барьера частицу), A2 и B2 характеризуют вероятность нахождения частицы внутри барьера. Так как эта вероятность не может расти при погружении вглубь барьера, A2 = 0.

Найдём коэффициенты A2 и B1. Условие непрерывности волновой функции награнице барьера:

(39.2)

Условие непрерывности производных волновой функции: (39.3)

Из (39.2) и (39.3) получим (39.4)

Вероятность нахождения частицы в точке с координатой x = 0 определяется выражением

Вероятность (плотность вероятности) нахождения частицывнутри барьера на расстоянии x от его границы

Теперь «обрежем» барьер на ширине x = l. Прозрачность барьера – вероятность прохождения барьера частицей:

Подставим сюда функции (39.1). С учётом (39.4) получим

В..большинстве..реальных..задач Тогда ,

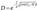
Мы доказали, что даже имея энергию, меньшую, чем высота потенциального барьера, частица может преодолеть этот барьер. В этот состоит Туннельный эффект.

9)Квантовомеханическая модель атома водорода. Уравнение Шрёдингера и его решение для основного состояния.

Атом состоит из положительно заряженного ядра, окружённого облаком электронов. Для атома водорода масса протона mp намного больше массы электронаme. поэтому ядро можно считать неподвижным.

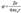
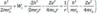Потенциал электростатического поля ядра
где Z – заряд ядра (число протонов в ядре), r – расстояние от ядра до электрона.
Потенциальная энергия электрона в этом поле
Стационарное уравнение Шрёдингера

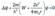
где m – масса электрона (данное обозначение используется в этом и следующем разделах).
Так как поле – центральное, перейдём к сферической системе координат. Стационарное уравнение Шрёдингера запишется в виде
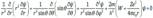(39.5)
Предположим, что существует такое симметричное состояние, в котором ψ = ψ₁(r),
с энергией W₁. Тогда 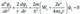. (39.6)
Будем искать решение этого уравнения в виде . Производные этой функции

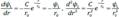
Подставим эти выражения в уравнение (39.6):

Домножив это уравнение на, получим ----------------------------(ψ1 ≠ 0).

Это равенство должно выполняться при любых r, в т. ч. при r → ∞. В таком случае
правая часть этого равенства стремится к нулю, а, следовательно, и левая часть
должна быть также равна нулю:

При r ≠ 0 должны выполняться равенства Из этой системы уравнений получим