Тема 6. интегральное исчисление функции одной переменной
ТЕМА 6. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1.Первообразная функция.
2.Понятие неопределенного интеграла и его свойства.
3.Таблица основных интегралов.
4.Методы интегрирования.
Одной из основных задач дифференциального исчисления является отыскание производной или дифференциала заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике, химии и технике приводят к обратной задаче: по заданной функции f(x) найти такую функцию F(x), производная которой была бы равна функции f(x), т.е. F′(x) = f(x).
Операция восстановления функции по известной производной этой функции называется интегрированием, а раздел математики, изучающий способы нахождения функции по ее производной и приложения этой операции, называется интегральным исчислением.
Вопрос 1. Первообразная функция
Одним из основных понятий интегрального исчисления является понятие первообразной.
О.1.1.Функция F(x) называется первообразной для функции f(x) на промежутке Х, если для всех хÎХ выполняется равенство
F′(x) = f(x).
Т.1.1. Если функция f(x) непрерывна на промежутке Х, то для нее на этом промежутке существует первообразная.
Пример.
Для функции f(x) = х2, хÎR, первообразной является функция  , так как
, так как  . Очевидно, что первообразными будут так же любые функции вида
. Очевидно, что первообразными будут так же любые функции вида  , где С – постоянная, т.к.
, где С – постоянная, т.к.  .
.
Т.1.2. (о множестве всех первообразных)
Пусть функция F(x) является первообразной для функции f(x) на промежутке Х. Тогда на данном промежутке функция f(x) имеет бесконечное множество первообразных, и все эти первообразные имеют вид F(x) + С, где С – произвольная постоянная.
Из теоремы 1.2 следует, что если известна какая-нибудь первообразная F(x) для данной функции f(x), то все множество первообразных для f(x) исчерпывается функциями вида F(x) + С.
Вопрос 2. Понятие неопределенного интеграла и его свойства
О.2.1. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных данной функции, т.е. множество функций вида F(x) + С.
Обозначение: òf(x)dx.
По определению òf(x)dx = F(x) + С.
В данном равенстве: F(x) - первообразная, C - произвольная постоянная, f(x) - подынтегральная функции, f(x)dx - подынтегральное выражение, ò - знак интеграла, х- переменная интегрирования.
О.2.2. Операция нахождения неопределенного интеграла от данной функции называется интегрированием, а раздел математики, изучающий интегрирование, называется интегральным исчислением.
Вопрос 3. Таблица основных интегралов
Приведем таблицу основных интегралов. Часть формул следует непосредственно из определения интегрирования, как операции, обратной дифференцированию, и таблицы производных.
Справедливость каждой формулы можно проверить путем дифференцирования правой части.
 |  | ||
 , n ≠ ‒1 , n ≠ ‒1 |  | ||
 | 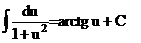 | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  |
Интегралы, содержащиеся в данной таблице, называются табличными.
Замечание
Переменную u, входящую в формулы таблицы, можно заменить любой другой переменной или выражением.
Пример 2.


Интегрирование по частям
Таблица интегралов не содержит формул для вычисления интеграла от произведения двух функций, от логарифмической и обратных тригонометрических функций. Эти интегралы находятся методом интегрирования по частям.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
Данный метод базируется на следующей теореме.
Т.4.2. (интегрирование по частям в неопределенном интеграле)
Пусть функции u = u(x) и v = v(x) определены и дифференцируемы на некотором промежутке Х. Если на этом промежутке существует интеграл òv(x)u′(x)dx, то на нем существует и интеграл
òu(x)v′(x)dx, причем справедливо равенство
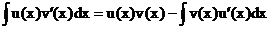 (2)
(2)
Формула (2) называется формулой интегрирования по частям в неопределенном интеграле.
Так как v′(x)dx = dv и u′(x)dx = du, то формулу (2) можно записать в виде
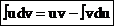 . (3)
. (3)
Формула (3) – формула интегрирования по частям –позволяет свести вычисление интеграла òudv к вычислению интеграла òvdu, который может оказаться существенно более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям (3). Иногда эту формулу приходиться использовать несколько раз.
ТЕМА 6. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1.Первообразная функция.
2.Понятие неопределенного интеграла и его свойства.
3.Таблица основных интегралов.
4.Методы интегрирования.
Одной из основных задач дифференциального исчисления является отыскание производной или дифференциала заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике, химии и технике приводят к обратной задаче: по заданной функции f(x) найти такую функцию F(x), производная которой была бы равна функции f(x), т.е. F′(x) = f(x).
Операция восстановления функции по известной производной этой функции называется интегрированием, а раздел математики, изучающий способы нахождения функции по ее производной и приложения этой операции, называется интегральным исчислением.
