Фотон с энергией 0,25 МэВ рассеялся на свободном электроне. Энергия рассеянного фотона 0,2 МэВ. Определить угол рассеяния.
Энергия рассеянного фотона 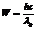 , энергия падающего фотона
, энергия падающего фотона 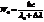 , =>
, => 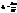 ,
, 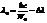 ,
,
отсюда находим изменение 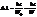 , используя выражение
, используя выражение 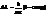 , получаем
, получаем 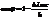
Фотон с энергией 1,2 МэВ был рассеян в результате эффекта Комптона на угол 90°. Найти энергию и длину волны рассеянного фотона.
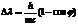 , энергия падающего фотона
, энергия падающего фотона 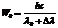 ,
, 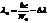 , тогда энергия рассеян. фотона
, тогда энергия рассеян. фотона 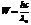 ,
, 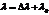
Х
Характеристическая температура Дебая Температура Дебая — температура, при которой возбуждаются все моды колебаний в данном твёрдом теле. Дальнейшее увеличение температуры не приводит к появлению новых мод колебаний, а лишь ведёт к увеличению амплитуд уже существующих, т. е. средняя энергия колебаний с ростом температуры растёт. Температура Дебая — физическая константа вещества, характеризующая многие свойства твёрдых тел — теплоёмкость, электропроводность, теплопроводность, уширение линий рентгеновских спектров, упругие свойства и т. п. Введена впервые П. Дебаем в его теории теплоёмкости. 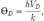
Температура Дебая определяется следующей формулой:
где h — постоянная Планка, VD — максимальная частота колебаний атомов твёрдого тела, k — постоянная Больцмана.Температура Дебая приближённо указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.
Ч
Человек с лодки рассматривает предмет, лежащий на дне водоема (n = 1,33). Определите его глубину, если при определении «на глаз» по вертикальному направлению глубина водоема кажется равной 1,5 м.
Преломленный луч падающий, луч преломленный и перепенд, провед к границе раздела в точке падения, лежат в одной плоскости отношение sin угла падения к sin угла преломления есть величина постоянная для данных сред. Sini1/sini2=n21, где n21-отн показ преломления 2-ой среды отн 1-ой. За счет преломления света к поверх воды каждая глубина меньше реальной. По данному рис запишем:htga1=Нtga2. Отсюда выражаем Н=h tga1/tga2. при малых углах отнош тангенса заменяется отношением синусов. Тогда tg a1/tga2=sina1/sina2=n21 следов получаем H=hn=1.5*1.33=2 м
Чем обусловлено двойное лучепреломление в анизотропных кристаллах?
Происходящее вследствие зависимости показателя преломления среды от направления напряженности электрического поля световой волны. Световая волна в анизотропных веществах распадается на 2 волны – обыкновенную и необыкновенную с взаимно перпендикулярными плоскостями поляризации света.
Чем объясняется разнообразие окраски крыльев бабочек, хотя красящий пигмент в них отсутствует?
Исходя из условия максимума: 2d(√n2 - sin2α) + λ/2 = λ/2π * 2mπ или
2d(√n2 - sin2α) = (2m-1) λ/2
Исходя из условий минимума: 2d(√n2 - sin2α) + λ/2 = λ/2π * (2m+1) или
2d(√n2 - sin2α) = mλ
Условия интерференционных максимумов и минимумов для разных длин волн в отраженном свете будет выполняться на участках пленки с различной толщиной. Именно этим, а вовсе не наличием красящего пигмента, и объясняется радужная окраска крыльев бабочек.
