Дифракция Френеля от круглого отверстия.

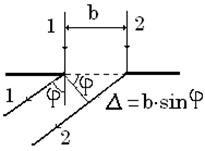Пусть на пути световой волны находится непрозрачный экран с круглым отверстием радиуса r₀. Для данного случая справедливо соотношение:

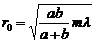. (3)

Определим из (3) число открытых зон Френеля: 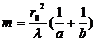. (4)

Запишем выражение для амплитуды в т. Р:

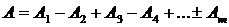. (5)

или

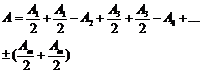. (5^/)

Далее

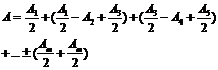
Если m – нечетное, то

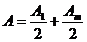. (6) (максимум I)

Если m – четное, то

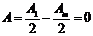. (7) (минимум I)

Дифракция от круглого диска. Здесь всегда в центре максимум.

Первые m зон закрыты, следовательно:

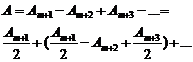
или

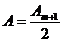. (8)

Все формулы справедливы при малых m.

Рис. 2

Дифракция Фраунгофера на щели

Если на оптической разности хода укладывается четное число зон Френеля, получим минимум:

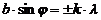, (9)

откуда 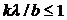и 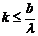. (10)

Интенсивность 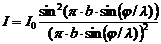. (11)

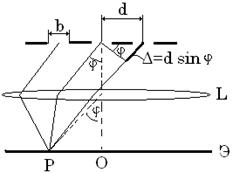
Дифракционная решетка

Это – совокупность одинаковых щелей, отстоящих на одинаковом расстоянии друг от друга. Период(постоянная) решетки – расстояние между серединами соседних щелей.

Схема на рис.3:

Интенсивность:

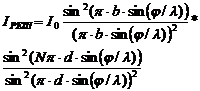
Условие min для щели и решетки одинаковы:

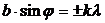, k = 1,2,3…

Условие главных мах:

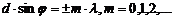(12)

Рис. 3

Условие дополнительных min:

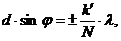(13)

где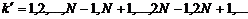

Их число равно (N-1) в промежутках между соседними главными максимумами. 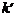принимает все целочисленные значения, кроме 0, N, 2N…

Число главных мах равно

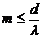. (14)

Интенсивность главных мах растет пропорционально квадрату числа щелей:

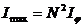. (15)

Положение главных максимумов зависит от λ. Красные лучи, в отличие от дисперсионного спектра, отклоняются сильнее, чем фиолетовые. Дифракционная решетка работает как спектральный прибор, разлагая белый свет в спектр.

Угловая дисперсия

.

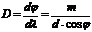Линейная дисперсия

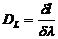
Разрешающая способность

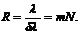
26 Монохроматическая волна вида 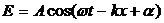представляет собой бесконечную во времени и пространстве последовательность «горбов» и «впадин», перемещающихся по оси Х с фазовой скоростью 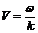. Но такая волна не может нести полезной информации. Для этого ее надо оборвать и поместить на ней полезный сигнал. Тогда это уже не будет монохроматической волной.

Проще всего передать сигнал с помощью светового импульса (см. анимацию). Такой импульс по теореме Фурье можно представить в виде суперпозиции волн вышеуказанного типа с частотами, заключенными в некотором интервале 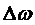. Группой волн иливолновым пакетом называется суперпозиция волн, мало отличающихся по частоте.

Ее можно выразить в виде

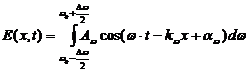. (18)

Для группы волн справедливы соотношения:

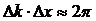и . (19)

В отсутствие дисперсии (нет зависимости скорости волн от длины волны или частоты) все плоские волны распространяются с одинаковой фазовой скоростью V. Скорость движения группы волн совпадает с V и форма пакета сохраняется. В диспергирующей среде пакет расплывается. При небольшой дисперсии группе волн можно приписать скорость u перемещения центра пакета или группы волн. Ее называют групповой скоростью.

Напомним 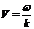- фазовая скорость. Групповая скорость определяется как

.

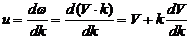Последний сомножитель выразим в виде

.

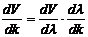С учетом 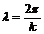получим .

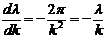Тогда

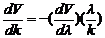
и

.

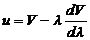Видно, что в зависимости от знака 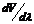групповая скорость может быть больше или меньше фазовой скорости V. Групповая скорость равна скорости переноса энергии волной.