Способы наблюдения интерференции

Принцип наблюдения интерференции от естественных источников мы уже рассмотрели. Используются зеркала Френеля (рис.3), бипризма Френеля (рис.5). Расчеты для них во многих учебниках имеются.

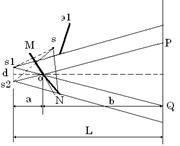
Рис.3

Рассмотрим подробнее интерференцию в тонких пленках.

На рис.4 разность хода лучей 1 и 2 в точке С равна:

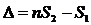. (12)

Видно, что S₁ = ВС; S₂ = AO + OC;

КС = b* tgβ ; Тогда

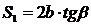и .

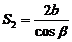Рис. 4

Подставим их в (12):

.

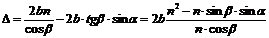Сделаем замену

.

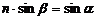Получим

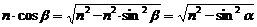.Подставив последнее выражение в Δ, получим

.

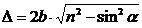При отражении луча 1 в точке С от оптически более плотной среды фаза изменяется на π. Окончательное выражение для разности хода:

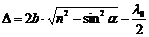. (13)

Условия когерентности: Δ ‹ ℓ _КОГ, т.е.

,

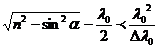или

.

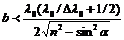Тогда

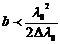. (14)

Таким образом, отраженные волны будут когерентными только при выполнении условия (14), т.е. когда удвоенная толщина пластины меньше длины когерентности.

Пример: 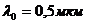, 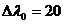А. Тогда 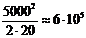А = 0,06 (мм)

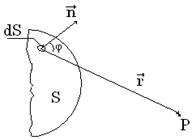
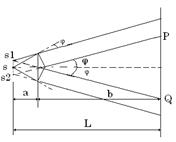
Рис. 5 Бипризма Френеля

24 Под дифракциейпонимают явления, наблюдаемые при распространении света в среде с резкими неоднородностями. В частности, наблюдается огиба­ние световыми волнами препятствий и проникновение света в область геометрической тени.

Условие дифракции: d ~ λ.

Дифракция, как и интерференция, проявляется в перераспределении светового потока при наложении когерентных волн. Различие: при интерференции рассматривается конечное число источников света, при дифракции – непрерывно расположенные.

Схема наблюдения дифракции: источник - непрозрачная преграда - экран.

Два вида дифракции: Френеля для сферических волн, Фраунгофера – для плоских.

Принцип Гюйгенса-Френеля

Принцип Гюйгенса объясняет проникновение света в область тени, но не дает сведений об амплитуде волн. Согласно принципу Г-Ф учет амплитуд и фаз вторичных волн при их интерференции позволяет найти амплитуду результирующей волны в любой точке.

От каждого участка dS волновой поверхности S в точку Р приходит колебание

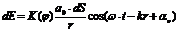(1)

и для всей поверхности S

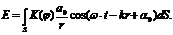(2)

К(φ) = 1 при φ = 0; К(φ) = 0 при φ = π/2.

Рис. 1

Расчет по (2) –очень сложная задача, но при определенной симметрии по методу зон Френеля определение амплитуды сильно упрощается.

Суть метода: От точечного источника S распространяется сферическая волна. Волновые поверхности симметричны относительно SP. Волновую поверхность разобъем на равные по площади кольцевые зоны так, чтобы расстояния от краев каждой зоны до т. Р отличались на λ/2. Тогда колебания в т. Р от 2-х соседних зон приходят в противофазе и, поскольку амплитуды от равных площадей волновой поверхности считаются одинаковыми (по Френелю), то при четном числе зон в т. Р будет максимум интенсивности (амплитуды), а при нечетном – максимум.

Метод зон Френеля позволил на основе волновой теории объяснить закон прямолинейного распространения света. Рассмотрим 2 примера: