Закон Стефана–Больцмана. Закон Вина.

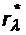На рисунке 1 представлены экспериментальные кривые зависимости излучательной способности (спектральной плотности энергетической светимости) АЧТ от длины волны при постоянных температурах.

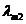
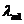
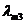
Рис.1 Зависимость излучательной способности АЧТ от длины волны при 1600К,

1700К и 1800К.

Как видно из рисунка излучательная способность АЧТ возрастает с повышением температуры, а ее максимум с увеличением температуры смещается в область более коротких волн. Площадь под кривой равна энергетической светимости АЧТ .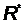

Закон Стефана–Больцмана: энергетическая светимость АЧТ 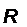пропорциональна четвертой степени его температуры

,

где s = 5,67×10^-8Вт×м^-2К^-4 - постоянная Стефана-Больцмана. Для серого тела 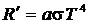, где – поглощательная способность серого тела.

Закон смещения Вина:выражает зависимость положения максимума функции от температуры:

где 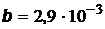м×К – постоянная Вина, 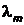– длина волны, на которую приходится максимум излучательной способности АЧТ. Этот закон выполняется и для серых тел.

Формула Рэлея–Джинсадля излучательной способности АЧТ.

Рэлей и Джинс попытались получить вид функции в рамках классической статистической физики, в соответствии с которой тело испускает и поглощает энергию непрерывно. Вычисления привели к формуле:

,

где 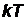– средняя энергия осциллятора с собственной частотой n, 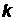– постоянная Больцмана, 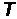– абсолютная температура, с – скорость света в вакууме.

Полученная зависимость хорошо согласуется с экспериментом при малых частотах (больших длинах волн), т.е. при условии hn << kT, но дает неверный результат при больших частотах. Функция не имеет максимума, монотонно возрастает, а интеграл от этой функции, т.е. полная энергия излучения, равен бесконечности. Эта ситуация была названа современниками ультрафиолетовой катастрофой.

Формула Планка.

Функцию излучательной способности АЧТ, согласующуюся с опытными данными, удалось получить М. Планку в 1900 году. Для этого ему пришлось предположить, что электромагнитная энергия излучается АЧТ порциями (квантами), энергия которых пропорциональна частоте излучения , где 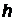=6,63×10^-34Дж×с –коэффициент пропорциональности, получивший название постоянной Планка, n–частота излучения.

Формула Планка имеет вид:

, , ,

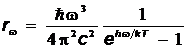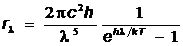где – испускательные способности АЧТ, 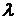– длина волны, n – частота, w – циклическая частота, с – скорость света в вакууме, 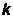– постоянная Больцмана, – абсолютная температура, 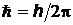– приведенная постоянная Планка ( 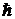= 1,05×10^–34 Дж×с).

Средняя мощность излучения в интервале длин волн Dl: , здесь – излучательная способность АЧТ, S – площадь излучающей поверхности.

При формула Планка переходит в формулу Рэлея-Джинса

,

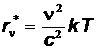а при – в формулу Вина, которая ранее была получена эмпирически

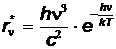
Примеры решения задач

Задача 1.Исследование спектра излучения Солнца показывает, что максимум его излучательной способности соответствует длине волны, равной 500 нм. Принимая Солнце за АЧТ, определите:

1. энергетическую светимость Солнца;

2. поток энергии, излучаемой Солнцем.

Решение. 1. Выразим температуру излучающей поверхности из закона смещения Вина

и, подставив в закон Стефана-Больцмана, для энергетической светимости, получим:

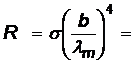6,4·10⁷ Вт/м².

2. Поток энергии, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности: 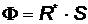, ( , где 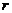- радиус Солнца, равный 6,98×10⁸ м). Таким образом, . Произведя вычисления, получим Вт.

Задача 2.Внутренняя поверхность муфельной печи при открытом отверстии диаметром = 5 см имеет температуру Т равную 1000 К. Считая, что отверстие излучает как АЧТ, определите, какая доля мощности рассеивается внешними стенками печи, если мощность P, потребляемая печью, составляет 500 Вт.

Решение. После установления режима теплового равновесного печи доля мощности, рассеиваемой внутренней поверхностью печи:

,

где - мощность излучения, испускаемого отверстием , - энергетическая светимость, - площадь отверстия печи. Окончательно получим:

= 96,1%

Задача 3.АЧТ находится при температуре 1500 К. При остывании тела длина волны, соответствующая максимуму излучательной способности, изменилась на 5 мкм. Определите температуру, до которой охладилось тело.

Решение.В соответствии с законом Вина при остывании тела длина волны, приходящаяся на максимум излучения, смещается в сторону более длинных волн. Тогда и для температуры тела после остывания получим:

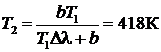
Задача 4.Диаметр спирали в электрической лампочке d = 0,3 мм, длина спирали 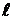= 5 см. При включении лампочки в сеть напряжением U = 127 В черезлампочку течет ток I = 0,31 А. Найдите температуру спирали. Считать, что приус-

тановившемся равновесии все выделяющееся в нити тепло теряется в результате излучения. Отношение энергетической светимости вольфрама и АЧТ а = 0,31.

Решение. По условию задачи электрическая мощность, потребляемая спиралью, равна мощности теплового излучения

,

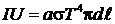тогда

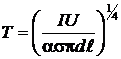= 2600 К.

Внешний фотоэффект

Внешний фотоэлектрический эффект -испускание электронов из вещества под действием света (излучения). Если электроны вылетают за пределы вещества, то фотоэффект называют внешним. Он наблюдается главным образом у металлов. Вылетающие с поверхности металла электроны называют фотоэлектронами, а регистрируемый в цепи ток – фототоком.

Фотоэффект был открыт Герцем в 1887 г. Столетов изучал фотоэффект на установке, изображенной на Рис.2а, которая позднее была усовершенствована другими исследователями (Рис.2б)

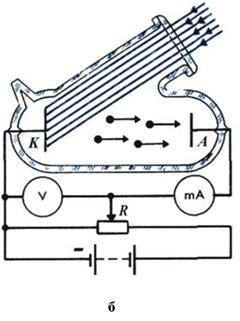
Рис.2а – схема установки Столетова, где А – источник излучения, B - источник Э.Д.С., С – конденсатор, состоящий из проволочной сетки и сплошной пластины, G – гальванометр; б – установка Ленарда и других исследователей для изучения фотоэффекта, где К и А – катод и анод фотоэлемента, V – вольтметр, mA - миллиамперметр, измеряющий фототок, R - реостат.

Герцем и Столетовым были установлены следующие законы фотоэффекта:

1. Максимальная сила фототока (тока насыщения) пропорциональна световому потоку, падающему на катод.

2. Максимальная скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока.

3. Независимо от интенсивности светового потока фотоэффект начинается только при определенной для данного металла минимальной частоте (максимальной длине волны) света, называемой красной границей фотоэффекта.

Классическая теория не смогла объяснить законы фотоэффекта. Чтобы сделать это А. Эйнштейн предположил, что свободный электрон проводимости в металле поглощает квант света . Часть энергии поглощенного (и переставшего существовать) кванта, полученная электроном, затрачивается на работу выхода 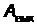из металла, которую он совершает против сил притяжения со стороны положительного заряда ионов кристаллической решетки. Кроме того, между электронами проводимости в металле и электронами, вылетевшими из металла в результате термоэлектронной эмиссии устанавливается динамическое равновесие и возникает тонкий запирающий слой, напряженность электрического поля которого направлена наружу (по отношению к поверхности металла). Электрон, вылетающий из металла в результате фотоэффекта должен преодолеть этот запирающий слой.

Закон сохранения энергии для фотоэффекта (формула Эйнштейна) имеет вид:

,

где 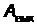– работа выхода электрона из вещества, 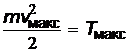–максимальная кинетическая энергия электрона, 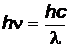– энергия поглощенного кванта, –постоянная Планка, – масса электрона.

Если электрон поглощает квант света не у самой поверхности, а на некоторой глубине, то часть его кинетической энергии может быть потеряна в результате случайных столкновений в металле. Кинетическая энергия электрона будет максимальной, если электрон избежит указанных столкновений.

Из уравнения Эйнштейна следует, что , зависит от частоты излучения, но не зависит от его интенсивности.

Вольтамперная характеристика(зависимость фототока 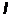от анодного на пряжения )

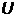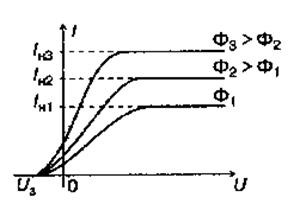
Рис. 3. Вольтамперные характеристики фотоэлемента для одной частоты падающего излучения и разных световых потоков .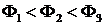

Характер кривых вольтамперных характеристик фотоэлемента (Рис.3) объяс-няется следующим образом. Электроны вылетают из катода с различными по величине скоростями. При U = 0 лишь часть испущенных электронов, обладающих достаточно большими скоростями, достигает анода. При некотором положительном напряжении (U > 0) фототок достигает насыщения - все электроны, испущенные катодом, попадают на анод. Чем больше световой поток Ф, тем больше квантов света поглощается электронами в единицу времени, тем больше электронов вылетает из металла и, следовательно, тем больше ток насыщения I_н = k·Ф. Для прекращения фототока необходимо приложить достаточное по величине отрицательное напряжение U_з, называемое задерживающим. В этом случае выполняется условие (e — заряд электрона, m — его масса, — задерживающее напряжение) и ни одному из электронов не удастся преодолеть задерживающее электрическое поле и достичь анода. Вольтамперная характеристика позволяет определить число электронов, вылетающих из катода в единицу времени и максимальную кинетическую энергию электронов, которая выражается через задерживающее напряжение. Коэффициент пропорциональности k (мкА/Вт), соответствующий силе фототока (выраженной в микроамперах) при освещенности катода световым потоком 1 Вт, называют фоточувствительностью элемента. Фототок насыщения I_н = е·n, где n — число электронов, испускаемых катодом в 1 с. Зависимость фототока насыщения от светового потока носит название световой характеристики фотоэлемента (Рис. 4).

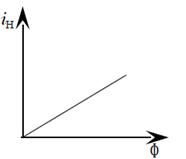
Рис.4 Световая характеристика фотоэлемента

Поскольку 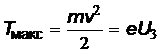, то уравнение Эйнштейна можно записать в виде:

.

В случае если энергия фотона много больше работы выхода ( ), то

Внешний фотоэффект считается состоявшимся, если электрон выходит из металла с нулевой скоростью. Максимальная длина волны 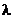падающего кванта или минимальная частота n₀, w₀, при которой это происходит, называется красной границей фотоэффекта.

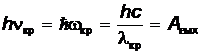
Красной граница фотоэффекта называется потому, что увеличение длины волны падающего света до максимально возможной соответствует смещению в сторону красной границы для видимого спектра. При меньшей частоте падающего света (большей длине волны) фотоэффект не наблюдается.

Энергию фотонов и работу выхода принято выражать во внесистемных единицах - электронвольтах (эВ). Один электронвольт равен энергии, приобретенной электроном при прохождении разности потенциалов 1В: 1 эВ = 1,6×10^-19 Дж.

Экспериментально было обнаружено, что зависимость 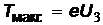от n для данного металла имеет вид наклонной прямой, причем наклон прямых, построенных для разных металлов, оказался одинаковым.

Из соотношения вытекает уравнение, соответствующее экспериментальной зависимости, показанной на Рис.5,

.

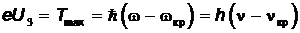Рис. 5 Зависимость максимальной кинетической энергии фотоэлектронов от частоты падающего света

Если электрон в металле является свободным (не связанным с атомом), то фотоэффект не состоится. Законы сохранения импульса и энергии для фотоэффекта в этом случае имели бы вид (до взаимодействия с фотоном электрон покоился):

,

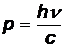
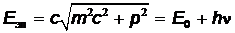где p – импульс электрона, - энергия покоя электрона; - энергия электрона, который после поглощения фотона приобрел импульс .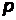

Возведя полученные соотношения в квадрат, получим

.

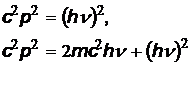При эти равенства несовместимы, откуда следует, что свободный электрон не может поглотить фотон.

Задача 1. Определите максимальную скорость фотоэлектронов, вырываемых с поверхности серебра:

1. ультрафиолетовым излучением с длиной волны 155 нм;

2. g - излучением с длиной волны 2,47 пм.

Работа выхода электрона из серебра равна 4,7 эВ.

Решение.Кинетическаяэнергия фотоэлектрона зависит от энергии фотона

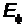, вызывающего фотоэффект. Если энергия фотона много меньше энергии покоя

электрона , то кинетическая энергия фотоэлектрона выражается по классической формуле , а если сравнима по величине или больше , то по релятивистской .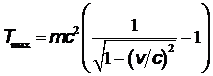

1. Энергия фотона 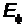равна:

Дж = 8 эВ,

что много меньше энергии покоя электрона 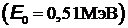. Поэтому максимальная кинетическая энергия фотоэлектрона выражается по классической формуле из уравнения Эйнштейна 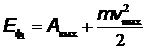, и равна

=1,08×10⁶м/с.

2. Энергия фотона g - излучения 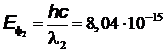Дж = 0,502 МэВ

сравнима с энергией покоя электрона, поэтому для вычисления его кинетической энергии необходимо использовать релятивистскую формулу. Работа выхода ( = 4,7 эВ) много меньше энергии g - фотона, поэтому ею можно пренебречь:

Выполнив преобразования, из уравнения Эйнштейна найдем

=0,755,

м/с.

Задача 2. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найдите длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.

Решение.Найдем длину волны из уравнения Эйнштейна .

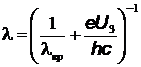= 196 нм.

Задача 3. Какую часть энергии фотона составляет энергия, которая пошла на совершение работы выхода электронов из металла, если длина волны для красной границы равна 0,54 мкм, а максимальная кинетическая энергия фотоэлектронов 0,5эВ?

Решение.Из формулы Эйнштейна для фотоэффекта 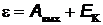получим 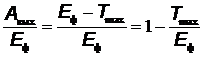, где 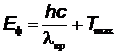= 4,48×10^-19 Дж = 2,8 эВ.

Тогда , то есть составляет 82%.

Задача 4. Возникает ли фотоэффект в цинке под действием излучения, имеющего длину волны 0,45 мкм? Работа выхода электронов из цинка равна 4,2 эВ.

Решение.Минимальная энергия кванта, вызывающего фотоэффект, равна работе выхода. Энергия кванта по условию задачи равна 2,75 эВ, что меньше работы выхода. Поэтому фотоэффекта не будет.

Задача 5. Металлический шар радиусом 10 см облучают светом с длиной волны 200 нм. Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна 7,2×10^–19 Дж.

Решение. На шаре установится такой заряд, что под действием его электростатического поля самые быстрые электроны, покидающие поверхность шара вследствие фотоэффекта, вернутся на положительно заряженный шар. В этом случае вы

полняется равенство 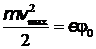, где 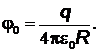Из уравнения Эйнштейна получим 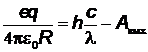, откуда

= 1,9×10^–11 Кл.

Задача 6. Фотоны с длиной волны 330 нм вырывают электроны из металла с работой выхода 2,9 эВ. Найдите максимальный импульс, передаваемый поверхности металла при вылете каждого электрона в результате фотоэффекта. Считать, что электрон вылетает нормально к поверхности катода навстречу падающему фотону.

Решение.Закон сохранения импульса для фотоэффекта имеет вид (рис.6):

_,

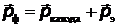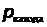
фотокатод

Рис.6

где – импульс фотона, 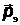– максимальный импульс электрона, 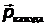– импульс, полученный поверхностью катода. Из уравнения Эйнштейна импульс падающего фотона

.

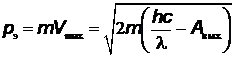Импульс, передаваемый поверхности, равен сумме импульса фотона и импульса вылетевшего фотоэлектрона.

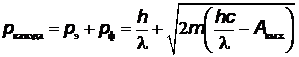= 5×10^–25 кг×м/с.