С.Г.Серебряков, Д.Д.Ходкевич

С.Г.Серебряков, Д.Д.Ходкевич

ОСНОВЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ И ЭЛЕМЕНТЫ ФИЗИКИ ТВЕРДОГО ТЕЛА

Учебное пособие для студентов 2 курса

Под редакцией проф. А.И.Черноуцана

Москва 2011

Рассмотрены все вопросы, входящие в программу физики (базовый уровень) ФГОС ВПО третьего поколения по разделам «квантовая физика» и «ядерная физика». Приведены примеры решения 42 задач.

Для самостоятельной работы студентов всех специальностей и подготовки к экзамену.

Содержание

	Предисловие
I. Основы квантовой физики
1.	Законы теплового излучения
2.	Внешний фотоэффект
3.	Дуализм свойств электромагнитного излучения.
4.	Эффект Комптона
5.	Теория Бора для атома водорода и водородоподобного иона
II. Элементы квантовой механики
6.	Волны де Бройля
7.	Соотношения неопределенностей Гейзенберга
8.	Волновая функция. Уравнение Шредингера
9.	Решение уравнения Шредингера для движения частицы в одномерной бесконечной потенциальной яме.
10.	Уравнение Шредингера для гармонического осциллятора
III. Основы атомной физики
11.	Уравнение Шредингера для атома водорода
12.	Квантование момента импульса. Квантовые числа
13.	Спин и магнитный момент электрона
14.	Принцип Паули
15.	Вынужденное излучение. Лазеры
IУ. Элементы физики твердого тела
16.	Статистика Бозе-Эйнштейна и Ферми-Дирака
17.	Свободные электроны в металле
18.	Сверхпроводимость и сверхтекучесть
19.	Образование энергетических зон в кристалле
20.	Собственные и примесные полупроводники
21.	p-n- переход
У. Элементы ядерной физики
22.	Свойства атомных ядер
23.	Ядерные силы
24.	Закон радиоактивного распада
25.	Альфа-распад
26.	Бета - распад
27.	Гамма - излучение и его взаимодействие с веществом
28.	Реакция деления тяжелых ядер.
29.	Проблемы управляемого термоядерного синтеза легких ядер
30.	Элементарные частицы
31.	Литература

Предисловие

Предлагаемое учебное пособие базируется на курсе лекций, читавшихся авторами более двадцати лет на факультетах разработки и эсплуатации месторождений нефти и газа, инженерной механики, геологии, геофизики и геохимии, химико-технологическом и автоматики и вычислительной техники. Материал лекций был тщательно переработан для того, чтобы соответствовать базовому уровню программы по физике для бакалавров, вводимой с 1 сентября 2011 года федеральным государственным стандартом высшего специального образования третьего поколения. В пособие были включены разделы, посвященные современному состоянию теории элементарных частиц и проблемы создания управляемого термоядерного реактора. Все разделы пособия были дополнены необходимыми иллюстрациями и примерами решения основных типовых задач.

Пособие рассчитано на студентов РГУ нефти и газа. В пособии кратко изложены все вопросы разделов программы: «квантовая физика» и «ядерная физика» и приведены примеры решения основных задач. Самостоятельная работа студентов с пособием позволяет подготовиться контрольной, зачету и экзамену по соответствующему разделу программы по физике практически без привлечения других учебников и учебных пособий.

Авторы выражают благодарность проф. Л.К. Белоухову и доц. И.Н. Жетвиной за внимательное прочтение рукописи и ряд ценных замечаний.

I. ОСНОВЫ КВАНТОВОЙ ФИЗИКИ

Законы теплового излучения

Тепловое излучение–излучение телом электромагнитных волн за счет его внутренней энергии. Тепловое излучение происходит при переходе атома с одного энергетического уровня на другой в результате теплового движения. Тепловое излучение наблюдается при любой температуре и характеризуется сплошным спектром (непрерывный ряд длин волн) с максимумом интенсивности при определенной длине волны, зависящей от температуры.

При термодинамическом равновесии само тепловое излучение является равновесным. Если нагретые (излучающие) тела поместить в полость, ограниченную идеально отражающей оболочкой, то через некоторое время в результате непрерывного обмена энергией между телами и излучением, заполняющим полость, температура всех тел станет одинаковой и наступит равновесие, т.е. каждое тело в единицу времени будет поглощать в среднем столько же энергии, сколько и излучать. В соответствии с законами термодинамики в полости устанавливается хаотическое состояние излучения, которому соответствует наибольшая вероятность. Оно и называется равновесным. Плотность равновесного излучения, его распределение по спектру частот и направлениям распространения не зависят от формы и материалов стенок полости и определяются только температурой стенок полости. Поскольку излучение находится в тепловом равновесии со стенками, то можно говорить не только об их температуре, но и о температуре самого излучения. Температура равновесного излучения есть свойство самого излучения, а не стенки, с которой оно находится в тепловом равновесии. О температуре равновесного излучения можно говорить и в отсутствии полости.

Закон Кирхгофа.

Если система состоит из нескольких тел, нагретых до различной температуры, то спустя некоторое время произойдет выравнивание температур: горячие тела, излучая, передадут холодным энергии больше, чем получат от них, а холодные тела поглотят больше энергии, чем отдадут при излучении. Этот процесс будет происходить до тех пор, пока не наступит термодинамическое равновесие. При неизменной температуре, а, следовательно, и энергии тел тело с большей излучательной способностью r_w будет больше излучать. Для компенсации потерянной при этом энергии оно должно будет больше поглощать, т.е. обладать большей поглощательной способностью a_w. Отношение излучательной способности любого тела к его поглощательной способности будет выражаться универсальной функцией длины волны и температуры:

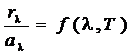
Поскольку поглощательная способность АЧТ равна единице, то эта функция является излучательной способностью АЧТ :

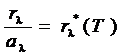
Закон Кирхгофа: отношение излучательной способности тела к его поглощательной способности при данной температуре одинаково для всех тел и равно излучательной способности АЧТ.

При одной и той же температуре АЧТ обладает наибольшей излучательной способностью и энергетической светимостью. Для серых тел энергетическая светимость .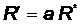

Формула Планка.

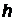Функцию излучательной способности АЧТ, согласующуюся с опытными данными, удалось получить М. Планку в 1900 году. Для этого ему пришлось предположить, что электромагнитная энергия излучается АЧТ порциями (квантами), энергия которых пропорциональна частоте излучения , где =6,63×10^-34Дж×с –коэффициент пропорциональности, получивший название постоянной Планка, n–частота излучения.

Формула Планка имеет вид:

, , ,

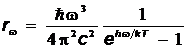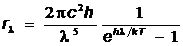где – испускательные способности АЧТ, 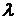– длина волны, n – частота, w – циклическая частота, с – скорость света в вакууме, 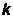– постоянная Больцмана, – абсолютная температура, 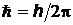– приведенная постоянная Планка ( 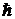= 1,05×10^–34 Дж×с).

Средняя мощность излучения в интервале длин волн Dl: , здесь – излучательная способность АЧТ, S – площадь излучающей поверхности.

При формула Планка переходит в формулу Рэлея-Джинса

,

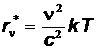а при – в формулу Вина, которая ранее была получена эмпирически

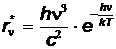
Примеры решения задач

Задача 1.Исследование спектра излучения Солнца показывает, что максимум его излучательной способности соответствует длине волны, равной 500 нм. Принимая Солнце за АЧТ, определите:

1. энергетическую светимость Солнца;

2. поток энергии, излучаемой Солнцем.

Решение. 1. Выразим температуру излучающей поверхности из закона смещения Вина

и, подставив в закон Стефана-Больцмана, для энергетической светимости, получим:

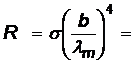6,4·10⁷ Вт/м².

2. Поток энергии, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности: 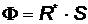, ( , где 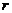- радиус Солнца, равный 6,98×10⁸ м). Таким образом, . Произведя вычисления, получим Вт.

Задача 2.Внутренняя поверхность муфельной печи при открытом отверстии диаметром = 5 см имеет температуру Т равную 1000 К. Считая, что отверстие излучает как АЧТ, определите, какая доля мощности рассеивается внешними стенками печи, если мощность P, потребляемая печью, составляет 500 Вт.

Решение. После установления режима теплового равновесного печи доля мощности, рассеиваемой внутренней поверхностью печи:

,

где - мощность излучения, испускаемого отверстием , - энергетическая светимость, - площадь отверстия печи. Окончательно получим:

= 96,1%

Задача 3.АЧТ находится при температуре 1500 К. При остывании тела длина волны, соответствующая максимуму излучательной способности, изменилась на 5 мкм. Определите температуру, до которой охладилось тело.

Решение.В соответствии с законом Вина при остывании тела длина волны, приходящаяся на максимум излучения, смещается в сторону более длинных волн. Тогда и для температуры тела после остывания получим:

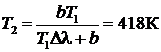
Задача 4.Диаметр спирали в электрической лампочке d = 0,3 мм, длина спирали 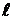= 5 см. При включении лампочки в сеть напряжением U = 127 В черезлампочку течет ток I = 0,31 А. Найдите температуру спирали. Считать, что приус-

тановившемся равновесии все выделяющееся в нити тепло теряется в результате излучения. Отношение энергетической светимости вольфрама и АЧТ а = 0,31.

Решение. По условию задачи электрическая мощность, потребляемая спиралью, равна мощности теплового излучения

,

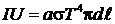тогда

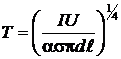= 2600 К.

Внешний фотоэффект

Внешний фотоэлектрический эффект -испускание электронов из вещества под действием света (излучения). Если электроны вылетают за пределы вещества, то фотоэффект называют внешним. Он наблюдается главным образом у металлов. Вылетающие с поверхности металла электроны называют фотоэлектронами, а регистрируемый в цепи ток – фототоком.

Фотоэффект был открыт Герцем в 1887 г. Столетов изучал фотоэффект на установке, изображенной на Рис.2а, которая позднее была усовершенствована другими исследователями (Рис.2б)

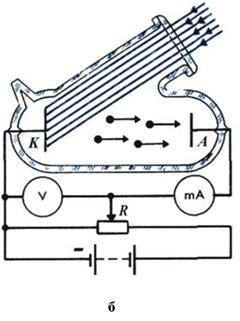
Рис.2а – схема установки Столетова, где А – источник излучения, B - источник Э.Д.С., С – конденсатор, состоящий из проволочной сетки и сплошной пластины, G – гальванометр; б – установка Ленарда и других исследователей для изучения фотоэффекта, где К и А – катод и анод фотоэлемента, V – вольтметр, mA - миллиамперметр, измеряющий фототок, R - реостат.

Герцем и Столетовым были установлены следующие законы фотоэффекта:

1. Максимальная сила фототока (тока насыщения) пропорциональна световому потоку, падающему на катод.

2. Максимальная скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока.

3. Независимо от интенсивности светового потока фотоэффект начинается только при определенной для данного металла минимальной частоте (максимальной длине волны) света, называемой красной границей фотоэффекта.

Классическая теория не смогла объяснить законы фотоэффекта. Чтобы сделать это А. Эйнштейн предположил, что свободный электрон проводимости в металле поглощает квант света . Часть энергии поглощенного (и переставшего существовать) кванта, полученная электроном, затрачивается на работу выхода 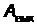из металла, которую он совершает против сил притяжения со стороны положительного заряда ионов кристаллической решетки. Кроме того, между электронами проводимости в металле и электронами, вылетевшими из металла в результате термоэлектронной эмиссии устанавливается динамическое равновесие и возникает тонкий запирающий слой, напряженность электрического поля которого направлена наружу (по отношению к поверхности металла). Электрон, вылетающий из металла в результате фотоэффекта должен преодолеть этот запирающий слой.

Закон сохранения энергии для фотоэффекта (формула Эйнштейна) имеет вид:

,

где 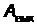– работа выхода электрона из вещества, 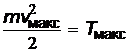–максимальная кинетическая энергия электрона, 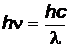– энергия поглощенного кванта, 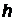–постоянная Планка, 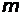– масса электрона.

Если электрон поглощает квант света не у самой поверхности, а на некоторой глубине, то часть его кинетической энергии может быть потеряна в результате случайных столкновений в металле. Кинетическая энергия электрона будет максимальной, если электрон избежит указанных столкновений.

Из уравнения Эйнштейна следует, что , зависит от частоты излучения, но не зависит от его интенсивности.

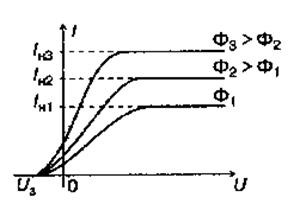Вольтамперная характеристика(зависимость фототока 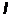от анодного на пряжения )

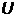Рис. 3. Вольтамперные характеристики фотоэлемента для одной частоты падающего излучения и разных световых потоков .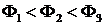

Характер кривых вольтамперных характеристик фотоэлемента (Рис.3) объяс-няется следующим образом. Электроны вылетают из катода с различными по величине скоростями. При U = 0 лишь часть испущенных электронов, обладающих достаточно большими скоростями, достигает анода. При некотором положительном напряжении (U > 0) фототок достигает насыщения - все электроны, испущенные катодом, попадают на анод. Чем больше световой поток Ф, тем больше квантов света поглощается электронами в единицу времени, тем больше электронов вылетает из металла и, следовательно, тем больше ток насыщения I_н = k·Ф. Для прекращения фототока необходимо приложить достаточное по величине отрицательное напряжение U_з, называемое задерживающим. В этом случае выполняется условие (e — заряд электрона, m — его масса, — задерживающее напряжение) и ни одному из электронов не удастся преодолеть задерживающее электрическое поле и достичь анода. Вольтамперная характеристика позволяет определить число электронов, вылетающих из катода в единицу времени и максимальную кинетическую энергию электронов, которая выражается через задерживающее напряжение. Коэффициент пропорциональности k (мкА/Вт), соответствующий силе фототока (выраженной в микроамперах) при освещенности катода световым потоком 1 Вт, называют фоточувствительностью элемента. Фототок насыщения I_н = е·n, где n — число электронов, испускаемых катодом в 1 с. Зависимость фототока насыщения от светового потока носит название световой характеристики фотоэлемента (Рис. 4).

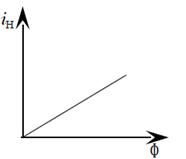
Рис.4 Световая характеристика фотоэлемента

Поскольку 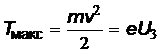, то уравнение Эйнштейна можно записать в виде:

.

В случае если энергия фотона много больше работы выхода ( ), то

Внешний фотоэффект считается состоявшимся, если электрон выходит из металла с нулевой скоростью. Максимальная длина волны 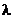падающего кванта или минимальная частота n₀, w₀, при которой это происходит, называется красной границей фотоэффекта.

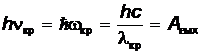
Красной граница фотоэффекта называется потому, что увеличение длины волны падающего света до максимально возможной соответствует смещению в сторону красной границы для видимого спектра. При меньшей частоте падающего света (большей длине волны) фотоэффект не наблюдается.

Энергию фотонов и работу выхода принято выражать во внесистемных единицах - электронвольтах (эВ). Один электронвольт равен энергии, приобретенной электроном при прохождении разности потенциалов 1В: 1 эВ = 1,6×10^-19 Дж.

Экспериментально было обнаружено, что зависимость 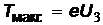от n для данного металла имеет вид наклонной прямой, причем наклон прямых, построенных для разных металлов, оказался одинаковым.

Из соотношения вытекает уравнение, соответствующее экспериментальной зависимости, показанной на Рис.5,

.

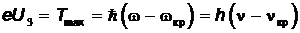Рис. 5 Зависимость максимальной кинетической энергии фотоэлектронов от частоты падающего света

Если электрон в металле является свободным (не связанным с атомом), то фотоэффект не состоится. Законы сохранения импульса и энергии для фотоэффекта в этом случае имели бы вид (до взаимодействия с фотоном электрон покоился):

,

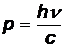
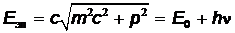где p – импульс электрона, - энергия покоя электрона; - энергия электрона, который после поглощения фотона приобрел импульс .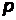

Возведя полученные соотношения в квадрат, получим

.

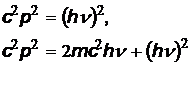При эти равенства несовместимы, откуда следует, что свободный электрон не может поглотить фотон.

Задача 1. Определите максимальную скорость фотоэлектронов, вырываемых с поверхности серебра:

1. ультрафиолетовым излучением с длиной волны 155 нм;

2. g - излучением с длиной волны 2,47 пм.

Работа выхода электрона из серебра равна 4,7 эВ.

Решение.Кинетическаяэнергия фотоэлектрона зависит от энергии фотона

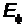, вызывающего фотоэффект. Если энергия фотона много меньше энергии покоя

электрона , то кинетическая энергия фотоэлектрона выражается по классической формуле , а если сравнима по величине или больше , то по релятивистской .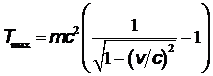

1. Энергия фотона 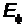равна:

Дж = 8 эВ,

что много меньше энергии покоя электрона 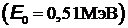. Поэтому максимальная кинетическая энергия фотоэлектрона выражается по классической формуле из уравнения Эйнштейна 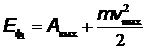, и равна

=1,08×10⁶м/с.

2. Энергия фотона g - излучения 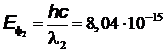Дж = 0,502 МэВ

сравнима с энергией покоя электрона, поэтому для вычисления его кинетической энергии необходимо использовать релятивистскую формулу. Работа выхода ( = 4,7 эВ) много меньше энергии g - фотона, поэтому ею можно пренебречь:

Выполнив преобразования, из уравнения Эйнштейна найдем

=0,755,

м/с.

Задача 2. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найдите длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.

Решение.Найдем длину волны из уравнения Эйнштейна .

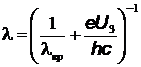= 196 нм.

Задача 3. Какую часть энергии фотона составляет энергия, которая пошла на совершение работы выхода электронов из металла, если длина волны для красной границы равна 0,54 мкм, а максимальная кинетическая энергия фотоэлектронов 0,5эВ?

Решение.Из формулы Эйнштейна для фотоэффекта 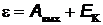получим 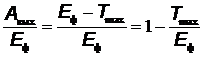, где 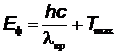= 4,48×10^-19 Дж = 2,8 эВ.

Тогда , то есть составляет 82%.

Задача 4. Возникает ли фотоэффект в цинке под действием излучения, имеющего длину волны 0,45 мкм? Работа выхода электронов из цинка равна 4,2 эВ.

Решение.Минимальная энергия кванта, вызывающего фотоэффект, равна работе выхода. Энергия кванта по условию задачи равна 2,75 эВ, что меньше работы выхода. Поэтому фотоэффекта не будет.

Задача 5. Металлический шар радиусом 10 см облучают светом с длиной волны 200 нм. Определите установившийся заряд шара, если работа выхода электрона с его поверхности равна 7,2×10^–19 Дж.

Решение. На шаре установится такой заряд, что под действием его электростатического поля самые быстрые электроны, покидающие поверхность шара вследствие фотоэффекта, вернутся на положительно заряженный шар. В этом случае вы

полняется равенство 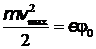, где 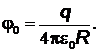Из уравнения Эйнштейна получим 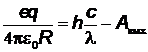, откуда

= 1,9×10^–11 Кл.

Задача 6. Фотоны с длиной волны 330 нм вырывают электроны из металла с работой выхода 2,9 эВ. Найдите максимальный импульс, передаваемый поверхности металла при вылете каждого электрона в результате фотоэффекта. Считать, что электрон вылетает нормально к поверхности катода навстречу падающему фотону.

Решение.Закон сохранения импульса для фотоэффекта имеет вид (рис.6):

_,

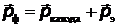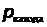
фотокатод

Рис.6

где – импульс фотона, 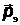– максимальный импульс электрона, 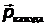– импульс, полученный поверхностью катода. Из уравнения Эйнштейна импульс падающего фотона

.

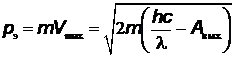Импульс, передаваемый поверхности, равен сумме импульса фотона и импульса вылетевшего фотоэлектрона.

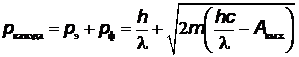= 5×10^–25 кг×м/с.

Давление света

Свет оказывает давление на освещаемую поверхность. Рассмотрим монохроматический световой поток частоты ν, падающий по нормали на плоскую поверхность площадью S с коэффициентом отражения ρ. По закону сохранения импульса относительно оси z, нормальной к поверхности

,

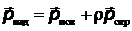где 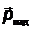- импульс падающего фотона с частотой ν ( 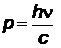), 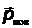- импульс, передаваемый фотоном поверхности, 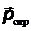- импульс отраженного фотона, ρ – коэффициент отражения. N фотонов передают поверхности импульс 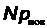. Число фотонов, падающих по нормали на поверхность за время Δt равно 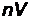, где n – число фотонов в единице объема, V – объем цилиндра площадью S и длиной сt, 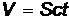. (Рис.7).

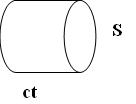
Рис.7

Импульс 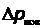, передаваемый поверхности световым потоком за время Δt, равен

,

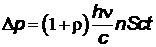а давление

,

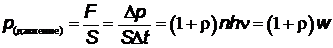где nhν – энергия фотонов в единичном объеме падающего светового потока, то есть плотность энергии w.

Примеры решения задач.

Задача 1.Определите, с какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 1) 0,55 мкм,

2) 1 пм.

Решение.Чтобы определить, является ли электрон классической или релятивистской частицей, энергию фотона 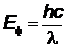следует сравнить с энергией покоя электрона 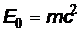. Вычислим соотношение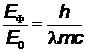

В первом случае получим 4,41·10^-6 , т.е. кинетическая энергия электрона много меньше его энергии покоя, и определяется по классической формуле: 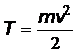. Тогда

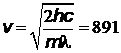м/с.

Во втором случае 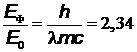, следовательно, кинетическая энергия электрона определяется релятивистской формулой:

.

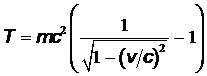Приравняв ее к энергии фотона 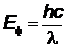, найдем

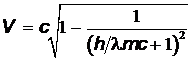= 2,87×10⁸ м/с.

Задача 2. Определите температуру, при которой средняя энергия молекул трехатомного газа равна энергии фотонов, соответствующих излучению с длиной волны 500 нм.

Решение. Средняя энергия молекулы 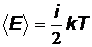,где 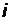- число степеней свободы, для трехатомного газа 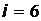. Энергия фотона .

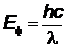Приравняв, эти энергии 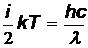, получим 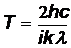= 9,6 кК.

Задача 3.Определите длину волны фотонов, импульс которого равен импульсу электрона, прошедшего разность потенциалов 10 В.

Решение. Кинетическая энергия электрона 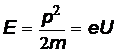, откуда его импульс 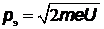. Приравняв его к импульсу фотона 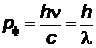, получим:

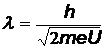= 388 пм.

Задача 4.Сколько фотонов испускает электрическая лампочка мощностью 25 Вт за время t = 1 с, если предположить, что вся потребляемая мощность идет на излучение монохроматического света с длиной волны 600 нм?

Решение.Энергия, потребляемая электрической лампочкой 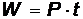равна энергии 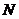испущенных фотонов 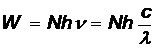, откуда число фотонов 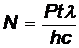= 7,54×10¹⁹.

Задача 5.Параллельный пучок света длиной волны 500 нм падает нормально на зачерненную поверхность, производя давление 10 мкПа. Определите концентрацию фотонов в пучке и число фотонов, падающих на поверхность площадью 1 м² за 1 с.

Решение.Концентрация 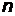фотонов в пучке может быть найдена из выраже-

ния для объемной плотности энергии :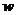

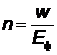, где 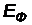- энергия одного фотона.

Из формулы, определяющей давление света, 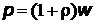, где r - коэффициент отражения, найдем

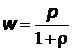, откуда .

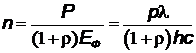Коэффициент отражения для зачерненной поверхности 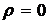, тогда

n = 2,52·10¹³м^-3. Число фотонов, падающих на поверхность единичной площади в единицу времени, выражается соотношением

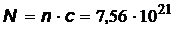м^-2·с^-1.

Эффект Комптона.

В 1922 году А. Комптон, исследуя рассеяние рентгеновского излучения различными веществами обнаружил, что в нем наряду с исходной длиной волны 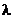появляется смещенная линия с длиной волны 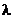¢ > 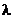(Рис.8).

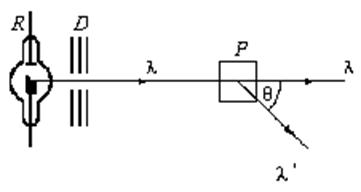
Рис.8 Схема установки по изучению эффекта Комптона

Это изменение длины волны получило название комптоновского смещения, а само явление эффекта Комптона. Комптоновское смещение 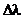не зависит от длины волны 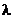и от природы рассеивающего вещества и определяется формулой:

,

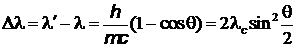где 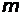– масса электрона или другой заряженной частицы, 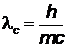- комптоновская длина волны этой частицы, l и l¢ - длины волн падающего и рассеянного излучения; q–угол рассеяния. Для электрона 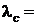2,42пм.

Все закономерности эффекта Комптона можно объяснить, если рассмотреть упругое столкновение рентгеновского кванта с покоящимся электроном, слабо связанным с атомом. Происходит процесс, напоминающий удар двух биллиардных шаров, когда один шар (рентгеновский квант) налетает на покоящийся шар (электрон) и в результате абсолютно упругого удара шары (рассеянный квант и электрон) разлетаются под некоторым углом. Налетающий квант с энергией 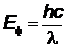передает часть своей энергии электрону, поэтому рассеянный квант имеет меньшую энергию и, следовательно, большую длину волны. Энергия рентгеновского кванта (десятки кэВ) на несколько порядков превосходит энергию связи электрона в атоме (десятки эВ), поэтому наиболее слабо связанные с атомом электроны внешних оболочек можно считать свободными и покоящимися.

Ядерная модель атома.

Экспериментально установив, что в атоме (размером ~10^–10м) имеется ядро (размером ~10^–15м), в котором сосредоточена вся масса атома (99,4%), Резерфорд предложил планетарную модель строения атома. Вокруг ядра с зарядом 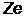( 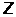–порядковый номер элемента в системе Д.И. Менделеева, е–заряд электрона) под действием сил электростатического притяжения по круговым (или эллиптическим) орбитам движутся электроны (подобно тому, как планеты обращаются вокруг Солнца под действием сил гравитационного притяжения), образуя электронную оболочку атома. Однако, такая модель оказалась несостоятельной. Движение электрона по круговой орбите происходит с нормальным ускорением, поэтому он постоянно излучает электромагнитные волны и теряет свою энергию. В результате через короткое время электрон упадет на ядро и атом перестанет существовать.

Выход из сложившейся ситуации предложил Нильс Бор, который дополнил модель атома Резерфорда двумя постулатами.

Постулаты Бора

Первый постулат Бора (постулат стационарных состояний):

В атоме существуют стационарные (не изменяющиеся со временем) орбиты (состояния), находясь на которых электрон не излучает электромагнитные волны.

Из всех возможных орбит электрона разрешенными являются только те, для которых момент импульса электрона кратен величине 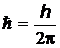, т.е. для которых выполняется условие (правило квантования):

( ),

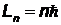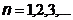где 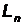–момент импульса электрона на 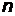- ой орбите, 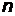- главное квантовое число, 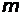–масса электрона, 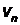–скорос