Определение перемещений с помощью интеграла Мора с использованием правила Верещагина
Для определения горизонтального перемещения рамы в сечении 1(сечение D) , выбираем единичное состояние – освободив раму от заданной нагрузки, прикладываем в сечении D сосредоточенную силу 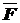 =1, направленную горизонтально (рис.39а).
=1, направленную горизонтально (рис.39а).
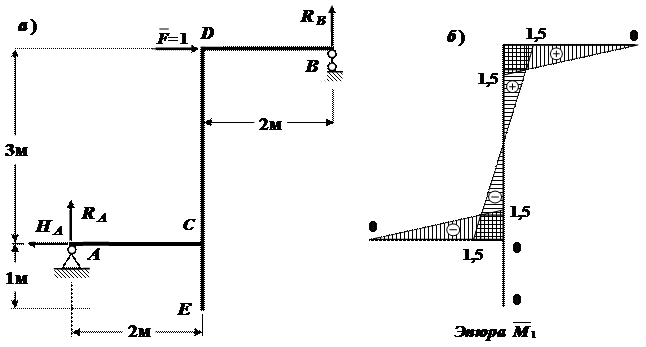
Рис.39. Эпюра изгибающих моментов от единичной сосредоточенной силы
 Определение опорных реакций. Составляем три уравнения статики (рис.39a):
Определение опорных реакций. Составляем три уравнения статики (рис.39a):
S Fx =0: 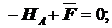
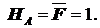
S MA =0: 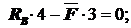
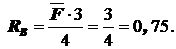
S MB=0: 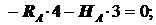 RA =
RA = 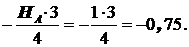
Проверка S Fz =0? RA + RB= – 0, 75 + 0, 75 = 0.
Значения изгибающих моментов.
Участок AC: 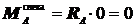 ;
; 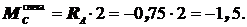
Участок BD: 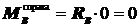 ;
; 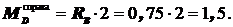
Поскольку участки CD и CE вертикальные разворачиваем раму на 900 по ходу часовой стрелки.
 Участок CD:
Участок CD: 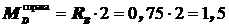 ;
; 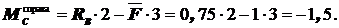
Участок CE: M ≡ 0.
Строим эпюру 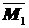 от единичного воздействия (рис.39б) и, не забываем проверить равновесие узлов C и D .
от единичного воздействия (рис.39б) и, не забываем проверить равновесие узлов C и D .
Горизонтальное перемещение рамы в сечении 1 по формуле Мора
v1= 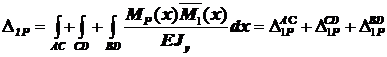
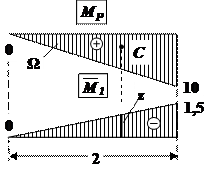 |
| Рис.40.Перемножение эпюр |
На участке АС (рис.40) площадь эпюры: 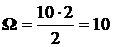 .
.
Ордината в эпюре 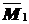 под центром тяжести равна:
под центром тяжести равна: 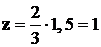 ; поэтому
; поэтому 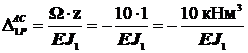 .
.
Такой же результат получится и для участка BD: 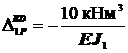 .
.
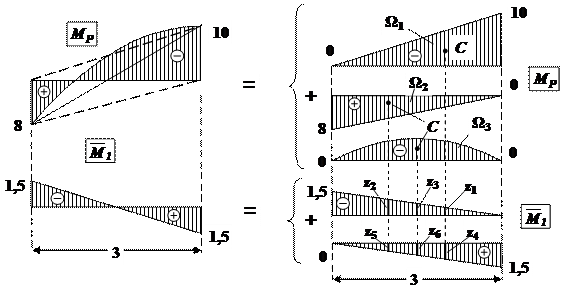
Эпюру от заданной нагрузки МР на участке CD, который развернем походу часовой стрелки, разбиваем на два треугольника и симметричную параболу, а эпюру 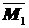 – на два треугольника (рис.41).
– на два треугольника (рис.41).
Площади этих эпюр: 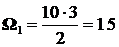 ;
; 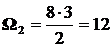
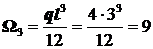 .
.
 Ординаты в эпюре
Ординаты в эпюре 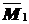 под центрами тяжести соответственно равны:
под центрами тяжести соответственно равны: 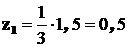 ;
; 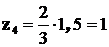 ;
; 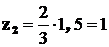 ;
; 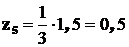 ;
; 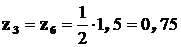 ; поэтому
; поэтому
Рис.41. Разбиение сложных эпюр на простые эпюры. Перемножение эпюр
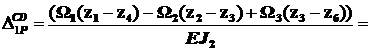
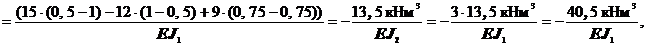
т.к. J2= J1/3.
Таким образом, горизонтального перемещения рамы в сечении 1
v1= 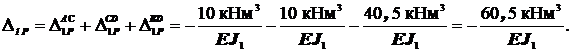
Отрицательное значение перемещения в сечении 1показывает, что рама в сечении 1 перемещается в направлении противоположном направлению единичной силы.
Для определения угла поворота рамы в сечении 2(сечение E) , выбираем единичное состояние – освободив раму от заданной нагрузки, прикладываем в сечении E сосредоточенный момент 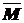 =1, направленный по ходу часовой стрелки (рис.42а).
=1, направленный по ходу часовой стрелки (рис.42а).
Определение опорных реакций. Составляем три уравнения статики:
 S Fx =0:
S Fx =0: 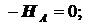
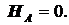
S MA =0: 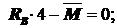
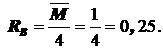
S MB=0: 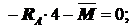 RA =
RA = 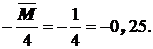
Проверка S Fz =0? RA + RB = – 0, 25 + 0, 25 = 0.
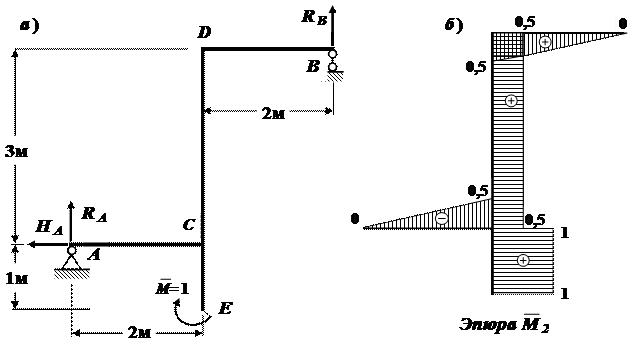
Рис.42.Эпюра изгибающих моментов от единичного сосредоточенного момента
 Значения изгибающих моментов.
Значения изгибающих моментов.
 Участок AC:
Участок AC: 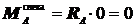 ;
; 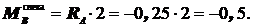
Участок BD: 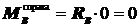 ;
; 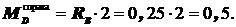
Поскольку участки CD и CE вертикальные разворачиваем раму на 900 по ходу часовой стрелки.
Участок CD: 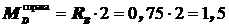 ;
; 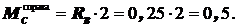
Участок CE: M ≡ 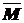 =1.
=1.
Строим эпюру 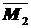 от единичного воздействия (рис.42б).
от единичного воздействия (рис.42б).
Интеграл Мора
j2= 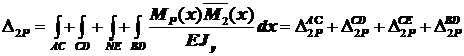 .
.
На участке АС (рис.32б) площадь эпюры: 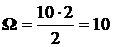 .
.
Ордината в эпюре 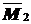 под центром тяжести равна:
под центром тяжести равна: 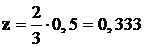 ; поэтому
; поэтому 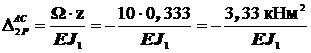 .
.
Такой же результат получится и для участка BD: 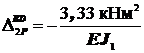 .
.
Эпюру от заданной нагрузки МР на участке CD, который развернем походу часовой стрелки, разбиваем на два треугольника и симметричную параболу, как это было сделано выше (рис.41).
Площади этих эпюр: 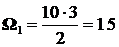 ;
; 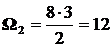 ;
; 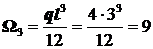 .
.
Ординаты в эпюре 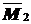 под центрами тяжести равны
под центрами тяжести равны 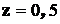 ; поэтому
; поэтому
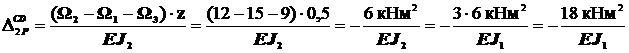 ,
,
т.к. J2= J1/3.
На участке CE (рис.33б) площадь эпюры: 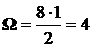 , а ордината в эпюре
, а ордината в эпюре 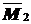 под центром тяжести равна
под центром тяжести равна 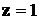 ; поэтому
; поэтому 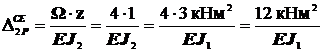 , т.к. J2= J1/3.
, т.к. J2= J1/3.
Таким образом, угол поворота рамы в сечении 2(сечение E)
j2 = 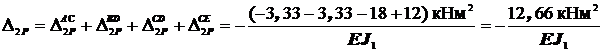 .
.
Отрицательное значение угла поворота рамы в сечении 2показывает, что сечение 2 поворачивается против хода часовой стрелки, т.е. в направлении противоположном направлению единичного момента.
Литература:
1. Дарков А. В. Строительная механика / А. В. Дарков, Н. Н. Шапошников. - СПб. : Издательство Лань, 2005. - 656 с.
2. Снитко Н. К. Строительная механика./ Н. К. Снитко – М. : Высшая школа, 1992. – 486 с.
3. Киселёв В. А. Строительная механика / В. А. Киселёв. - М. : Стройиздат, 1976. - 512 с.
