Задача 2. Определение перемещений в статически определимой балке

Для заданной схемы балки (рис.2) с размерами и нагрузкой, определяемыми по табл.2 требуется:

1. Выполнить кинематический анализ системы.

2. Построить поэтажную схему.

3. Построить эпюры изгибающих моментов(M) и поперечных сил (Q).

4.Определить перемещение (прогиб или угол поворота) в заданном сечении с помощью интеграла Мора с использованием правила Верещагина.

Первая цифра шифра	F, кН	l, м	Вторая цифра шифра	q, кН/м	№ сечения	Третья цифра шифра (№ схемы)	m, кНм	Вид переме-щения
								Угол поворота
				5,8				Угол поворота
				5,6				Угол поворота
				5,4				Угол поворота
				5,2				Угол поворота
				5,0				Прогиб
				4,8				Прогиб
				4,6				Прогиб
				4,4				Прогиб
								Прогиб

Таблица 2

Исходные данные

Замечание. Если сечение, в котором определяется угол поворота, совпадает с шарниром, тогда необходимо определить взаимный угол поворота примыкающих к шарниру сечений.

Рис.2. Схемы балок

Задача 3. Определение перемещений в статически определимой раме

Для заданной схемы статически определимой рамы (рис.3) с размерами и нагрузкой, определяемыми по табл.3 требуется:

1. Выполнить кинематический анализ системы.

2. Построить эпюры изгибающих моментов, поперечных и продольных сил.

3.Определить перемещение (прогиб или угол поворота) в заданном сечении с помощью интеграла Мора с использованием правила Верещагина.

Таблица 3

Исходные данные

Первая цифра шифра	F, кН	h, м	Вторая цифра шифра	q, кН/м	l, м	№ сечения	Третья цифра шифра (№ схемы)	m, кНм		Вид переме-щения
					4,2				1/2	Горизонтальное перемещение
	6,2	5,8		6,8	4,4				2/1	Вертикальное перемещение
	6,4	5,6		6,6	4,6				1/3	Горизонтальное перемещение
	6,8	5,4		6,4	4,8				3/1	Вертикальное перемещение
		5,2		6,2					2/3	Горизонтальное перемещение
	7,2				5,2				3/2	Угол поворота
	7,4	4,8		5,8	5,4				3/5	Угол поворота
	7,6	4,6		5,6	5,6				5/3	Угол поворота
	7,8	4,4		5,4	5,8				3/4	Угол поворота
		4,2							4/3	Угол поворота

Замечание.Поскольку в данной задаче жесткости отдельных стержней различны и заданы только их соотношения , искомые перемещения должны быть выражены через EJ₁ или EJ₂.

Рис.3. Схемы рам

I. Расчет статически определимой многопролетной балки

Статически определимая неизменяемая система,состоящая из рядабалок, с консолями или без консолей, соединенных между собой шарнираминазываетсястатически определимой многопролетной балкой(рис.4).

Рассмотрим основные этапы расчета многопролетной статически определимой балки.

Кинематический анализ

Степень статической определимости (неопределимости) определяется числом «лишних» связей по формуле S=3к – ш, где

к – число замкнутых контуров в конструкции в предположении отсутствия шарнирных соединений; ш– число одиночных шарниров.

Так для шарнирно - неподвижной опоры (опора D на рис.4) число одиночных шарниров –1, для шарнирно - подвижной опоры (например, опора A на рис.4) число одиночных шарниров –2. Для сложного шарнира ( ) число одиночных шарниров определяется по формуле ш = с–1, где с– число стержней, подходящих к шарниру. На рис.4 шарниры E и K – одиночные, т.к. к каждому из них подходит по два стержня.

Если S = 0 , то задача статически определимая. При S > 0 задача статически неопределимая, а при S < 0 – геометрически изменяемая.

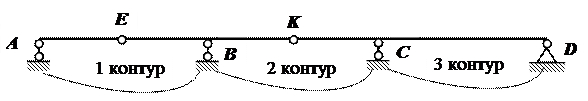Так на рис.4 балка имеет три замкнутых контура (к=3) и девять одиночных шарниров (ш =9), поэтому S=3к-ш= 3·3-9=0

Рис.4.Статически определимая многопролетная балка

Построение поэтажной схемы

Для удобства расчета и наглядности представления о характере работы отдельных частей многопролетной статически определимой балки строится её поэтажная схема. Для этого балка разрезается по промежуточным шарнирам и выделяются основные (их может быть одна или несколько) и подвесные балки.

Основной или главной является та балка, которая может самостоятельно нести внешнюю нагрузку после разрезания по промежуточному шарниру (балка KCD на рис.4). Все остальные балки являются подвесными или второстепенными(балки KBE и EA на рис.4).

Различают следующие типы многопролетных балок.

Первый тип характеризуется тем, что во всех пролетах, кроме одного (возможна и консоль), располагается по шарнирно-подвижной опоре. При замене шарниров на шарнирно неподвижные опоры получим однопролетные балки, каждая из которых опирается на консоль предыдущей ( рис.5а ).

Второй тип характеризуется чередованием пролетов, имеющих две

шарнирно-подвижные опоры, с безопорными. При этом в поэтажной схеме на консоли основных балок опираются балки-вставки. Для обеспечения статической определимости балок-вставок при замене шарниров на опоры один из них заменяется на шарнирно неподвижную опору, другой – на шарнирно подвижную опору. Если основная балка имеет две подвижные опоры, то одна из них заменяется на шарнирно неподвижную опору (рис.5б).

Рис.5.Многопролетные балки и их поэтажные схемы

Возможна и балка, совмещающая первый и второй типы (рис.6).

Рис.6. Многопролетная балка и её поэтажная схема