Уравнение частоты колебаний струны

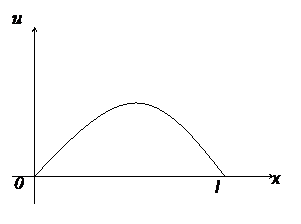Уравнение вида

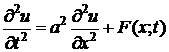(1)

с краевыми условиями

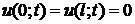(2)

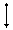и начальными условиями

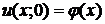(3)

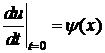(4)

описывает закон колебаний однородной тонкой нерастяжимой струны длины l, закрепленной на концах в точках х=0 и х=l (условия (2)), с начальной формой (х) (условие (3)) и начальной скоростью (х) (условие (4)), в поле действия внешней силы (например, силы тяжести, в магнитном поле и т.п.). Постоянный параметр a² зависит от свойств струны, функция F(x;t) - от внешней силы. Если F(x;t)=0 – это значит, что внешней силы нет (или ей можно пренебречь) и колебания называются свободными.

Отметим, что колебания рассматриваются малые (отклонение u точек струны от положения равновесия – оси Ох – мало), плоские (колебания происходят только в плоскости хOu), поперечные (каждая точка струны движется строго перпендикулярно положению равновесия).

Уравнение свободных колебаний струны, закрепленной на концах:

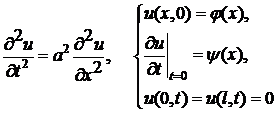
имеет решение вида

,

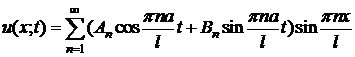где коэффициенты А_n и В_n находят из начальных условий:

подставляя t=0 получаем

,

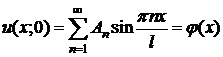то есть А_n – коэффициенты Фурье для функции (х) при разложении на интервале (0; l) по синусам кратных дуг.

Далее, дифференцируя u(х;t) по t и подставляя t=0 получаем:

,

то есть 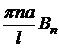– коэффициенты Фурье для функции (х) при разложении на интервале (0; l) по синусам кратных дуг.

Напомним, что коэффициенты Фурье в общем случае вычисляются при помощи интегралов (см. тему «Ряд Фурье», с.38), а иногда их можно подобрать (если раскладываемая функция представляет собой сумму синусов кратных дуг).

Фазовая скорость – это скорость распространения фазы волны.

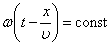
Зафиксируем какое-либо значение фазы волны и проследим, с какой скоростью фаза будет перемещаться вдоль оси x.

.

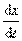
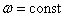
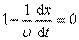Это уравнение дает связь между t и тем значением x, где зафиксированное значение фазы будет в данный момент времени. Следовательно, – это есть скорость перемещения данной фазы. Т.к. , поэтому .

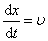Возьмем производную по времени от обеих частей равенства: . Отсюда получим выражение для фазовой скорости:

.

(5.3.1)

Итак, скорость распространения фазы есть скорость распространения волны. Т.е. υ в уравнении волны есть фазовая скорость. Для синусоидальной волны скорость переноса энергии равна фазовой скорости. Но синусоидальная волна не несет никакой информации, любой сигнал – это модулированная волна, т.е. несинусоидальная (негармоническая).

При решении некоторых задач получается, что фазовая скорость больше скорости света. Здесь нет парадокса, так как скорость перемещения фазы – это не скорость передачи(распространения) энергии, которая не может распространяться со скоростью большей, чем скорость света с.

Волновое уравнение.

Мы рассматриваем здесь газ или жидкость (так же как твердое тело в предыдущих параграфах) как сплошную непре­рывную среду, отвлекаясь от его атомистической структуры. Под смеще­нием 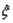мы здесь понимаем (как и в § 1) общее смещение вещества, запол­няющего объем, заключающий в себе очень много атомов, но малый по сравнению с длиной волны.

Будем считать, что рассматриваемый газ или жидкость находятся в очень длинной цилиндрической трубе, образующие которой парал­лельны оси х, и что смещение зависит только от одной координаты х. Мы можем применить к столбу газа или жидкости, заполняющему трубу, те же рассуждения, что и к стержню (§ 1). Мы придем, таким образом, к уравнению

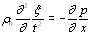(2.16)

где р = — 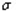есть давление в газе или жидкости. Здесь 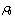— значение плот­ности в состоянии равновесия. Пусть ей соответствует давление р0. Ве­личины р0, 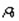не зависят ни от х, ни от t.

Уравнение (2.16) применимо и в случае плоских волн в неограничен­ной жидкой или газообразной среде (можно мысленно выделить цилин­дрический столб, параллельный направлению распространения и при­менить к нему те же рассуждения, что к столбу, заключенному в трубе).

Как известно из термодинамики, р есть функция плотности данной массы газа (или жидкости) и ее температуры. Температура в свою оче­редь изменяется при сжатии и разрежении. Теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями. В термодинамике показывается, что в этом случае (если можно пренебречь внутренним трением и некоторыми другими явлениями температура является однозначной функцией плотности , и следовательно, давление также.

При заданной деформации 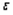в твердом теле также зависит от температуры. Но в акустике твердых тел это обстоятельство не играет, существенной роли.

В газах и в жидкостях за некоторыми исключениями (например вода, при температуре ниже 4° С) температура растет при сжатии и уменьшается при расшире­нии

Для газов и жидкостей, где звук распространяется обычно адиабатически (т. е. изменение температуры,связанное со сжатиями и разряжениями в звуковой волне, не успевает выравниваться за период), выражениедля С. з. можно представить, как

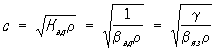
где Кад — адиабатический модуль объёмного сжатия, ρ — плотность, βад — адиабатическаясжимаемость, βиз = γβад — изотермическая сжимаемость, γ = cp/cv — отношение теплоёмкостей припостоянном давлении cp и при постоянном объёме cv.

В идеальном газе С. з.

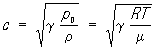
С. з. в газах меньше, чем в жидкостях, а в жидкостях меньше, как правило, чем в твёрдых телах, поэтомупри сжижении газа С. з. возрастает. С. з. в газах растет с ростом температуры и давления; в жидкостях С. з., как правило, уменьшается сростом температуры. Исключением из этого правила является вода, в которой С. з. увеличивается с ростомтемпературы и достигает максимума при температуре 74 °С, а с дальнейшим ростом температурыуменьшается. В морской воде (См. Морская вода) С. з. зависит от температуры, солёности и глубины, чтоопределяет ход звуковых лучей в море и, в частности, существование подводного звукового канала. С. з. в смесях газов или жидкостей зависит от концентрации компонентов смеси.

Энергия упругой волны Начнем рассмотрение вопроса об энергии упругой волны на примере простой модели продольной волны в одномерном кристалле (рис.2.1). Вычислим энергию, приходящуюся на один “элемент” нашего кристалла - один “атом” массой т и одну связь (пружину) с коэффициентом упругости k - см. рис.2.4. Кинетическая энергия элемента - это энергия “атома”, движущегося со скоростью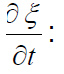

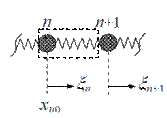
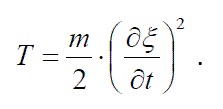
Потенциальная энергия деформирован- ной пружины пропорциональна квадрату величины её растяжения или сжатия (

учитывая соотношение (2.2), имеем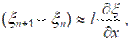

откуда

Итак, для рассматриваемой нами простой модели полная

энергия одного элемента одномерного кристалла: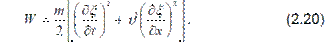

Эта формула может быть естественным образом обобщенана любые (не обязательно одномерные) среды с распределёнными параметрами. Для этого нужно только заменить массу одного элемента на массу, приходящуюся на единицу объёма среды (т.е. плотность ρ), при этом получим полную энергию, приходящуюся на единицу объёма среды, в которой распространяется упругая волна:

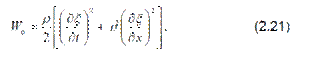
Величина W0 называется плотностью энергии упругой волны. Для плоской волны, распространяющейся по оси Х (как продольной, так и поперечной), зависимость смещения от координаты и времени определяется уравнением (2.8), откуда

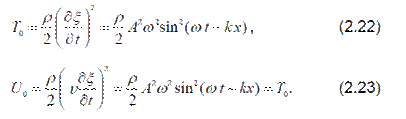
Из соотношений (2.22)–(2.23) получаем

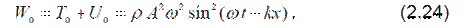
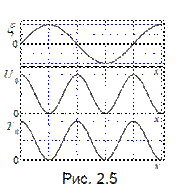На рис.2.5 показаны пространственное распределение ξ(х) и

соответствующие функции T0(x), U0(x) для бегущей упругой волны. Максимумы потенциальной и кинетической энергии в бегущей волне локализованы в одних и тех же местах (там, где ξ = 0). С течением времени показанная на рис.2.5 картинка “бежит” по оси Х со скоростью v. В любой фиксированной точке пространства величина плотности энергии со временем пульсирует (период пульсаций в два раза меньше периода волны – см. рис.2.5) Поэтому целесообразно определить среднее по времени (или в пространстве) значение плотности энергии 0W. Учитывая, что усреднение по времени квадрата синуса дает ½, получаем:

Поскольку волна переносит энергию, полезно определить несколько величин, характеризующих этот перенос.

Плотность потока энергии– количество энергии, переносимой волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Численно эта величина равна энергии, заключённой внутри цилиндрической поверхности с единичным основанием и образующей, равной v:

Подчеркнём, что плотность потока энергии является функцией времени, поскольку зависит от времени величина W₀(t) – см. (2.24).

Интенсивностью волныназывается среднее по времени значение плотности потока энергии волны:

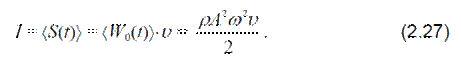
Русским физиком Н.А. Умовым в 1874 г. была введена векторная характеристика переноса энергии упругой волной:

Впоследствии величина Sr получила название вектора Умова. Как следует из (2.28), амплитуда вектора Умова изменяется со временем и в пространстве, поэтому целесообразно определить среднее по времени значение вектора Умова (векторную интенсивность волны):

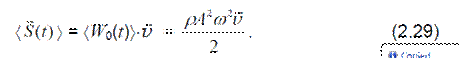
Поток энергии упругой волны через любую поверхность Σ можно определить интегрированием скалярного произведения вектора Умова на векторный элемент площадки srd (вектор srd направлен по нормали к площадке ds):

Здесь S_n – нормальная к площадке ds составляющая вектора Sr. Наконец, среднее по времени значение потока энергии упругой волны через поверхность:

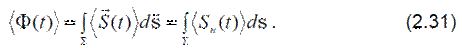
Эффе́кт До́плера —изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.

Сущность явления Эффект Доплера

Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится, и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты звуковых волн.

Для волн (например, звука), распространяющихся в какой-либо среде, нужно принимать во внимание движение как источника, так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, в вакууме имеет значение только относительное движение источника и приёмника

Математическое описание

Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны λ) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается:.

Где — круговая частота, с которой источник испускает волны, c — скорость распространения волн в среде, v — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником(1)
Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника(2)

где u — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

Подставив вместо в формуле (2) значение частоты из формулы (1), получим формулу для общего случая:(3)

Релятивистский эффект Доплера

В случае распространения электромагнитных волн (или других безмассовых частиц) в вакууме, формулу для частоты выводят из уравнений специальной теории относительности. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя

где c — скорость света, v — скорость источника относительно приёмника (наблюдателя), — угол между направлением на источник и вектором скорости в системе отсчёта приёмника. Если источник радиально удаляется от наблюдателя, то , если приближается — =Pi

Применение

· Доплеровский радар — радар, измеряющий изменение частоты сигнала, отражённого от объекта. По изменению частоты вычисляется радиальная составляющая скорости объекта (проекция скорости на прямую, проходящую через объект и радар). Доплеровские радары могут применяться в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков), морских и речных течений, а также других объектов.

· По увеличению ширины линий спектра можно измерить температуру фотосферы звёзд. Уширение линий при повышении температуры обусловлено увеличением скорости хаотического теплового движения излучающих или поглощающих атомов в газе.

Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует. (Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.)

Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны

и уравнения отраженной волны

Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме . После несложных преобразований, получаем

Это уравнение стоячей волны определяет смещение любой точки волны.

(1)

не зависит от времени и определяет амплитуду любой точки с координатой х. Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда Аст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в зависимости от расстояния х. Если придавать х значения, равные и т.д., то при подстановке в уравнение (1) получим

Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно

где λ - длина бегущей волны.

В стоячей волне все точки среды, в которой они распространяются, расположенные между двумя соседними узлами, колеблются в одной фазе. Точки среды, лежащие по разные стороны от узла, колеблются в противофазе -фазы их отличаются на π. т.е. при переходе через узел фаза колебаний скачкообразно меняется на π. В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная волны переносят энергию в равных количествах и в прямом и в противоположном направлениях. В том случае, когда волна отражается от среды более плотной, чем та среда, где распространяется волна, в месте отражения возникает узел, фаза изменяется на противоположную. При этом говорят, что происходит потеря половины волны. Когда волна отражается от среды менее плотной в месте отражения, появляется кучность, и потери половины волны нет.

Волновой пакет — определённая совокупность волн, обладающих разными частотами, которые описывают обладающую волновыми свойствами формацию, в общем случае ограниченную во времени ипространстве. Так, в квантовой механике описание частицы в виде волновых пакетов способствовало принятию статистической интерпретации квадрата модуля волновой функции.[1]

Произвольная отдельная волна как функция радиус-вектора и времени описывается выражением

где — мнимая единица, — энергия, переносимая волной, — редуцированная постоянная Планка, — импульс, переносимый волной, — её «круговая» частота (обычная частота, умноженная на ), — волновое число (определяемое как ; здесь скорость света).

Для волнового описания отдельной частицы, обладающей массой покоя, необходимо просуммировать некоторое количество волн, обладающих близкими частотами,— и в таком случае волновая функция будет заметно отлична от нуля лишь в некоторой, сравнительно небольшой области пространства. Получится волновой пакет.

Образуем волновой пакет из суперпозиции (набора) плоских волн, для которых волновое число изменяется от до (для простоты предположим, что на имеющем основное значение интервале амплитуды остаются постоянными и равными ):

где теперь обозначает результирующую волновую функцию, а величины обозначают вклады волн , из которых образован пакет, в результирующую волну, причем .

Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скоростьперемещения максимума амплитудной огибающейквазимонохроматического волнового пакета (или цуга волн). В случае рассмотрения распространения волн в пространстве размерностью больше единицы подразумевается как правило волновой пакет близкий по форме к плоской волне[1].

Групповая скорость во многих важных случаях определяет скорость переноса энергии и информации квазисинусоидальной волной (хотя это утверждение в общем случае требует серьёзных уточнений и оговорок).

Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно).

Для одномерных волн групповая скорость вычисляется из закона дисперсии:

,где — угловая частота, — волновое число.

Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентом частоты по волновому вектору:

или (для трехмерного пространства):

Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора.

Частные случаи

В одномерных средах без дисперсии групповая скорость формально совпадает с фазовой скоростью лишь в случае одномерных волн.

В диссипативных (поглощающих) средах групповая скорость уменьшается с увеличением частоты в случае нормальной дисперсии фазовой скорости и, наоборот, увеличивается в средах саномальной дисперсией.

Если дисперсионные свойства среды таковы, что волновой пакетраспространяется в ней без существенных изменений формы своей огибающей, групповая скорость обычно может быть интерпретирована как скорость переноса «энергии» волны и скорость, с которой могут быть переданы с помощью волнового пакета сигналы, несущие информацию, (то есть «скорость распространения причинности»).

В классическом пределе квантовомеханических уравнений скорость классической частицы представляет собой значение групповой скорости соответствующей квантовомеханической волновой функции. Одно из пары канонических уравнений Гамильтона:

— есть, таким образом, классический предел приведенного выше выражения для групповой скорости; это особенно ясно в декартовых координатах, учитывая