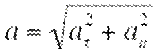Нормальное и тангенциальное ускорение
|
| 2.Законы Ньютона |
Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем.
Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению. Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инертностью. Поэтому первый закон Ньютона называют законом инерции. Масса тела – количественная мера инертности тела. В СИ масса тела измеряется в килограммах.
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Системы отсчета, движущиеся относительно инерциальных с ускорением, называются неинерциальными. Сила – количественная мера взаимодействия тел. Сила – векторная величина. В СИ сила измеряется в ньютонах (Н). Если на тело действует несколько сил, то их векторная сумма называется равнодействующей этих сил.
Второй закон Ньютона. Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:
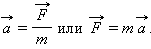 |
Если два тела взаимодействуют друг с другом, то ускорения этих тел обратно пропорциональны их массам.
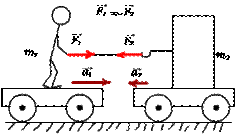 |
Третий закон Ньютона. Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона(закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действиеэтих сил компенсируется) движутся прямолинейно и равномерно или покоятся.
Всякая система отсчёта, движущаяся относительно ИСО равномерно и прямолинейно, также являетсяИСО. Согласно принципу относительности, все ИСО равноправны, и все законы физики инвариантныотносительно перехода из одной ИСО в другую. Это значит, что проявления законов физики в них выглядятодинаково, и записи этих законов имеют одинаковую форму в разных ИСО.
2.Закон сохранения импульса
Из второго и третьего законов Ньютона вытекает закон сохранения импульса замкнутой системы.
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.
Рассмотрим изолированную механическую систему, состоящую из n тел с массами m1, m2, …, mn. Обозначим скорости этих тел через v1, v2, …, vn а внутреннюю силу, действующую на i-е тело со стороны k-го,- через Fik.
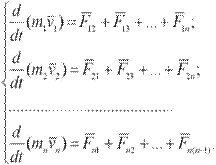 Складывая почленно эти уравнения и группируя силы Fik и Fki, получим:
Складывая почленно эти уравнения и группируя силы Fik и Fki, получим:
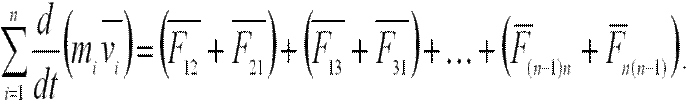
Согласно третьему закону Ньютона Fik = -Fki, поэтому все скобки в правой части этого уравнения равны нулю, т.е.
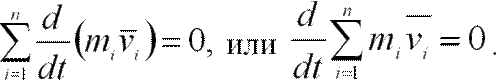
Векторная сумма 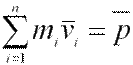 представляет собой импульс всей системы. Таким образом,
представляет собой импульс всей системы. Таким образом, 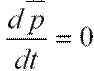 или
или
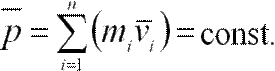 (2.9)
(2.9)
Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.
Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и являетсяфундаментальным законом природы.
Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета.
В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс.
Скорость i-й материальной точки связана с ее радиусом-вектором ri соотношением:
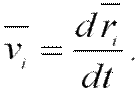
Следовательно,
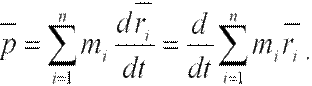
Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
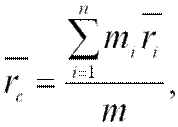
где 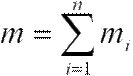 масса системы.
масса системы.
Скорость центра масс определяется выражением:
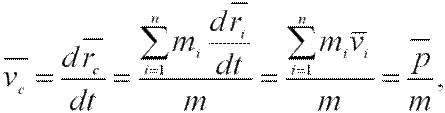
т.е.
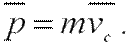 (2.10)
(2.10)
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции.
Подставив выражение (2.10) в (2.9), получим:
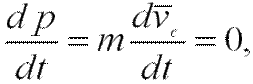
т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно.
Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом:
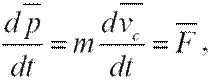
или
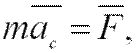 2.11)
2.11)
где 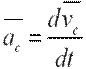 ускорение центра масс.
ускорение центра масс.
Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
4.Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов 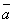 ,
, 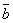 обозначается символом
обозначается символом 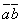 (порядок записи сомножителей безразличен, то есть
(порядок записи сомножителей безразличен, то есть 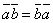 ).
).
Если угол между векторами 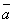 ,
, 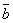 обозначить через
обозначить через 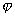 , то их скалярное произведение можно выразить формулой
, то их скалярное произведение можно выразить формулой
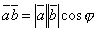 (1)
(1)
Скалярное произведение векторов 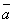 ,
, 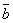 можно выразить также формулой
можно выразить также формулой
a · b = ax · bx + ay · by
Из формулы (1) следует, что 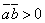 , если
, если 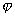 - острый угол,
- острый угол, 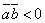 , если
, если 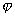 - тупой угол;
- тупой угол; 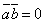 в том и только в том случае, когда векторы
в том и только в том случае, когда векторы 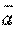 и
и 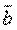 перпендикулярны (в частности,
перпендикулярны (в частности, 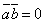 , если
, если 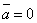 или
или 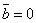 ).
).
Скалярное произведение 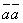 называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом 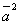 . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
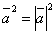 .
.
Если векторы 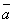 и
и 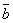 заданы своими координатами:
заданы своими координатами:
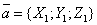 ,
,  ,
,
то их скалярное произведение может быть вычислено по формуле
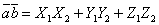 .
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
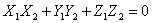 .
.
Угол 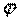 между векторами
между векторами
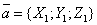 ,
,  ,
,
дается формулой 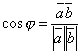 , или в координатах
, или в координатах
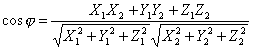 .
.
Проекция произвольного вектора 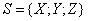 на какую-нибудь ось u определяется формулой
на какую-нибудь ось u определяется формулой
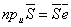 ,
,
где 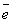 - единичный вектор, направленный по оси u. Если даны углы
- единичный вектор, направленный по оси u. Если даны углы 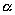 ,
, 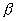 ,
, 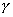 , которые оси u составляет с координатными осями, то
, которые оси u составляет с координатными осями, то 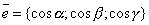 и для вычисления вектора
и для вычисления вектора 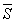 может служить формула
может служить формула
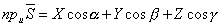 .
.
5 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ СИСТЕМЫ
3.1. Кинетическая энергия материальной системы
Кинетическая энергия системы складывается из кинетической энергии отдельных точек и тел, входящих в систему.
Кинетическая энергия точки массой 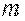 , движущейся со скоростью
, движущейся со скоростью 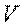 ,
,
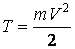 . (3.1)
. (3.1)
Кинетическая энергия твердого тела вычисляется по формулам:
● при поступательном движении
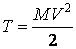 , (3.2)
, (3.2)
где 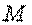 – масса тела;
– масса тела; 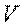 – скорость какой-либо точки тела (при поступательном движении тела скорости всех точек одинаковы);
– скорость какой-либо точки тела (при поступательном движении тела скорости всех точек одинаковы);
● при вращении вокруг неподвижной оси
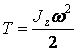 . (3.3)
. (3.3)
где 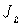 – момент инерции тела относительно оси вращения;
– момент инерции тела относительно оси вращения; 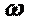 – угловая скорость тела;
– угловая скорость тела;
● при плоскопараллельном движении
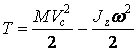 , (3.4)
, (3.4)
где 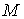 – масса тела;
– масса тела; 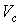 – скорость центра масс;
– скорость центра масс; 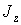 – момент инерции относительно оси
– момент инерции относительно оси 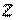 , проходящей через центр масс
, проходящей через центр масс 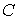 перпендикулярно плоскости движения;
перпендикулярно плоскости движения; 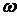 – угловая скорость тела.
– угловая скорость тела.
В системе с одной степенью свободы скорости разных точек и угловые скорости тел в формулах (3.1)–(3.4) выражаются через одну какую-либо скорость. Для этого надо учитывать известные кинематические зависимости между скоростями в движущихся системах.
Вычислим кинетическую энергию системы, изображенной на рис. 3.1, выразив скорости всех тел через скорость центра масс 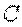 тела 2. Тела 1 и 2представляют собой однородные круглые цилиндры массой
тела 2. Тела 1 и 2представляют собой однородные круглые цилиндры массой 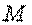 и радиусом
и радиусом  ; цилиндр 1 вращается вокруг оси
; цилиндр 1 вращается вокруг оси 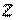 , а цилиндр 2 катится без проскальзывания по рельсу.
, а цилиндр 2 катится без проскальзывания по рельсу.

Рис. 3.1
Кинетическая энергия тела 1 определяется по формуле (3.3), а тела 2 – по формуле (3.4). Учтем, что 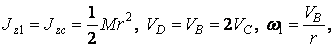
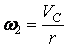 .
.
В результате имеем:
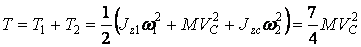 .
.
3.2. Работа силы
Работа сил, действующих на систему, определяет изменение кинетической энергии системы (см. подразд. 3.3).
Работой силы на заданном отрезке траектории перемещения точки приложения силы называется криволинейный интеграл по этому отрезку от скалярного произведения вектора силы на вектор элементарного перемещения точки.
Рассмотрим наиболее характерные случаи вычисления работы силы.
3.2.1. Работа постоянной силы на прямолинейном перемещении
Работа постоянной силы 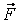 на прямолинейном перемещении точки приложения силы равна произведению трех величин: модуля силы
на прямолинейном перемещении точки приложения силы равна произведению трех величин: модуля силы 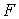 , пройденного точкой пути
, пройденного точкой пути 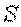 и косинуса угла между направлением вектора
и косинуса угла между направлением вектора 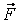 и направлением перемещения точки, т. е.
и направлением перемещения точки, т. е.
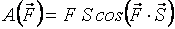 . (3.5)
. (3.5)
Отметим частные случаи:
● сила 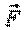 и направление перемещения точки приложения силы совпадают
и направление перемещения точки приложения силы совпадают
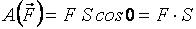 ;
;
● сила 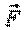 противоположна направлению перемещения точки
противоположна направлению перемещения точки
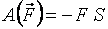 ;
;
● сила 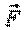 перпендикулярна перемещению точки
перпендикулярна перемещению точки
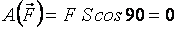 .
.
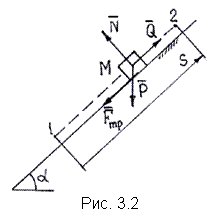 | Определим работу постоянных сил 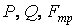 и и 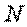 (рис. 3.2) при перемещении тела (рис. 3.2) при перемещении тела 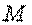 вверх по наклонной плоскости на расстояние вверх по наклонной плоскости на расстояние 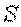 . По формуле (3.5) найдем . По формуле (3.5) найдем 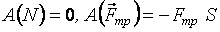 ; ; 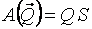 ; ; 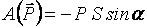 . . |
3.2.2. Работа силы тяжести
Работа силы тяжести равна взятому со знаком “плюс” или “минус” произведению силы тяжести 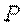 на высоту
на высоту 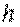 подъема или опускания точки приложения силы
подъема или опускания точки приложения силы 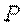 , т. е.
, т. е.
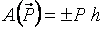 , (3.6)
, (3.6)
знак “плюс” соответствует опусканию, “минус” – подъему точки приложения силы 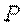 .
.
Следует подчеркнуть, что работа силы тяжести не зависит от вида траектории, по которой перемещается точка приложения силы. Определим работу силы тяжести шарика на участке 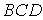 траектории, изображенной на рис. 3.3. Эта работа по формуле (3.6) определяется как траектории, изображенной на рис. 3.3. Эта работа по формуле (3.6) определяется как 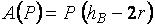 , здесь , здесь 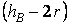 – смещение шарика по вертикали на участке – смещение шарика по вертикали на участке 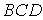 траектории. 3.2.3. Работа постоянного крутящего момента, приложенного к вращающемуся телу траектории. 3.2.3. Работа постоянного крутящего момента, приложенного к вращающемуся телу | 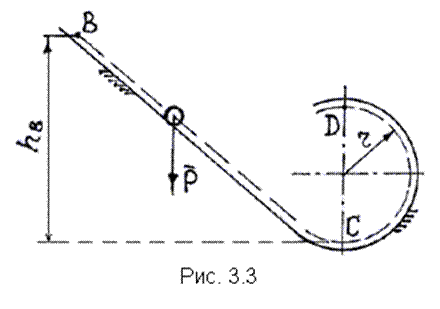 |
Работа крутящего момента 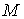 равна взятому со знаком “плюс” или “минус” произведению момента на угол поворота тела
равна взятому со знаком “плюс” или “минус” произведению момента на угол поворота тела 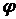 , т. е.
, т. е.
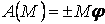 . (3.7)
. (3.7)
Знак “плюс” принимают в случаях, когда действие момента совпадает с направлением вращения тела, знак “минус” – когда это действие противоположно направлению вращения. Определим работу постоянного момента 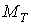 , вызывающего остановку маховика(рис. 3.4), если за время действия момента , вызывающего остановку маховика(рис. 3.4), если за время действия момента 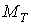 маховик сделал маховик сделал 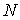 оборотов до остановки. По формуле (3.7) имеем оборотов до остановки. По формуле (3.7) имеем 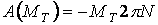 . Здесь учтено, что угол поворота тела . Здесь учтено, что угол поворота тела 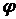 за за 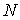 оборотов равен оборотов равен 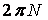 радиан. 3.2.4. Работа постоянной силы, приложенной к телу, совершающему плоскопараллельное движение радиан. 3.2.4. Работа постоянной силы, приложенной к телу, совершающему плоскопараллельное движение | 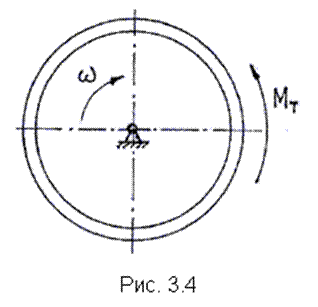 |
В данном случае силу вначале надо привести к центру масс тела, т. е. эту силу надо перенести параллельно самой себе в центр масс и добавить присоединенную пару сил, момент которой равен моменту заданной силы относительно центра масс. Затем по формуле (3.5) вычислить работу силы, приложенной к центру масс, и по формуле (3.7) вычислить работу момента присоединенной пары сил. Алгебраическая сумма этих работ и есть работа заданной силы.
Определим работу силы 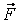  , постоянно приложенной в верхней точке , постоянно приложенной в верхней точке 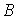 колеса (рис. 3.5), при перемещении центра колеса на расстояние колеса (рис. 3.5), при перемещении центра колеса на расстояние 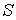 . Колесо катится по прямому рельсу без проскальзывания, поэтому . Колесо катится по прямому рельсу без проскальзывания, поэтому 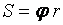 . Согласно предложенному правилу вычисления работы имеем . Согласно предложенному правилу вычисления работы имеем 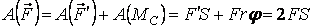 . 3.2.5. Работа постоянной силы трения при скольжении . 3.2.5. Работа постоянной силы трения при скольжении | 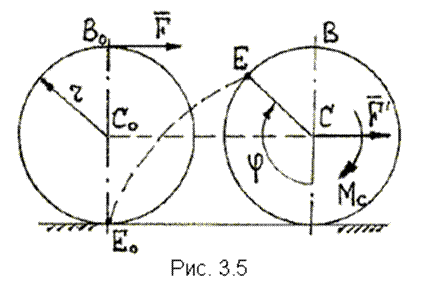 |
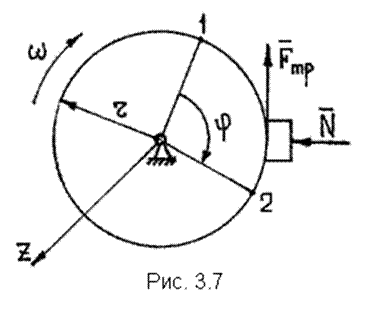
Работа постоянной силы трения при скольжении определяется так же, как и работа любой постоянной силы (см. п. 3.2.1). к поступательно движущемуся телу (рис. 3.6), то согласно формуле (3.5) ее работа 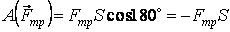 . По закону Кулона . По закону Кулона 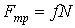 , где , где 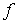 – коэффициент трения; – коэффициент трения; 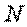 – нормальная реакция плоскости – нормальная реакция плоскости 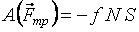 . (3.8) Если сила трения приложена к вращающемуся телу (рис. 3.7), то вначале следует определить момент этой силы относительно оси вращения . (3.8) Если сила трения приложена к вращающемуся телу (рис. 3.7), то вначале следует определить момент этой силы относительно оси вращения 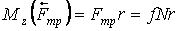 , а затем вычислить работу этого момента по формуле (3.7): , а затем вычислить работу этого момента по формуле (3.7): 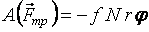 , где , где 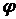 – угол поворота тела. 3.2.6. Работа постоянных сил трения при качении колеса по неподвижному основанию без проскальзывания В точке – угол поворота тела. 3.2.6. Работа постоянных сил трения при качении колеса по неподвижному основанию без проскальзывания В точке 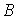 колеса действует сила трения скольжения колеса действует сила трения скольжения 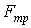 и момент трения качения и момент трения качения 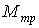 (рис. 3.8). Работа силы трения скольжения равна нулю, так как скорость точки (рис. 3.8). Работа силы трения скольжения равна нулю, так как скорость точки 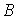 всегда равна нулю. Работа момента трения всегда равна нулю. Работа момента трения 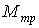 определяется по формуле (3.7) определяется по формуле (3.7) | 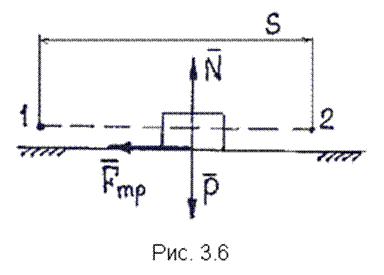 |
 |
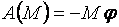 . (3.9)
. (3.9)
Известно, что 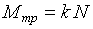 , где , где 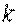 – коэффициент трения качения; – коэффициент трения качения; 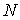 – нормальная реакция плоскости. Угол – нормальная реакция плоскости. Угол 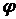 поворота колеса определяется по известной из кинематики формуле поворота колеса определяется по известной из кинематики формуле 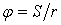 , где , где 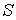 – путь, пройденный центром – путь, пройденный центром 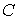 колеса. Подставляя эти результаты в (3.9), получим колеса. Подставляя эти результаты в (3.9), получим 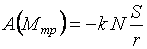 . 3.2.7. Работа переменной силы на прямолинейном перемещении Рассмотрим случай, когда точка . 3.2.7. Работа переменной силы на прямолинейном перемещении Рассмотрим случай, когда точка 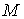 (рис. 3.9) движется в положительном направлении оси (рис. 3.9) движется в положительном направлении оси 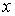 , а сила , а сила 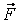 действует вдоль этой оси и является некоторой функцией координаты действует вдоль этой оси и является некоторой функцией координаты 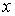 точки. точки. | 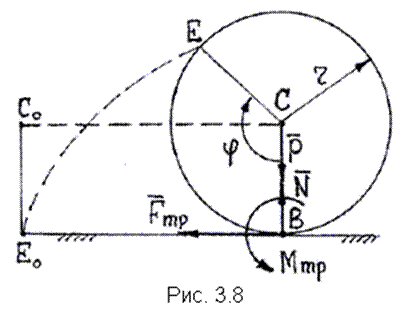 |
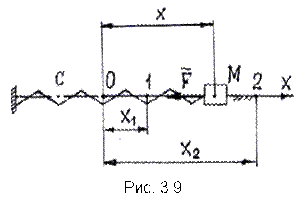 | Работа силы 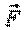 при перемещении точки из положения 1 в положение 2 определяется по формуле при перемещении точки из положения 1 в положение 2 определяется по формуле 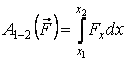 , (3.10) где , (3.10) где 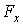 – проекция силы – проекция силы 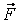 на ось на ось 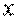 (на рис. 3.9 (на рис. 3.9 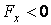 ), ), 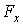 – заданная функция координаты – заданная функция координаты 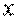 . Например, . Например, 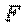 – сила упругости пружины, изменяющаяся по закону – сила упругости пружины, изменяющаяся по закону 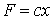 , , |
где 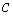 – коэффициент жесткости;
– коэффициент жесткости; 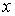 – деформация пружины и одновременно координата точки приложения силы
– деформация пружины и одновременно координата точки приложения силы 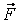 (рис. 3.9). Начало оси
(рис. 3.9). Начало оси 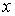 совпадает с концом недеформированной пружины.
совпадает с концом недеформированной пружины.
Формула (3.10) в этом случае после интегрирования дает результат:
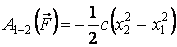 .
.
3.2.8. Работа переменного момента, приложенного к вращающемуся телу
Работа момента 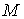 , являющегося некоторой функцией угла поворота тела (рис. 3.10), при повороте тела из положения 1, определяемого углом
, являющегося некоторой функцией угла поворота тела (рис. 3.10), при повороте тела из положения 1, определяемого углом 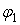 , в положение2, определяемое углом
, в положение2, определяемое углом 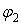 , вычисляется по формуле
, вычисляется по формуле
 | |
| 6 Консервативные силы и системы | |
Кроме контактных взаимодействий, наблюдаются взаимодействия между телами, удаленными друг от друга. Подобное взаимодействие осуществляется посредством физических полей (особая форма материи). Каждое тело создает вокруг себя поле, которое проявляет себя именно воздействием на другие тела.
Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и конечного положения тела, называются консервативными.
Обозначим A – работа консервативных сил, по перемещению тела из точки 1 в точку 2 (рис. 5.2).

Рис. 5.2. A 1a2 = A 1b2 = A 1l2 = A 12
Изменение направления движения на противоположное вызывает изменение знака работы консервативных сил. Отсюда следует, что работа консервативных сил вдоль замкнутой кривой равна нулю:
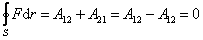 ,
,
Интеграл по замкнутому контуру S 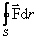 называется циркуляцией вектора
называется циркуляцией вектора 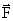 . Следовательно, если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна.
. Следовательно, если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна.
Консервативные силы: сила тяжести, электростатические силы, силы центрального стационарного поля.
Неконсервативные силы: силы трения, силы вихревого электрического поля.
Консервативная система – такая, внутренние силы которой только консервативные, внешние – консервативны и стационарны.
Пример консервативных сил – гравитационные силы (рис. 5.3).
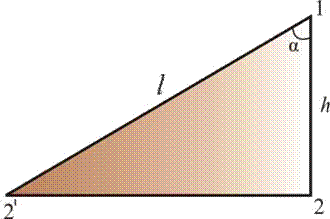
Рис. 5.3
Работа по подъему тела массы m на высоту h равна: 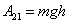 .
.
С другой стороны, 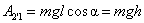 , где α – угол между силой и направлением перемещения.
, где α – угол между силой и направлением перемещения.
Таким образом, из примера видно, что работа не зависит от формы пути, значит, силы консервативны, а поле этих сил потенциально.
Потенциальная энергия
Если на систему материальных тел действуют консервативные силы, то можно ввести понятие потенциальной энергии.
Работа, совершаемая консервативными силами при изменении конфигурации системы, то есть при изменении положения тел относительно системы отсчета, не зависит от того, как было осуществлено это изменение. Работа определяется только начальной и конечной конфигурациями системы.
A12 = U1 – U2.
(5.3.1)
Здесь потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат всех тел системы в поле консервативных сил.
Итак, K определяется скоростью движения тел системы, а U – их взаимным расположением.
Из (5.3.1) следует, что работа консервативных сил равна убыли потенциальной энергии:
dA = – dU.
Нет единого выражения для U. В разных случаях она определяется по-разному.
7 Закон сохранения механической энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменениюпотенциальной энергии тел, взятому с противоположным знаком:
A = –(Eр2 – Eр1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19):
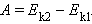
Следовательно
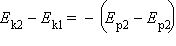 или
или
Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.
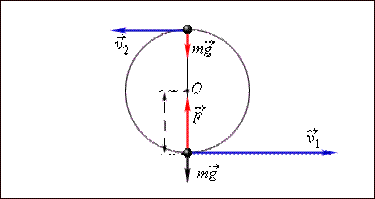
Рисунок 1.20.1.
К задаче Христиана Гюйгенса. 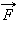 – сила натяжения нити в нижней точке траектории
– сила натяжения нити в нижней точке траектории
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
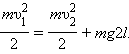
Обратим внимание на то, что сила 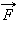 натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
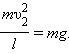
Из этих соотношений следует:
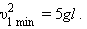
Центростремительное ускорение в нижней точке создается силами 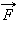 и
и 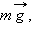 направленными в противоположные стороны:
направленными в противоположные стороны:
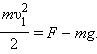
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
F = 6mg.
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.20.2).
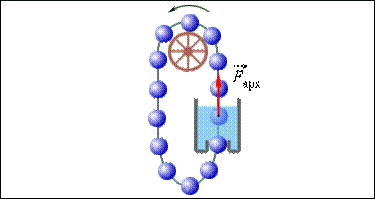
Рисунок 1.20.2.7гт
Один из проектов «вечного двигателя». Почему эта машина не будет работать?
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
 |

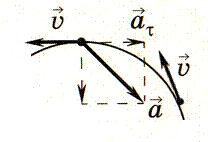 Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением
Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением 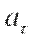 . Она характеризует изменение скорости по модулю.
. Она характеризует изменение скорости по модулю. 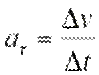 Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением 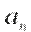 . Она характеризует изменение скорости по направлению.
. Она характеризует изменение скорости по направлению. 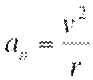 Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
Здесь R - радиус кривизны траектории в данной точке. Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения