Скорость и ускорение при гармонических колебаниях.

Согласно определению скорости, скорость – это производная от координаты по времени

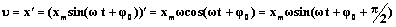
Xm=A

Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.

Величина 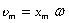- максимальная скорость колебательного движения (амплитуда колебаний скорости).

Следовательно, для скорости при гармоническом колебании имеем: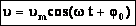

а для случая нулевой начальной фазы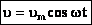

Согласно определению ускорения, ускорение – это производная от скорости по времени: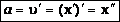

вторая производная от координаты по времени. Тогда: .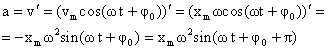

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).

Величина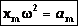

- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,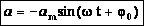

а для случая нулевой начальной фазы: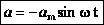

Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).

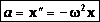
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.

Часто бывает удобно записывать уравнения для колебаний в виде: ,

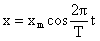
где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться.

Билет 16) Физический маятник (лаб.). Приведенная длина физического маятника

ФИЗИЧЕСКИЙ МАЯТНИК

Цель работы – изучение физического маятника, определение ускорения свободного падения.

Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.

Краткая теория

Физический маятник – твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной оси O(рис. 1).

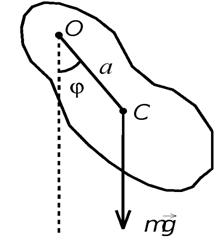
Рис. 1. Физический маятник

Запишем основное уравнение динамики вращательного движения.

.

I β = М ,(1)

где I – момент инерции маятника;

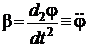– угловое ускорение, φ – угол отклонения маятника от положения равновесия, М - сумма проекций моментов сил на направление оси вращения. Если момент сил трения много меньше момента силы тяжести, то

M= -mga×sinj ,, (2)

где т– масса маятника, g –- ускорение свободного падения, а –- расстояние от оси вращения до центра тяжести.

Уравнение движения (1) с учетом (2) примет вид

Ij = -mga×sinα

где ω_о² = (mga)/I ,тогда получим уравнение:

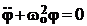. (3)

Уравнение (3) является линейным дифференциальным уравнением относительно функции φ(t).

Если амплитуда колебаний физического маятника не мала, дифференциальное уравнение (3) не будет линейным. Для больших углов отклонений маятника период Т начинает зависеть от амплитуды колебаний φ_{m .} Эту зависимость можно представить суммой бесконечного ряда, первые слагаемые которого равны

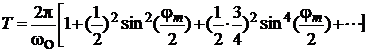. (4)

При малых колебаниях угол φ мал, поэтому sinφ ≈ φ и уравнение (3) становится дифференциальным уравнением гармонических колебаний

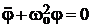. (5)

Решение этого уравнения:

j = j_mcos(ω₀t + α), (6)

где α - начальная фаза колебаний, ω_о = 2π/Т - циклическая частота колебаний.

Запишем формулу периода малых колебаний, как

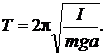(7)

Получим зависимость периода малых колебаний от расстояния а. Момент инерции, согласно теореме Штейнера, равен

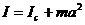, (8)

где I_с - момент инерции маятника относительно оси, проходящей через центр масс. Подставляя (8) в (7), получим

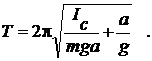(9)

Согласно этой формуле период колебаний Т одинаков при двухразличных значениях а (рис. 2): Т₁ = Т₂ при

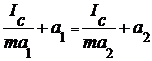, откуда

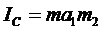. (10)

Подставим (10) в формулу (9). Получим

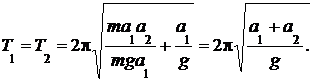(11)

Величина 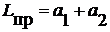(12)

называется приведенной длиной физического маятника.

Сравнивая формулы (11) и (7) получим

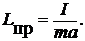(13)

Формула для периода малых колебаний маятника будет иметь следующий вид

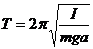. (14)

В данной работе с помощью физического маятника находится ускорение свободного падения g,которое исходя из уравнения (14),

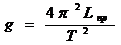. (15)

Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника.

Приведенная длина 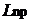находится из формулы (12), в которой а₁и а₂определяются из графика зависимости Т от а, построенного на основе результатов эксперимента.

Для уменьшения погрешности измерения в эксперименте измеряют период колебаний маятника относительно осей, находящихся по обе стороны от центра тяжести. На рис. 2 представлена теоретическая зависимость периода колебаний от параметра a, которая зеркально симметрична относительно оси Т.

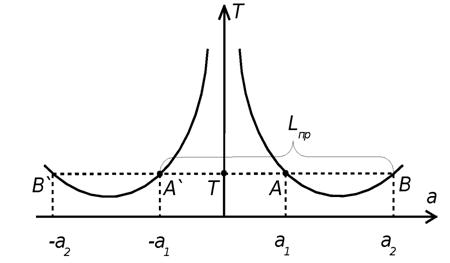Рис. 2. Зависимость периода колебаний маятника от параметрa a

На рисунке приведенная длина маятника L_np = a_{1 +} a₂ равна расстоянию между точками А ̀В или В̀ А.