Основной закон динамики вращательного движения

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела

, (1.6)

где F – сила, приложенная к телу массой m; а – линейное ускорение тела.

Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение 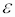и соответственные линейные ускорения, как если бы на каждую точку действовала сила 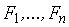. Для каждой материальной точки можно записать:

,

где 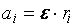, поэтому

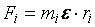, (1.7)

где m_i – масса i-й точки; 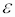– угловое ускорение; r_i – ее расстояние до оси вращения.

Умножая левую и правую части уравнения (1.7) на r_i, получают

, (1.8)

где 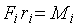– момент силы – это произведение силы на ее плечо .

Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы .

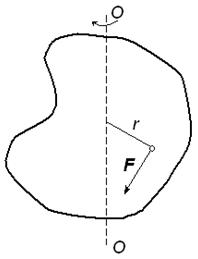
Рис. 5. Твердое тело, вращающееся под

действием силы F около оси “ОО”

– момент инерции i-й материальной точки.

Выражение (1.8) можно записать так:

. (1.9)

Просуммируем левую и правую части (1.9) по всем точкам тела:

.

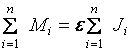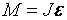Обозначим 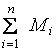через М, а 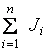через J, тогда

(1.10)

Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина 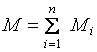– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорен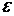ие . – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».

Мгновенное значение углового ускорения , есть первая производная угловой скорости 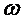по времени , то есть

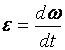, (1.11)

где – элементарное изменение угловой скорости тела за элементарный промежуток времени .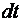

Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то

или 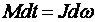, (1.12)

где – импульс момента силы – это произведение момента силы 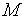на промежуток времени .

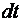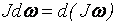– изменение момента импульса тела, – момент импульса тела есть произведение момента инерции J на угловую скорость 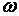, а есть .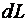

Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы 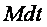, действующий на вращательное тело, равен изменению его момента импульса ”:

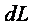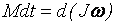или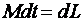

МАЯТНИК ОБЕРБЕКА

Цель работы – изучение основного закона динамики вращательного движения, определение момента инерции системы грузов.

Приборы и принадлежности: лабораторный модуль ЛКМ-3 со стойкой и блоком, стержень с отверстиями, два круглых груза, груз наборный, нить длиной 55 см с крючком (синяя), измерительная система ИСМ-1 (секундомер), пластиковый фиксатор.

Краткая теория

Основной закон динамики вращательного движения твердого тела относительно неподвижной оси

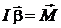(1)

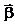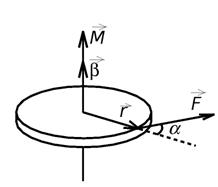
связывает кинематическую характеристику движения – угловое ускорение с динамическими характеристиками – моментом силы 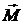и моментом инерции I (рис. 1).

Угловое ускорение характеризует изменение угловой скорости Рис. 1. Момент M силы F

во времени и направлено, как и момент силы, вдоль оси вращения. 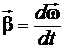(2) .

Угловое ускорение связано с касательной составляющей линейного ускорения а_τточки вращающегося тела соотношением

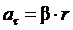, (3)

где r –- кратчайшее расстояние от этой точки до оси вращения.

Моментом силы в общем случае называют векторную величину

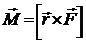, (4)

где 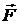– сила, лежащая в плоскости, перпендикулярной оси вращения; 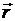– вектор, соединяющий точку на оси c точкой приложения силы.

В уравнении (1) 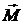– сумма составляющих моментов сил вдоль направления оси вращения.

Момент инерции I характеризует распределение массы в твердом теле относительно оси вращения и является мерой инертности вращающегося тела. Момент инерции равен сумме произведений элементарных масс Δm_i , на которые мысленно разбито тело, на квадрат их расстояний до оси вращения

I=ΣΔm_i r_{i .} (5)

Выражая Δm_i через плотность тела: Δm_i =ρ ΔV_i ,где ΔV_i – элементарный объем тела, и переходя к пределу при ΔV_i → 0, получим

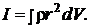(6)

Формула (6) позволяет теоретически найти момент инерции любого тела. Например, момент инерции тонкого однородного стержня длиной l и массой т относительно оси, проходящей перпендикулярно стержню через его центр,

I = т l ² / 12 .

Теорема Штейнера устанавливает связь между моментом инерции I_с твердого тела относительно оси, проходящей через центр инерции, и моментом инерции относительно другой оси, параллельной первой

I = I_с + та² , (7)

где а – расстояние между осями, т – масса тела.

В настоящей работе экспериментально находится момент инерции маятника Обербека (рис.2). Он состоит из блока радиусом R, который может вращаться вокруг неподвижной горизонтальной оси. К блоку прикреплены симметрично относительнооси стержни, на каждом из которых могут свободно перемещаться грузы массами m₁, что дает возможность изменять момент инерции маятника. Грузы m₁ устанавливаются на одинаковом расстоянии от оси, так что центр инерции всей вращающейся части маятника находится на оси вращения.

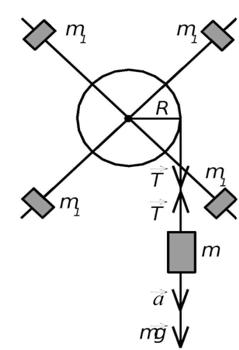
К концу нити прикреплен груз массой m. Из закона динамики вращательного движения следует

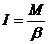. (8)

Момент силы М, создающийся силой натяжения нити, исходя из (4)

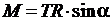, (9)

где α – угол между вектором 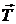и отрезком R на рис. 2, равный 90°; sin α= 1.

Запишем второй закон Ньютона для поступательного движения груза m в проекции на направление ускорения а,

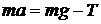. (10)

рис. 2. Маятник Обербека

В этой формуле сила натяжения нити T, действующая на груз, по модулю равна силе натяжения нити, действующей на блок в формуле (9) (поэтому они обозначены одинаково). Это справедливо, если массой нити можно пренебречь по сравнению с массой груза т.

Из (9) и (10) получим

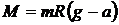. (11)

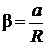Тангенциальное (касательное) ускорение точек участков нити, намотанной на блок, и точек на ободе блока равны, если нет проскальзывания нити по блоку, и равны ускорению груза m, если нить нерастяжима.

Тогда из (3) следует , (12)

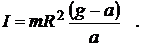(13)

Подставляя (11)и(12)в (8), получим

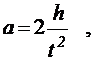Из этой формулы следует, что ускорение (а) не зависит от времени, так как все остальные величины в этом уравнении постоянны, значит, движение маятника будет равноускоренным и при нулевой начальной скорости.

(14)

где h – путь, пройденный грузом т за время t.

В данной работе измеряется время одного полного оборота блока, и за это время груз массой m пройдет путь

h=2πR . (15)

Подставив (14) и (15) в (13), получим формулу для вычисления момента инерции маятника

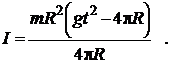
(16)

Момент инерции маятника Обербека будет изменяться при изменении расстояния r от оси вращения маятника до центров грузов массами m₁, перемещаемых вдоль стержней.

Согласно теореме Штейнера (7)

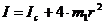, (17)

где I_c – момент инерции всей вращающейся части маятника при условии, что центры грузов m₁находились бы на оси вращения.

Из (17) следует, что зависимость 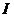от 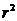– линейная. В рассмотренной теории движения маятника Обербека не учитывались силы трения в подшипниках оси блока и сопротивление воздуха. Пренебрежение действием этих сил является главной причиной систематической погрешности измерения момента инерции.