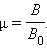Закон сохранения заряда в дифференциальной форме

Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)

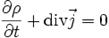
31. Электрическое поле в диэлектриках и проводниках.

Само собой разумеется, что электрическое поле может существовать не только в вакууме, но и внутри вещества, ибо электрические силы могут действовать и внутри различных тел. При этом, однако, надо иметь в виду существенное различие между проводниками и диэлектриками. В проводнике имеются электрические заряды, свободно перемещающиеся под действием электрических сил. В диэлектрике же движение зарядов под действием электрических сил происходить не может. Поэтому, если в проводнике возникло электрическое поле, то свободные заряды проводника придут в движение под действием этого поля, т. е. через проводник будет идти электрический ток.. Но в опытах с зарядкой отдельных проводников мы не наблюдаем длительного тока, т. е. заряды на проводнике после некоторых перемещений приходят в состояние равновесия. Равновесие будет достигнуто, когда заряды распределятся по проводнику таким образом, чтобы создаваемое ими внутри проводника электрическое поле как раз компенсировало внешнее поле, вызвавшее перемещение зарядов. Пока такая компенсация не наступила, электрические заряды, благодаря их подвижности в проводнике, будут продолжать движение. Таким образом, при равновесии зарядов напряженность электрического поля в проводнике равна нулю, т. е. электрическое поле в проводнике отсутствует.

В диэлектрике наличие электрического поля не препятствует равновесию зарядов. Сила, действующая на заряды в диэлектрике со стороны электрического поля, уравновешивается внутримолекулярными силами, удерживающими заряды в пределах молекулы диэлектрика, так что в диэлектрике возможно равновесие зарядов, несмотря на наличие электрического поля. Конечно, как мы уже указывали в § 3, разделение тел на проводники и диэлектрики условно. При достаточно большой напряженности поля и в диэлектрике возможно заметное перемещение зарядов, ведущее к пробою диэлектрика. Однако при общепринятом разделении тел на проводники и диэлектрики мы можем сказать, что в случае равновесия зарядов электрическое поле внутри проводника (например, металла) отсутствует, а электрическое поле в диэлектрике (например, в стекле) может существовать.
32. Магнетизм. Основные законы магнитного поля.

Магнети́зм — форма взаимодействия движущихся электрических зарядов, осуществляемая на расстоянии посредством магнитного поля. Наряду с электричеством, магнетизм — одно из проявлений электромагнитного взаимодействия. С точки зрения квантовой теории поля электромагнитное взаимодействие переносится безмассовым бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля).

Основные уравнения и законы

Современная теория магнетизма базируется на следующих основных уравнениях и законах:

§ Закон электромагнитной индукции Фарадея

§ Закон Ампера

§ Закон Био — Савара — Лапласа

§ Сила Лоренца

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в системе СИ):

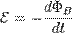
где

— электродвижущая сила, действующая вдоль произвольно выбранного контура,

— магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени российского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

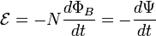
где

— электродвижущая сила,

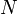— число витков,

— магнитный поток через один виток,

— потокосцепление катушки.

Зако́н Ампе́ра — закон взаимодействия постоянных токов.

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :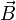

.

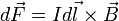Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поледействует на точечную заряженную частицу. Силой Лоренца называют иногда силу, действующую на движущийся со скоростью заряд 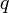лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1] иначе говоря, со стороны электрического и магнитного 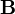полей в системе СИ:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом^[2].

Частным случаем силы Лоренца является сила Ампера.

33. Магнитное поле в веществе.

Магнитное поле в веществе

Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.

Физическая величина, показывающая, во сколько раз индукция 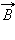магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.

Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо.Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).

Рисунок 1.19.1. Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле

Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным противнаправления индукции внешнего поля.

В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.

Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.

Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 10²–10⁵. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.

К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.

Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.

Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.

Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).

Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовления постоянных магнитов.

Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B₀внешнего поля. Типичная зависимость μ (B₀) приведена на рис. 1.19.2. В таблицах обычно приводятся значения максимальной магнитной проницаемости.

Рисунок 1.19.2. Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля

Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B₀ внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B₀) ферромагнитного образца представляет собой петлю сложной формы, которая называетсяпетлей гистерезиса (рис. 1.19.3).

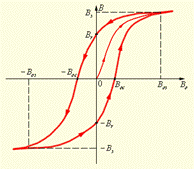Рисунок 1.19.3. Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B0 внешнего магнитного поля

Из рис. 1.19.3 видно, что при наступает магнитное насыщение – намагниченность образца достигает максимального значения.

Если теперь уменьшать магнитную индукцию B₀ внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно B_r. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B₀ до значения –B_0c, которое принято называть коэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 1.19.3.

У магнито-мягких материалов значения коэрцитивной силы B_0c невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.

Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка10^–2–10^–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.

В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. 1.19.4 может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.

Рисунок 1.19.4. Намагничивание ферромагнитного образца. (1) B0 = 0; (2) B0 = B01; (3) B0 = B02 > B01

34. Движение частиц в электрическом и магнитном полях.

Движение заряженных частиц

в

Однородном магнитном поле

Рассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0.

Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения. Прежде всего, отметим, что действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца

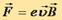
остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой. Но движение под действием постоянной по величине центростремительной силы есть движение по окружности. Радиус r этой окружности определяется условием

откуда

Если энергия электрона выражена в эВ и равна U, то

(3.6)

и поэтому

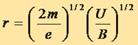
Кругообразное движение заряженных частиц в магнитном поле обладает важной особенностью: время полного обращения частицы по окружности (период движения) не зависит от энергии частицы. Действительно, период обращения равен

Подставляя сюда вместо r его выражение по формуле (3.6), имеем:

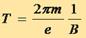(3.7)

Частота же оказывается равной

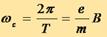
Для данного типа частиц и период, и частота зависят только от индукции магнитного поля.

Выше мы предполагали, что направление начальной скорости перпендикулярно к направлению магнитного поля. Нетрудно сообразить, какой характер будет иметь движение, если начальная скорость частицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью

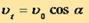
В результате сложения обоих движений частица будет двигаться по цилиндрической спирали.

Шаг винта этой спирали равен

подставляя вместо T его выражение (3.7), имеем:

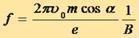
Движение заряженных частиц

в

Неоднородном магнитном поле

В неоднородном магнитном поле движение частиц усложняется. Пусть мгновенная скорость частицы перпендикулярна плоскости чертежа. Тогда составляющая индукции B1 обеспечит силу F движение частицы по окружности.

Составляющая B2 создает силу F', выталкивающую частицу в область слабого поля. Так как сила Лоренца не совершает работы, то при этом сложном движении сохраняются две величины:

а) полная кинетическая энергия частицы, что при малых скоростях равносильно сохранению модуля полной скорости;

б) магнитный поток Ф через плоскость орбиты частицы, так как всякое изменение его связано с совершением работы, где i - сила тока, эквивалентного движущейся частице

Решая уравнение 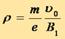относительно скорости частицы и умножал его на , получаем

Таким образом, произведение радиуса окружности на скорость движения частицы по окружности (окружную скорость) сохраняется неизменным.

При перемещении частицы в область слабого поля радиус p растет, а скорость U0 соответственно уменьшается. Поэтому увеличивается составляющая полной скорости, направленная по оси винтовой линии, описываемой частицей, то есть увеличивается расстояние между расширяющимися витками винтовой линии. Если же частица в некоторый момент обладала скоростью , причем 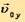- окружная скорость, а 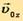скорость, направленная в сторону возрастания индукции B то винтовая линия, описываемая частицей, будет состоять из сближающихся витков уменьшающегося радиуса, а составляющая скорости будет стремиться к нулю.

Проникнув в область сильного поля, частица станет обращаться по окружности постоянного радиуса. Однако такое состояние неустойчиво, так как внутри окружности индукция собственного магнитного поля, создаваемого частицей, направлена против индукции внешнего поля.

Поэтому частица, не проникнув в область слишком сильного поля индукции B начнёт выталкиваться в область слабого поля.

Именно такой эффект проявляется в магнитном поле Земли, захватывающем заряженные частицы, приходящие из космоса, в частности от Солнца. Эти частицы образуют вокруг Земли заряженные слои (радиационные пояса).

Движение заряженных частиц

в