Равновесие в системе, состоящей из большого числа частиц.
Релаксация (от лат. relaxatio — ослабление, уменьшение) — процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.
Релаксация — многоступенчатый процесс, так как не все физические параметры системы (распределение частиц по координатам и импульсам, температура, давление, концентрация в малых объёмах и во всей системе и другие) стремятся к равновесию с одинаковой скоростью. Обычно сначала устанавливается равновесие по какому-либо параметру (частичное равновесие), что также называется релаксацией. Все процессы релаксации являются неравновесными процессами, при которых в системе происходит диссипация энергии, то есть производится энтропия (в замкнутой системе энтропия возрастает). В различных системах релаксацияимеет свои особенности, зависящие от характера взаимодействия между частицами системы; поэтому процессы релаксации весьма многообразны. Время установления равновесия (частичного или полного) в системе называется временем релаксации. Процесс установления равновесия в газах определяется длиной свободного пробега частиц 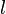 и временем свободного пробега
и временем свободного пробега 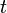 (среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение
(среднее расстояние и среднее время между двумя последовательными столкновениями молекул). Отношение 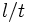 имеет порядок величины скорости частиц. Величины
имеет порядок величины скорости частиц. Величины 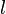 и
и 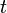 очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения
очень малы по сравнению с макроскопическими масштабами длины и времени. С другой стороны, для газов время свободного пробега значительно больше времени столкновения 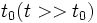 . Только при этом условиирелаксация определяется лишь парными столкновениями молекул.
. Только при этом условиирелаксация определяется лишь парными столкновениями молекул.
Для одноатомных газов
В одноатомных газах (без внутренних степеней свободы, то есть обладающих только поступательными степенями свободы)релаксация происходит в два этапа.
На первом этапе за короткий промежуток времени, порядка времени столкновения молекул то, начальное, даже сильно неравновесное, состояние хаотизируется таким образом, что становятся несущественными детали начального состояния и оказывается возможным так называемое «сокращённое описание» неравновесного состояния системы, когда не требуется знания вероятности распределения всех частиц системы по координатам и импульсам, а достаточно знать распределение одной частицы по координатам и импульсам в зависимости от времени, то есть одночастичную функцию распределения молекул. (Все остальные функции распределения более высокого порядка, описывающие распределения по состояниям двух, трёх и т. д. частиц, зависят от времени лишь через одночастичную функцию). Одночастичная функция удовлетворяет кинетическому уравнению Больцмана, которое описывает процесс релаксации. Этот этап называется кинетическим и является очень быстрым процессом релаксации.
На втором этапе за время порядка времени свободного пробега молекул и в результате всего нескольких столкновений в макроскопически малых объёмах системы устанавливается локальное равновесие; ему соответствует локально-равновесное, или квазиравновесное, распределение, которое характеризуется такими же параметрами, как и при полном равновесии системы, но зависящими от пространственных координат и времени. Эти малые объёмы содержат ещё очень много молекул, а поскольку они взаимодействуют с окружением лишь на своей поверхности, их можно считать приближённо изолированными. Параметры локально-равновесного распределения в процессе релаксации медленно стремятся к равновесным, а состояние системы обычно мало отличается от равновесного. Время релаксации для локального равновесия 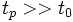 . После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса,уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время
. После установления локального равновесия для описания релаксации неравновесного состояния системы служат уравнения гидродинамики (уравнения Навье — Стокса,уравнения теплопроводности, диффузии и т. п.). При этом предполагается, что термодинамические параметры системы (плотность, температура и т. д.) и массовая скорость (средняя скорость переноса массы) мало меняются за время 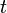 и на расстоянии
и на расстоянии 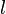 . Этот этапрелаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
. Этот этапрелаксации называется гидродинамическим. Дальнейшая релаксация системы к состоянию полного статистического равновесия, при котором выравниваются средние скорости частиц, средняя температура, средняя концентрация и т. д., происходит медленно в результате очень большого числа столкновений.
Такие процессы (вязкость, теплопроводность, диффузия, электропроводность и т. п.) называются медленными. Соответствующее время релаксации 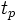 зависит от размеров
зависит от размеров 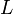 системы и велико по сравнению с
системы и велико по сравнению с 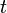 :
: 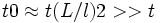 , что имеет место при
, что имеет место при 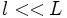 , то есть для не сильно разреженных газов.
, то есть для не сильно разреженных газов.
Для многоатомных газов
В многоатомных газах (с внутренними степенями свободы) может быть замедлен обмен энергией между поступательными и внутренними степенями свободы, и возникает процесс релаксации, связанный с этим явлением. Быстрее всего — за время порядка времени между столкновениями — устанавливается равновесие по поступательным степеням свободы; такое равновесное состояние можно охарактеризовать соответствующей температурой. Равновесие между поступательными и вращательными степенями свободы устанавливается значительно медленнее. Возбуждение колебательных степеней свободы может происходить лишь при высоких температурах. Поэтому в многоатомных газах возможны многоступенчатые процессы релаксации энергии колебательных и вращательных степеней свободы.
Для смесей газов
В смесях газов с сильно различающимися массами молекул замедлен обмен энергией между компонентами, вследствие чего возможно возникновение состояния с различными температурами компонент и процессы релаксации их температур. Например, вплазме сильно различаются массы ионов и электронов. Быстрее всего устанавливается равновесие электронной компоненты, затем приходит в равновесие ионная компонента, и значительно большее время требуется для установления равновесия между электронами и ионами; поэтому в плазме могут длительное время существовать состояния, в которых ионные и электронные температуры различны а, следовательно, происходят процессы релаксации температур компонент.
Для жидкостей
В жидкостях теряет смысл понятие времени и длины свободного пробега частиц (а следовательно, и кинетического уравнения для одночастичной функции распределения). Аналогичную роль для жидкости играют величины 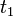 и
и 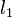 — время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1 и l1 характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксациии локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции
— время и длина корреляции динамических переменных, описывающих потоки энергии или импульса; t1 и l1 характеризуют затухание во времени и в пространстве взаимного влияния молекул, то есть корреляции. При этом полностью остаётся в силе понятие гидродинамического этапа релаксациии локально-равновесного состояния. В макроскопически малых объёмах жидкости, но ещё достаточно больших по сравнению с длиной корреляции 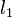 , локально-равновесное распределение устанавливается за время порядка времени корреляции
, локально-равновесное распределение устанавливается за время порядка времени корреляции 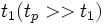 в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время
в результате интенсивного взаимодействия между молекулами (а не парных столкновений, как в газе), но эти объёмы по-прежнему можно считать приближённо изолированными. На гидродинамическом этапе релаксация в жидкости термодинамические параметры и массовая скорость удовлетворяют таким же уравнениям гидродинамики, как и для газов (при условии малости изменения термодинамических параметров и массовой скорости за время 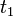 и на расстоянии
и на расстоянии 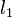 ). Время релаксациик полному термодинамическому равновесию
). Время релаксациик полному термодинамическому равновесию 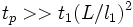 (так же, как в газе и твёрдом теле) можно оценить с помощьюкинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме
(так же, как в газе и твёрдом теле) можно оценить с помощьюкинетических коэффициентов. Например, время релаксации концентрации в бинарной смеси в объёме 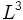 порядка
порядка 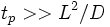 , где
, где 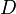 — коэффициент диффузии, время релаксации температуры
— коэффициент диффузии, время релаксации температуры 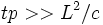 , где
, где  — коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
— коэффициент температуропроводности, и т. д. Для жидкости с внутренними степенями свободы молекул возможно сочетание гидродинамического описания поступательных степеней свободы с дополнительными уравнениями для описания релаксации внутренних степеней свободы (релаксационная гидродинамика).
22. Второе начало термодинамики. Термодинамическое определение энтропии.
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.
Другая формулировка второго начала термодинамики основывается на понятии энтропии:
§ «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).
Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамикеявляется функцией состояния термодинамической системы.
