Потенциальная энергия гравитационного взаимодействия и упругой деформации.

Скорость

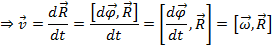
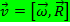
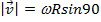
Ускорение

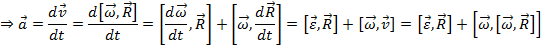
По касательной траектории в данной ее точке 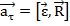Þ a_t = eRsin90^o = eR

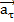называется касательноым ускорением, характеризующим изменение скорости по величине

По нормальной траектории в данной ее точке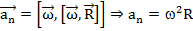

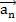называются тангенциальным ускорением, характеризующим изменение скорости по направлению

Тогда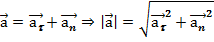

Границы применимости классического способа описания движения точки:

Все вышеизложенное относится к классическому способу описания движения м. точки. В случае неклассического рассмотрения движения микрочастиц понятия траектории их движения не существует, но можно говорить о вероятности нахождения частицы в той или иной области пространства. Для микрочастицы нельзя одновременно указать точные значения координаты и скорости. В квантовой механике существует соотношение неопределенностей

В. Гайзенберга 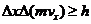, где h=1,05∙10^-34 Дж∙с (постоянная Планка), которое определяет погрешности одновременного измерения координаты 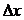и импульса

3) Динамика материальной точки. Масса. Сила. Инерциалные системы отсчета. Законы Ньютона.

Динамика– это раздел физики, изучает движение тел в связи с причиами, возврающыми тот или силой характер движения

Масса — физическая величина, отвечающая способности физических тел сохранять своё поступательное движение (инертности), а также характеризующая количество вещества

Сила– мера взаймодецствие между телами.

Инерциалные системы отсчета: Существуют такие системы отсчета относителього, которых тело находится в состоянии покоя (движится равно прямо линии) до тех пор пока на него не подействуют другие тела.

Система отсчета – инерциальный: любая другая движения относительно гелиоцентризм равномерно и прямо, так же является инерциальной.

Инерция – это явление связанное с способностьб тел сохранять свою скорость.

Инертность – способность материального тела сокрашать свою скорость. Чем более инертно тело, тем “Труднее” изменить его v. Количественной мерой инертности является масса тела, как мера инертность тела.

Законы Ньютона

Й закон Ньютона.

Существуют такие системы отсчета, называемые инерциальными системами, в которых материалтная точка находится в состоянии нии покоя или равномерного прчмолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния.

Й закон Ньютона.

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.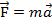

3-й закон Ньютона:силы, с которыми две м. точки действуют друг на друга в ИСО, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.

1) Если на тело А действует сило со стороны тело В, то на тело В действует сила А. Эти силы F₁₂ и F₂₁ имеют одинаковую физическую природу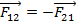

2) Сила взаимодействуют между телами, не зависит от скорости движения тел

4) Система материальных точек. Внутренние и внешние силы. Импульс материальной точки и импульс системы материальных точек. Закон сохранения импульса. Условия его применимости закона сохранения импульса. Преобразования Галилея, принцип относительно Галилея

Cистема материальных точек: это такая система содержится точкими, который жестко связанных друг с другом.

Внутренние силы:Силы взаимодействия между точками системы называется внутренными силами

Внешние силы: Силы взаимодействуют на точки системы со стороны тел, не входящих в системе называется внешними силами.

Система называется замкнутой системой, если на тела системы не действует внешние силы.

Импульс материальной точкиназываетсяпроизведением массы на скорость точки 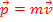Импульс системы материальных точек: Импульс системы материальных точек равен произведением массы системы на скорость движения ценрта масс.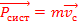

Закон сохранения импульса: Для замкнутой системы взаимодействует тел суммарный импульс системы остается неизменным, независимо от любых взаимодействующих тел между собой

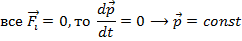
Условия его применимости закона сохранения импульса:Закон сохранения импульса можно использовать при замкнутых условиях, даже если система не замкнута.

1)

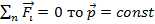
2)

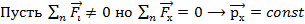
3)

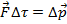
Если 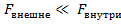и при этом 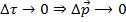следовательно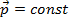

Закон сохранения импульса работает и в микромере, когда классическая механика не работает, импульс сохраняется.

Преобразования Галилея, принцип относительно Галилея

Пусть имеем 2 инерциальные системы отсчета, одна из которых движется относительно второй, с постоянной скоростью v_o . Тогда в соотвеств с преобразованием Галилея ускорение тела в оба систем отсчета окажется одинаковым.

1) Равномерное и прямолинецное движение системы не влияет на ход протекающих в них механических процессов.

2) Все инерциальные системы поставим свойством эквиваленно друг другу.

3) Никакими механическими опытами внутри системы невозможноустановаить покоиться система или движется равномерно или прямолинейно.

Относительность механического движения и одинаковость законов механики в разных инерциальных системах отсчета называется принципом относительности Галилея

5) Система материальных точек. Центр масс системы материальных точек. Теорема о движении центра масс системы материальных точек.

Любое тело можно представить как совокупность материальных точек.

Пусть имеет систему материальных точек массами m₁, m₂,…,m_i, положения которыз относительно инерциальной системе отсчета характеризуется векторами соотвестенно 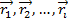, тогда по определению положение центра масс системы материальных точек определяется выражением: .

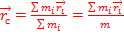Где 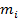масса i – той частицы

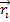– характеризует положение этой частицы относительно заданной системы координат,

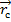– характеризуетс полодение центра масс системы относительно той же системы координат.

Скорость цетра масс

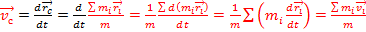
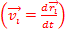
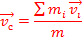
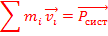
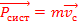
Импульс системы материальных точек равен произвоеденнию массы системы на скорость движения ценрта масс.

Если 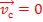то система мы говорим, что система как центр покоится.

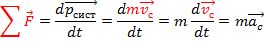
1) Центр масс системы движения так, если бы вся масса системы была сосредоточена в центре масс, а все силы действуют на тела системы ыли приложеие к центру масс.

2) Ускорение центра масс не зависит от точек приложения сил, действующих на тело системы.

3) Если 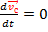( ускорение = 0 ) то импульс системы не изменияется.

6) Работа в механике. Понятие поля сил. Потенциальные и непотенциальные силы. Критерий потенциальности сил поля.

Работа в механике: Работой силы F на элемент перемещение 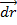называется скалярное произведение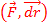

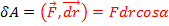
Работа – величина алгеброическая ( )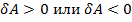

Понятие поля сил: Если в каждой материальной точке постранства на тело действуют определенная сила, то говорят, что тело находится в поле сил.

Потенциальные и непотенциальные силы, критерий потенциальности сил поля:

С точки зрения производшией работы будет размечать потенциальные и непотенциальные телы. Силы, для каждых:

1) Работа не зависит от формы траектории, а зависит лишь от начального и кнечного положения тела.

2) Работа, которая по замкнутым траекториям равно нулью, называется потенциальнями.

Силы удоблы этим условиям называется потенциалтными.

Силы не удоблы этим условиям называется непотенциалтными.

К первым относится 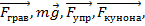и только отной силой трения 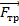непотенциально.

7) Кинетическая энергия материальной точки, системы материальных точек. Теорема об изменении кинетической энергии.

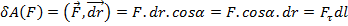
Но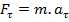

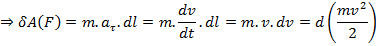
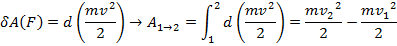
Комплекс: 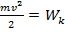называется кинетической энергией.

Тогда 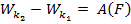Где 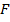внешние сило

Теорема об изменении кинетической энергии: изменение кин. энергии м. точки равно алгебраической сумме работ всех приложенных к ней сил.

Если на тело одновременно действуют несколько внешние сил то изменение крнетической энергии равно “ аллебраической работе” всех сил, действуют на тело: 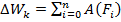эта формула теоремы кинетической кинетики.

Кин. энергией системы тел наз. сумма кин. энергий всех тел, входящих в эту систему.

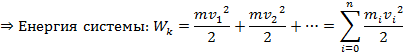
8) Потенциальная энергия. Изменение потенциальной энергии. Потенциальная энергия гравитационного взаимодействия и упругой деформации.

Потенциальная энергия 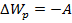– физическая виличина, изменение которой равно работе потенциальной силе системы взятой с знаком “-”.

Введем некоторую функцию W_p , являющуюся потенциальной энергией f(x,y,z), которую определим следующим образом

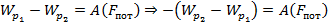
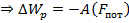
Знак “-” показывает, что при совершении работы этой потециалной силой, потециальная энергия уменьшается.

Изменение потенциальной энергии системы тел, между которыми действуют только потенциальные силы, равно взятой с обратным знаком работе этих сил при переходе системы из одного состояния в другое.

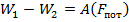
Уравнение моментов

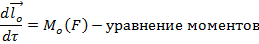
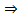Производная момента импульса материальной точки оносительно неподвижной оси по времени равна момент сила действуйщий на точку относително той же ось.

Суммарно всех внутренных сил относително в любой точки равно нулью. Поэтому

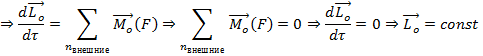
Термический коэффициент полезного действия (КПД) цикла Тепловая машина.

Мерой эффективности преобразования теплоты, подведенной количество рабочему телу, в работу тепловой машины над внешними телами является коэффициент полезного действиятепловой машины

Теродинамический КРД:

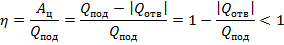
Тепловая машина: при превращении тепловой энергии в механическую работу. Основный элемент тепловой машины работа тел.

Q_под

Q_отв

Энергический цикл

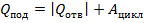
Холодильная машина.

26) Цикл Карно, КПД цикла Карно. Второе начато термодинамики. Его различные
формулировки.

Цикл Карно: это цикл состоит из двух изотермических процесов и из двух адиабаты.

1-2: Изотермический процесс расширении газа при температуре нагревателя Т₁ и подводит тепло.

2-3: Адиабатический процесс расширении газа при этом температура понижается от Т₁ до Т₂.

3-4: Изотермический процесс сжимании газа при этом отводится тепла и температура равна Т₂

4-1: Адиабатический процесс сжимании газа при этом температура газа развивает от холодильника до нагревателя.

Сказывается для цикла Карно, общем вражения КПД существует производитель

В теоретическом смысле, этот цикл будет максимальным среди возможно КПДдля всех циклов, работающих между температурами Т₁ и Т₂.

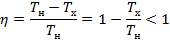
Теорима Карно: Коэффициент полезной мощности теплового цикла Карно не зависит от вида работика дело и устойства самой машины. А только определятся температурами Т_н и T_х

Второе начато термодинамики

Второй закон термоднамики определяет направление протекания тепловых машин. Нелзья построить термодинамический цикл, действющий тепловой машин без холодильника. При этом цикле энергия системы ввидит ….

В этом случае КПД

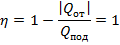
Его различные формулировки.

1) Первая формулировка: “Томсона”

Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела.

2) Вторая формулировка: “Клаузиса”

Невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему.

27) Энтропия - функция состояния термодинамической системы. Расчет изменения энтропии в процессах идеального газа. Неравенство Клаузиуса. Основное свойство энтропии (формулировка второго начала термодинамики через энтропию). Статистический смысл второго начала.

Неравенство Клаузиуса

Исходное условие второй закон термодинамики, Клаузиуса было получено соотношение

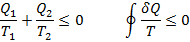
Знак равенство соотвествено обратимого цикла и процесса.

Наиболее вероятная

Скоростью молекул соотвествено максимальное значение функции распределения называется наивернейшая вероятность.

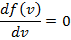
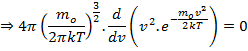
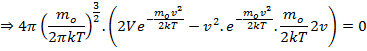
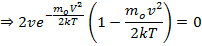
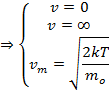
Постулаты Эйнштейна

1) Принцип относительности Эйнштейна: все физические законы одинаковы во всех инерциальных системах отсчета, а поэтому они должны быть сформулированы в виде, инвариантном относительно преобразований координат, отражающих переход от одной ИСО к другой.

2) 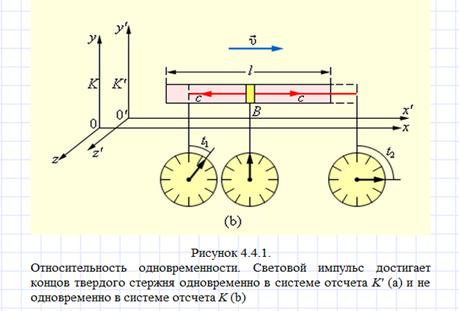Принцип постоянства скорости света: существует предельная скорость распространения взаимодействиий, величина которой во всех ИСО одинакова и равна скорости электромагнитной волны в вакууме и не зависит ни от направления ее распространения, не от движения источника и приемника.

Следствия из преобразований Лоренца

Лоренцево сокращение длины

Рассмотрим стержень, расположенный вдоль оси ОХ’ системы (Х’,Y’,Z’) и неподвижный относительно этой системы координат. Собственнoй длиной стержняназывается величина 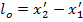то есть длина, измеренная в ситеме отсчета (X,Y,Z) будет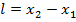

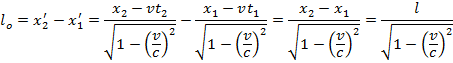
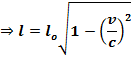
Следовательно, наблюдатель в системе (X,Y,Z) находит, что лина движущегося стержня в 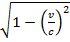раз меньше собственной длины.

34) Релятивистская динамика. Второй закон Ньютона применительно к большим
скоростям. Релятивистская энергия. Связь массы и энергии.

Релятивистская динамика

Связь импульса частицы с её скоpостью тепеpь задается

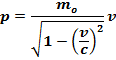
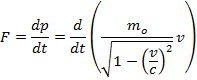
Релятивистская энергия

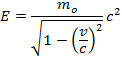
Покоящаяся частица обладает энергией

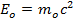
Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

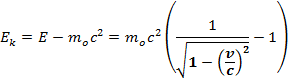
Связь массы и энергии

Полная энергия

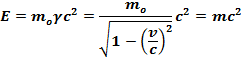
Поскольку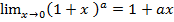

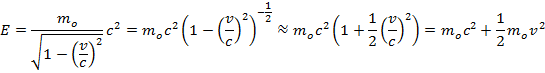
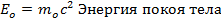
Скорость

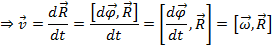
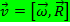
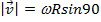
Ускорение

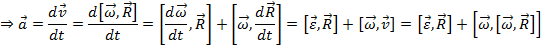
По касательной траектории в данной ее точке 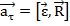Þ a_t = eRsin90^o = eR

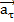называется касательноым ускорением, характеризующим изменение скорости по величине

По нормальной траектории в данной ее точке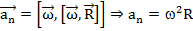

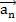называются тангенциальным ускорением, характеризующим изменение скорости по направлению

Тогда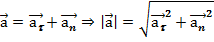

Границы применимости классического способа описания движения точки:

Все вышеизложенное относится к классическому способу описания движения м. точки. В случае неклассического рассмотрения движения микрочастиц понятия траектории их движения не существует, но можно говорить о вероятности нахождения частицы в той или иной области пространства. Для микрочастицы нельзя одновременно указать точные значения координаты и скорости. В квантовой механике существует соотношение неопределенностей

В. Гайзенберга 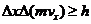, где h=1,05∙10^-34 Дж∙с (постоянная Планка), которое определяет погрешности одновременного измерения координаты 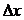и импульса

3) Динамика материальной точки. Масса. Сила. Инерциалные системы отсчета. Законы Ньютона.

Динамика– это раздел физики, изучает движение тел в связи с причиами, возврающыми тот или силой характер движения

Масса — физическая величина, отвечающая способности физических тел сохранять своё поступательное движение (инертности), а также характеризующая количество вещества

Сила– мера взаймодецствие между телами.

Инерциалные системы отсчета: Существуют такие системы отсчета относителього, которых тело находится в состоянии покоя (движится равно прямо линии) до тех пор пока на него не подействуют другие тела.

Система отсчета – инерциальный: любая другая движения относительно гелиоцентризм равномерно и прямо, так же является инерциальной.

Инерция – это явление связанное с способностьб тел сохранять свою скорость.

Инертность – способность материального тела сокрашать свою скорость. Чем более инертно тело, тем “Труднее” изменить его v. Количественной мерой инертности является масса тела, как мера инертность тела.

Законы Ньютона

Й закон Ньютона.

Существуют такие системы отсчета, называемые инерциальными системами, в которых материалтная точка находится в состоянии нии покоя или равномерного прчмолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния.

Й закон Ньютона.

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение.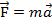

3-й закон Ньютона:силы, с которыми две м. точки действуют друг на друга в ИСО, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.

1) Если на тело А действует сило со стороны тело В, то на тело В действует сила А. Эти силы F₁₂ и F₂₁ имеют одинаковую физическую природу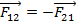

2) Сила взаимодействуют между телами, не зависит от скорости движения тел

4) Система материальных точек. Внутренние и внешние силы. Импульс материальной точки и импульс системы материальных точек. Закон сохранения импульса. Условия его применимости закона сохранения импульса. Преобразования Галилея, принцип относительно Галилея

Cистема материальных точек: это такая система содержится точкими, который жестко связанных друг с другом.

Внутренние силы:Силы взаимодействия между точками системы называется внутренными силами

Внешние силы: Силы взаимодействуют на точки системы со стороны тел, не входящих в системе называется внешними силами.

Система называется замкнутой системой, если на тела системы не действует внешние силы.

Импульс материальной точкиназываетсяпроизведением массы на скорость точки 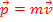Импульс системы материальных точек: Импульс системы материальных точек равен произведением массы системы на скорость движения ценрта масс.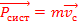

Закон сохранения импульса: Для замкнутой системы взаимодействует тел суммарный импульс системы остается неизменным, независимо от любых взаимодействующих тел между собой

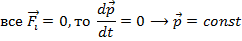
Условия его применимости закона сохранения импульса:Закон сохранения импульса можно использовать при замкнутых условиях, даже если система не замкнута.

1)

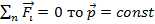
2)

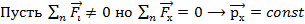
3)

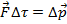
Если 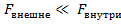и при этом 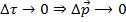следовательно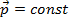

Закон сохранения импульса работает и в микромере, когда классическая механика не работает, импульс сохраняется.

Преобразования Галилея, принцип относительно Галилея

Пусть имеем 2 инерциальные системы отсчета, одна из которых движется относительно второй, с постоянной скоростью v_o . Тогда в соотвеств с преобразованием Галилея ускорение тела в оба систем отсчета окажется одинаковым.

1) Равномерное и прямолинецное движение системы не влияет на ход протекающих в них механических процессов.

2) Все инерциальные системы поставим свойством эквиваленно друг другу.

3) Никакими механическими опытами внутри системы невозможноустановаить покоиться система или движется равномерно или прямолинейно.

Относительность механического движения и одинаковость законов механики в разных инерциальных системах отсчета называется принципом относительности Галилея

5) Система материальных точек. Центр масс системы материальных точек. Теорема о движении центра масс системы материальных точек.

Любое тело можно представить как совокупность материальных точек.

Пусть имеет систему материальных точек массами m₁, m₂,…,m_i, положения которыз относительно инерциальной системе отсчета характеризуется векторами соотвестенно 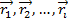, тогда по определению положение центра масс системы материальных точек определяется выражением: .

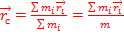Где 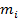масса i – той частицы

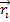– характеризует положение этой частицы относительно заданной системы координат,

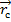– характеризуетс полодение центра масс системы относительно той же системы координат.

Скорость цетра масс

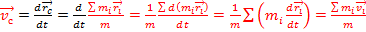
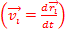
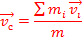
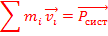
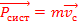
Импульс системы материальных точек равен произвоеденнию массы системы на скорость движения ценрта масс.

Если 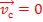то система мы говорим, что система как центр покоится.

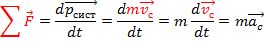
1) Центр масс системы движения так, если бы вся масса системы была сосредоточена в центре масс, а все силы действуют на тела системы ыли приложеие к центру масс.

2) Ускорение центра масс не зависит от точек приложения сил, действующих на тело системы.

3) Если 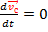( ускорение = 0 ) то импульс системы не изменияется.

6) Работа в механике. Понятие поля сил. Потенциальные и непотенциальные силы. Критерий потенциальности сил поля.

Работа в механике: Работой силы F на элемент перемещение 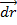называется скалярное произведение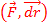

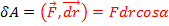
Работа – величина алгеброическая ( )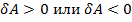

Понятие поля сил: Если в каждой материальной точке постранства на тело действуют определенная сила, то говорят, что тело находится в поле сил.

Потенциальные и непотенциальные силы, критерий потенциальности сил поля:

С точки зрения производшией работы будет размечать потенциальные и непотенциальные телы. Силы, для каждых:

1) Работа не зависит от формы траектории, а зависит лишь от начального и кнечного положения тела.

2) Работа, которая по замкнутым траекториям равно нулью, называется потенциальнями.

Силы удоблы этим условиям называется потенциалтными.

Силы не удоблы этим условиям называется непотенциалтными.

К первым относится 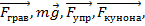и только отной силой трения 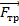непотенциально.

7) Кинетическая энергия материальной точки, системы материальных точек. Теорема об изменении кинетической энергии.

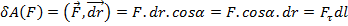
Но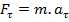

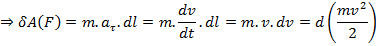
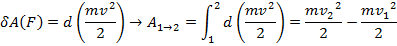
Комплекс: 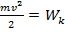называется кинетической энергией.

Тогда 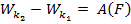Где 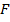внешние сило

Теорема об изменении кинетической энергии: изменение кин. энергии м. точки равно алгебраической сумме работ всех приложенных к ней сил.

Если на тело одновременно действуют несколько внешние сил то изменение крнетической энергии равно “ аллебраической работе” всех сил, действуют на тело: 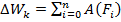эта формула теоремы кинетической кинетики.

Кин. энергией системы тел наз. сумма кин. энергий всех тел, входящих в эту систему.

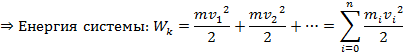
8) Потенциальная энергия. Изменение потенциальной энергии. Потенциальная энергия гравитационного взаимодействия и упругой деформации.

Потенциальная энергия 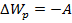– физическая виличина, изменение которой равно работе потенциальной силе системы взятой с знаком “-”.

Введем некоторую функцию W_p , являющуюся потенциальной энергией f(x,y,z), которую определим следующим образом

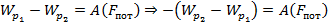
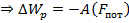
Знак “-” показывает, что при совершении работы этой потециалной силой, потециальная энергия уменьшается.

Изменение потенциальной энергии системы тел, между которыми действуют только потенциальные силы, равно взятой с обратным знаком работе этих сил при переходе системы из одного состояния в другое.

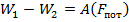
Потенциальная энергия гравитационного взаимодействия и упругой деформации.

1) Гравитационная сила

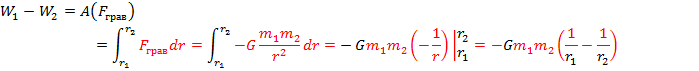
2) Работа силя упругости

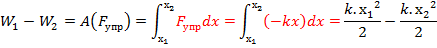
9) Дефференциальная связь между потенциальной силой и потенциальной энергией. Градиент скалярного поля.

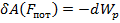
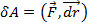
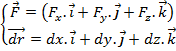
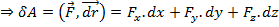
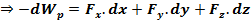
Пусть перемещение только вдоль оси х

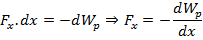
Аналогично, пусть перемещение только вдоль оси у или z, мы получили

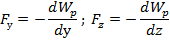
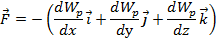
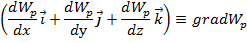
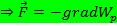
Знак “-” в формуле показывает что, силы всегда напровление в сторону поменьщается потенциальной энергии, но противно градиент W_p.

Геометрическая смысль точек с одинаковыи значением потенциальной энергии называется эквипотенциальная поверхность.

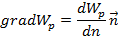
10) Закон сохранения энергии. Абсолютно не упругий и абсолютно упругий центральные удары шаров.

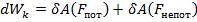
Но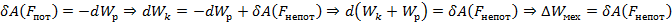

Изменение механической энергии системы равно сумме работы всех непотенциалтных сил внутрен иак и внешние.

*) Закон сохранения механической энергии : Механическая энергия системы сохраняется если работаы всех непотенциальных сил (как внутренние так и внешние) равно нулью.

При этом возможно слишь переход потенциальной энергии в кинетическую энергию и наоборот польная энергия постояно: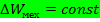

*)Общий физический закон сохранения энергии:Энергия на создается и не уничтожается, она либо переходит из первого виды в другой состоянии.